A man wishes to swim across a river 40 m wide flowing with a speed of 3m/s. such that he reaches the point just infront on the other bank in time not greater than 10s. The angle made by the direction he swims and river flow direction is :-
90∘
127∘
150∘
143∘
The correct Answer is:B
To solve the problem, we need to determine the angle made by the direction the man swims and the river flow direction. Let's break down the solution step by step.
Step 1: Understand the problem
The river is 40 meters wide and flows with a speed of 3 m/s. The swimmer wants to reach directly across the river in a time not greater than 10 seconds.
Step 2: Identify the components of motion
Let:
- v = speed of the swimmer
- θ = angle made by the swimmer's direction with the river flow direction
- vx=vcosθ = horizontal component of the swimmer's speed
- vy=vsinθ = vertical component of the swimmer's speed
Step 3: Set up the equations
1. The swimmer must reach the opposite bank in 10 seconds. The width of the river is 40 m, so:
vy⋅t=40(1)
Substituting t=10 seconds:
vsinθ⋅10=40⟹vsinθ=4(2)
2. To reach directly across without drifting downstream, the horizontal component of the swimmer's speed must equal the speed of the river:
vx=vcosθ=3(3)
Step 4: Solve the equations
Now we have two equations:
1. vsinθ=4
2. vcosθ=3
Dividing equation (2) by equation (3):
vsinθvcosθ=43
This simplifies to:
tanθ=43
Step 5: Calculate the angle
To find θ:
θ=tan−1(43)
Calculating this gives:
θ≈53∘
Step 6: Determine the angle with respect to the river flow
Since the angle made by the direction he swims and the river flow direction is θ, we need to find the angle α that is complementary to θ:
Angle with respect to river flow=180∘−θ
Thus:
Angle=180∘−53∘=127∘
Final Answer
The angle made by the direction he swims and the river flow direction is 127∘.
---
The river is 40 meters wide and flows with a speed of 3 m/s. The swimmer wants to reach directly across the river in a time not greater than 10 seconds.
Let:
- v = speed of the swimmer
- θ = angle made by the swimmer's direction with the river flow direction
- vx=vcosθ = horizontal component of the swimmer's speed
- vy=vsinθ = vertical component of the swimmer's speed
1. The swimmer must reach the opposite bank in 10 seconds. The width of the river is 40 m, so:
vy⋅t=40(1)
Substituting t=10 seconds:
vsinθ⋅10=40⟹vsinθ=4(2)
vx=vcosθ=3(3)
Now we have two equations:
1. vsinθ=4
2. vcosθ=3
vsinθvcosθ=43
This simplifies to:
tanθ=43
To find θ:
θ=tan−1(43)
Calculating this gives:
θ≈53∘
Since the angle made by the direction he swims and the river flow direction is θ, we need to find the angle α that is complementary to θ:
Angle with respect to river flow=180∘−θ
Thus:
Angle=180∘−53∘=127∘
The angle made by the direction he swims and the river flow direction is 127∘.
Topper's Solved these Questions
Similar Questions
A man wishes to swim across a river 0.5km. wide if he can swim at the rate of 2 km/h. in still water and the river flows at the rate of 1km/h. The angle (w.r.t. the flow of the river) along which he should swin so as to reach a point exactly oppposite his starting point, should be:-
View SolutionA man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5sec. his velocity in still water should be
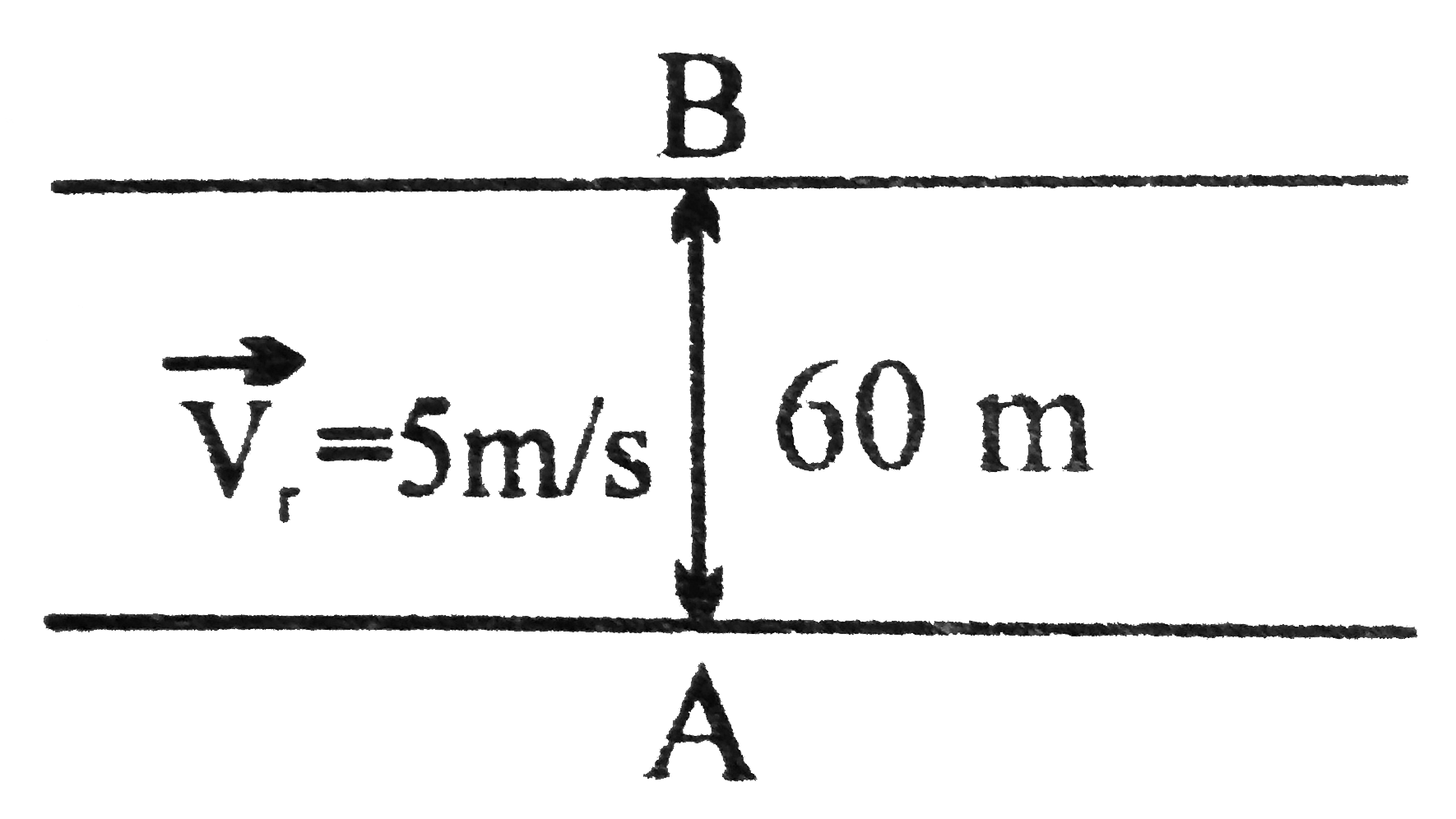
View SolutionA man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5 sec. His velocity in still water should be
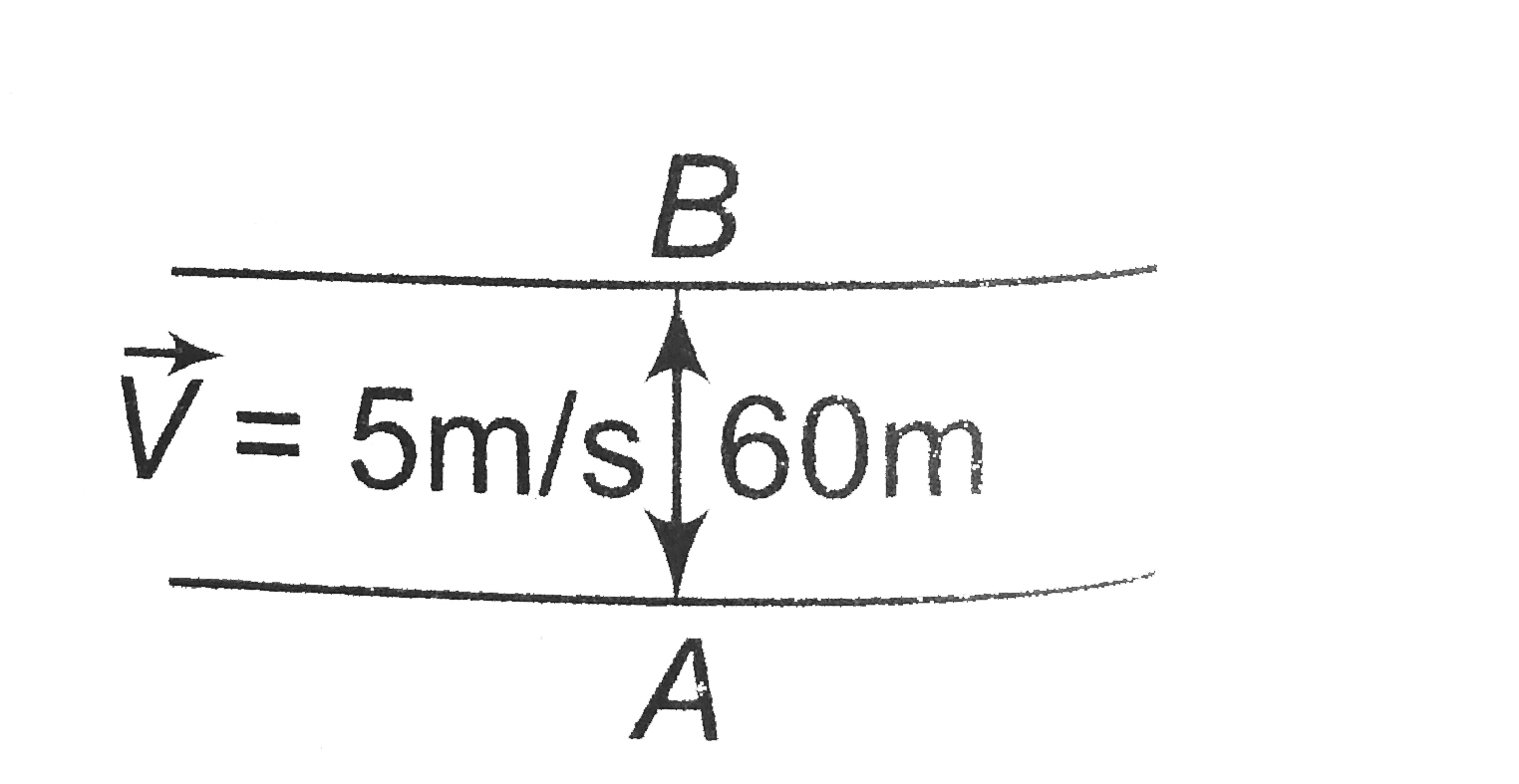
View SolutionA man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5 sec. His velocity in still water should be

View SolutionA man can swim in still water at a speed of 6 kmph and he has to cross the river and reach just opposite point on the other bank. If the river is flowing at a speed of 3 kmph, he has to swim in the direction
View SolutionA man wishes to row across a river flowing to the right with speed of 2m/s. If they velocity that the boat can have VB=4m/s , how should the man row so as to reach across in .
(a) shortest path (b) shortest time .
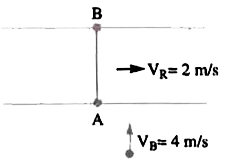
View SolutionA ,man wishing to cross a river flowing with velocity u jumps at an angle θ with the river flow.
(a) Find the net velocity of the man with respect to ground if he can swim with speed v in still water.
(b) In what direction does the boat actually move ?
( c) Find how far from the point directly opposite to the starting point does the boat reach the opposite bank, if the width of the river is d.
View SolutionA swimmer can swim in still water with a speed of 2.5 m/s. What is the shortest time taken by him to swim across the river?

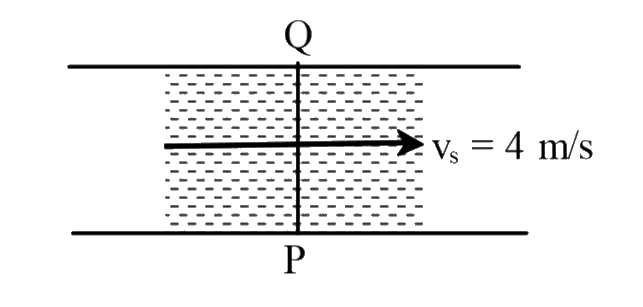
View SolutionA boat man could row his boat with a speed 10 m/sec. He wants to take his boat from P to a point Q just opposite on the other bank of the river flowing at a speed 4 m/sec. He should row his boat–
View SolutionA man can swin with speed 6 km/h in still water. If he tries of swim across a river flowing with speed 5km/h, how fast does a leaf floating on water appears to go , to the man ?
View Solution
