A mass M is attached to a horizontal spring of force constant k fixed one side to a rigid support as shown in figure. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass M is in equilibrium position, another mass m is gently placed on it. When will be the new amplitude of ocillation?
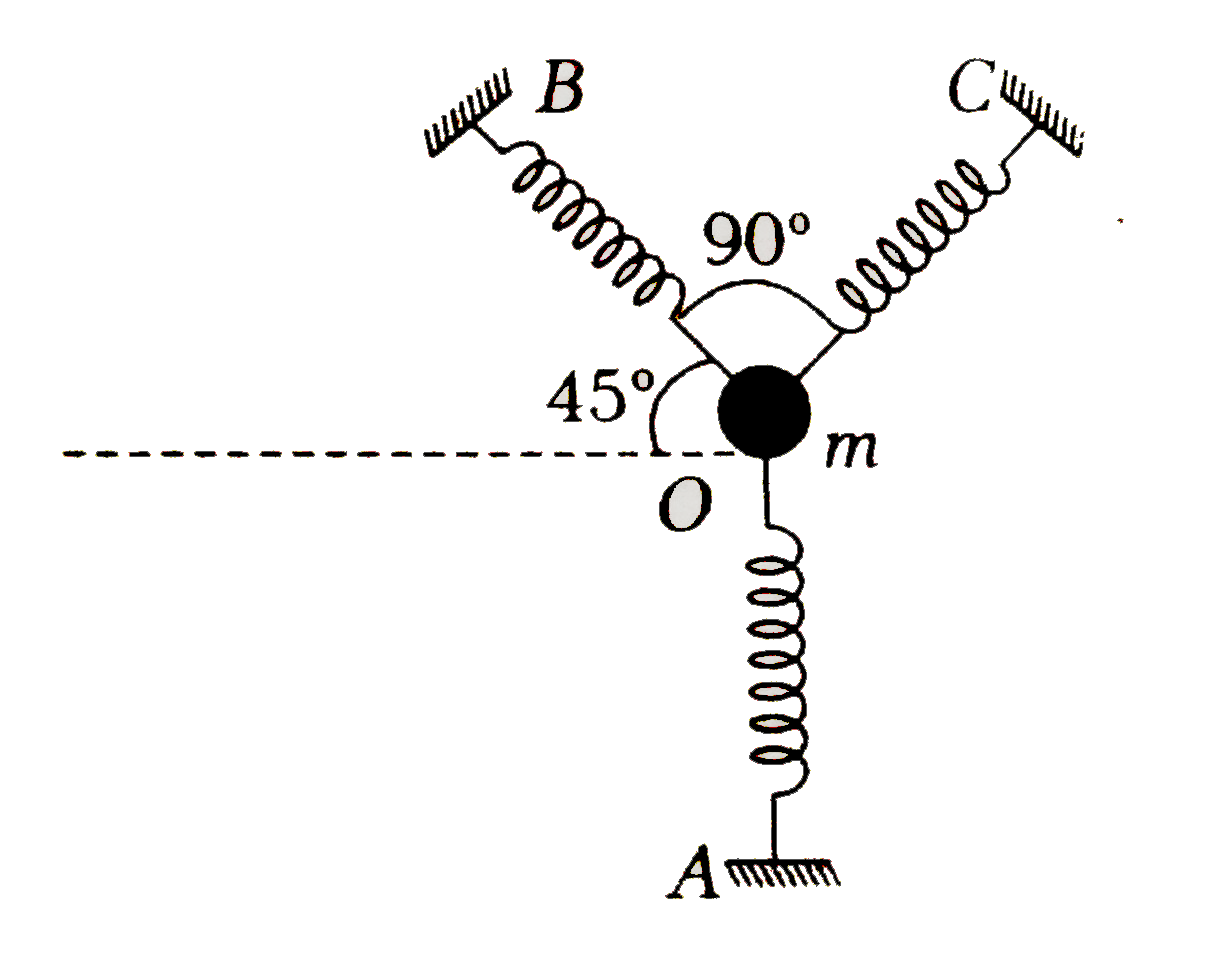

A√MM−m
A√M−mM
A√MM+m
A√M+mM
The correct Answer is:C
T=2π√Mk
When the mass m is placed on mass M, the system of mass attached to the spring is (M+m). New time period of oscillation,
T.=2π√M+mk
Let v be the velocity of the mass M while passing through the mean position and v. be the velocity of the mass (M+m) while passing through the mean position. Then
According to law of conservation of linear momentum
Mv=(M+m)v.
At mean position, v=Aωandv.=A.ω.
∴MAω=(M+m)A.ω.
or A.=(MM+m)ωω.A=MM+m×T.T×A
=(MM+m)×√M+mM×A=A√MM+m
Topper's Solved these Questions
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - CHECK YOUR NEET VITALS
25 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs
43 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs
43 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - MTG GUIDECHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - AIPMT / NEET MCQ
14 Videos
Similar Questions
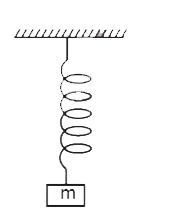
A mass m is attached to the free end of a massless spring of spring constant k with its other end fixed to a rigid support as shown in figure. Find out the time period of the mass, if it is displaced slightly by an amount x downward.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution
Knowledge Check
In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be :
 AA√M−mMBA√MM+mCA√M+mMDA√MM−m
AA√M−mMBA√MM+mCA√M+mMDA√MM−mA particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkA mass m, connected to a horizontal spring performs SHM with amplitude A. While mass m, is passing through mean position, another mass m, is placed on it so that both the masses move together with amplitude A,. The ratio of
A[m1m1+m2]12B[m1+m2m1]12C[m2m1+m2]12D[m1+m2m2]12
A block of mass 'm' is attached to the light spring of force constant K and released when it is in its natural length. Find amplitude of subsequent oscillations.
View SolutionA mass m is suspended from a spring of force constant k and just touches another idential spring fixed to the floras shown in the figure. The time period of small oscillation is
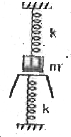
View SolutionWhen a mass M is attached to the spring of force constant k , then the spring stretches by . If the mass oscillates with amplitude l , what will be maximum potential energy stored in the spring
View SolutionThe mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is
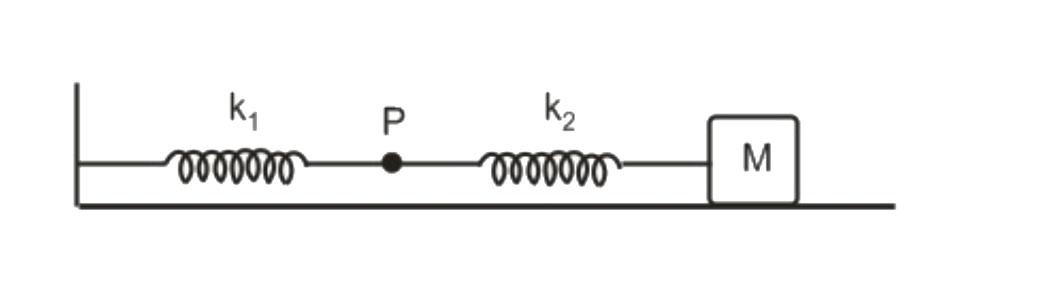
View SolutionThree springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
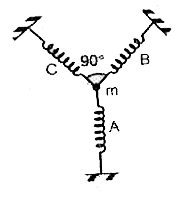
View Solution
