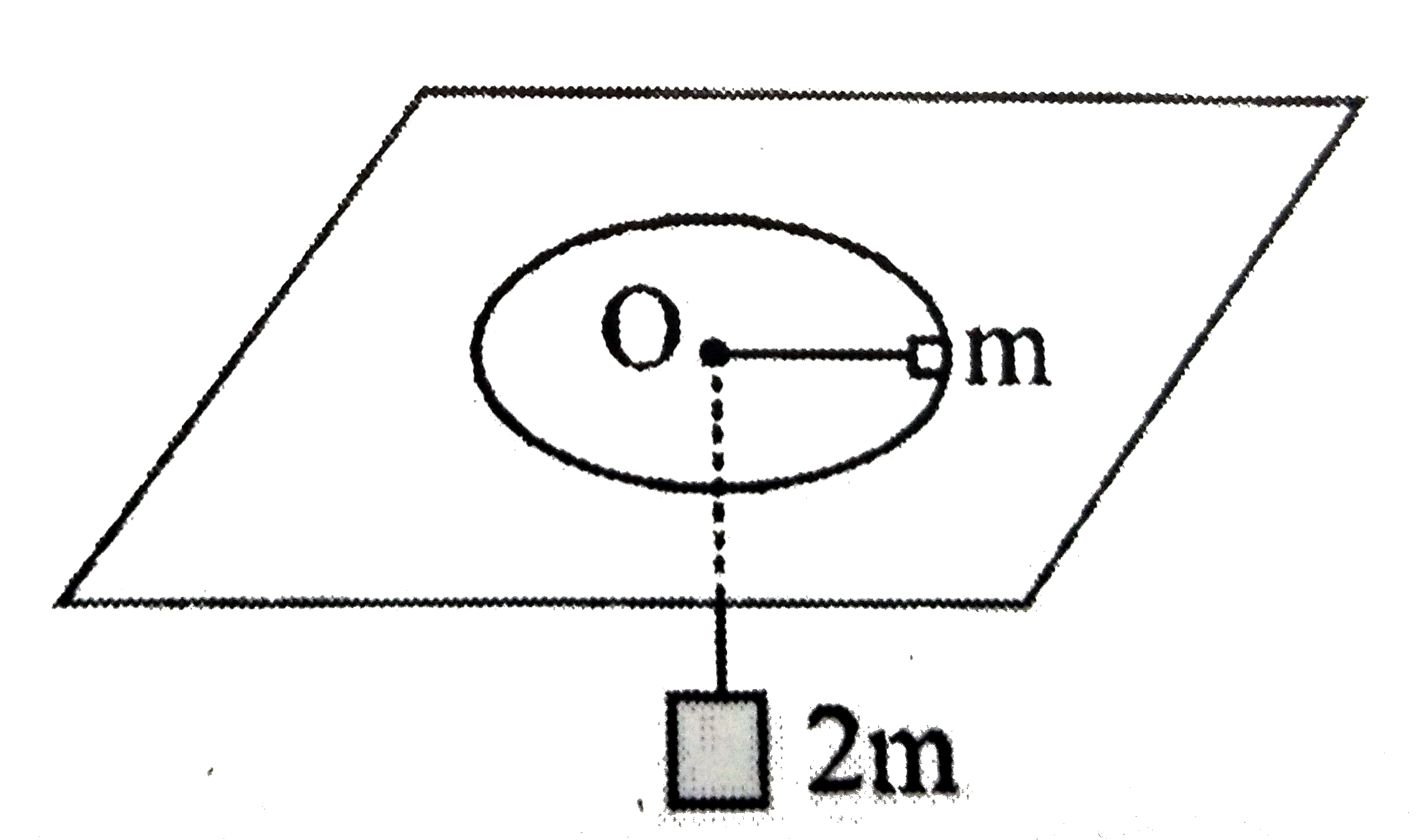
A mass m rotating freely in a horizontal circle of a radius 1m on a frictionless smooth table support a stationary mass 2m, attached to the other end of the string passing through smooth hole O in table, hanging vertically. Find the angular velocity of rotation.
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:√2grad/s
Step by step video & image solution for A mass m rotating freely in a horizontal circle of a radius 1m on a frictionless smooth table support a stationary mass 2m, attached to the other end of the string passing through smooth hole O in table, hanging vertically. Find the angular velocity of rotation. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(S-2)
6 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(O-1)
22 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (S-1)
10 Videos
- BASIC MATHSBOOK - ALLEN CHAPTER - BASIC MATHSEXERCISE - Question
1 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
Similar Questions
A stone is launched upward at 45∘ with speed v0. A bee follow the trajectory of the stone at a constant speed equal to the initial speed of the stone.
(a) Find the radius of curvature at the top point of the trajectory.
(b) What is the acceleration of the bee at the top point of the trajectory? For the stone, neglect the air resistance.
View SolutionThe area of the parallelogram represented by the vectors →A=2ˆi+3ˆj and →B=ˆi+4ˆj is
View SolutionA stone tied at the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 25 revolutions in 14 s, what is the magnitude of acceleration of the stone ?
View SolutionFind dydx for the following :
(i) y=x7/2 (ii) y=x−3
(iii)y=x (iv) y=x5+x3+4x1/2+7
(v) y=5x4+6x3/2+9x (vi) y=ax2+bx+C
(Vii)y=3x^(5)-3x-1/x
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionA thread is passing through a hole at the centre of frictionless table. At the upper end a block of mass 0.5 kg is tied and a block of mass 8.0 kg is tied at the lower end which is freely hanging. The smaller mass is rotate, on the table with a constant angular velocity about the axis passing through the hole so as to balance the heavier mass. If the mass of the hanging block is changed from 8.0 kg to 1.0 kg , what is the fractional change in the radius and the angular velocity of the smaller mass so that it balances the hanging mass again?
View SolutionOne end of a string is attached to a 6kg mass on a smooth horizontal table. The string passes over the edge of the table and to its other end is attached a light smooth pulley.Over this pulley passes another string to the ends of which are attached masses of 4kg and 2kg respectively. Show that the 6kg mass moves with an acceleration of 8g/17.
View SolutionA mass m rotating freely in a horizontal circle of a radius 1m on a frictionless smooth table support a stationary mass 2m, attached to the other end of the string passing through smooth hole O in table, hanging vertically. Find the angular velocity of rotation.

View SolutionA bock of mass M is on a horizontal table and is connected to an inextensible string. The string passes over a frictionless pulley fitted at one edge of the table. At the other end, another block of mass m hangs vertically. Coefficient fo friction between the table and the block of mass is mu . Find the acceleration of the system. Also find the tension in the string.
View SolutionA string passes through a hole at the centre of a horizontal table. The upper end of the string is tied to a mass m kept on the table, and at the lower end, a body of mass M is kept hanging. If the table rotates at an angular velocity omega , the mass M remains at rest. Show that, omega = sqrt((M)/(m)cdot(g)/(r)) . [ r is the radius of the circular path along which the mass m is rotating ]
View SolutionA rod of mass 12 m and length l lying on a smooth horizontal plane can rotate freely about a stationary, vertical axis passing through the rod's end. A particle of mass m moving along the plane with speed v_(0) hits the rod's end perpendicularly and gets stuck there. Find the angular velocity of the system.
View SolutionThere is a small hole in a table. A string of length lm passes through it. Two bodies of masses 70g and 100 g are attached at its ends. The lOOg mass hangs freely at a depth of 60 cm from the table. If this mass is to be in equilibrium, the other mass should rotate in a circle with a frequency equal to
View SolutionThere is a small hole in a table. A string of length 1m passes through it. Two bodies of masses 70g and 100g are attached at its ends. The 100g mass hangs freely at a depth of 60 cm from the table. If this mass is to be in equilibrium, the other mass should rotate in a circle with a frequency equal to
View SolutionThere is a small hole in a table. A string of length 1m passes through it. Two bodies of masses 70g and 100g are attached at its ends. The 100g mass hangs freely at a depth of 60 cm from the table. If this mass is to be in equilibrium, the other mass should rotate in a circle with a frequency equal to
View SolutionThere is a small hole in a table. A string of length 1m passes through it. Two bodies of masses 70g and 100g are attached at its ends. The 100g mass hangs freely at a depth of 60 cm from the table. If this mass is to be in equilibrium, the other mass should rotate in a circle with a frequency equal to
View SolutionThere is a small hole in a table. A string of length 1m passes through it. Two bodies of masses 70g and 100g are attached at its ends. The 100g mass hangs freely at a depth of 60 cm from the table. If this mass is to be in equilibrium, the other mass should rotate in a circle with a frequency equal to
View Solution
