A mass m1 is connected by a weghtless cable of water, whose mass is m0 at t=0. If the container efects water in downward directiona t a constant rate bkg/s. with a velocity v0 relative to the container, determine the acceleration of m1 as a function of time.
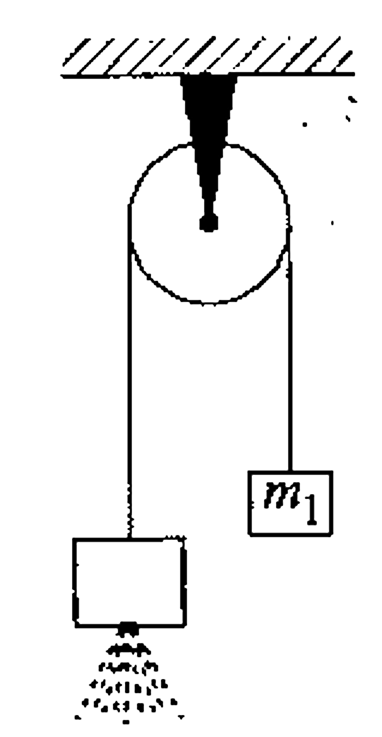
Step by step video & image solution for A mass m_(1) is connected by a weghtless cable of water, whose mass is m_(0) at t=0. If the container efects water in downward directiona t a constant rate bkg/s. with a velocity v_(0) relative to the container, determine the acceleration of m_(1) as a function of time. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Discussio Q
28 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Conceptual MCQ s single option correct
30 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
Similar Questions
An insulated container containing monoatomic gas of molar mass m is moving with a velocity V0. If the container is suddenly stopped , find the change in temperature .
View SolutionA ball of mass M/2 filled with a gas ( whose mass is M/2) is kept on a frictionless table . A bullet of mass m=M/4 and velocity v0ˆi penetrates the ball , and rests inside at t=0. Assume that the amount of gas emitted during the collision can be neglected. The compressed gas is emitted at a contant velocity v0/2 relative to the ball and at an even rate k ( k is a positive constant ) .
(a) What is the velocity of the ball after the collision with the bullet ?
(b) Find the velocity of the ball v(t) as a function of time. Assume that the emission of gas starts at t=0. What is the final velocity of the ball ?

View Solution
Knowledge Check
A block of mass M and cylindrical tank which contains water having small hole at bottom, which is closed initially (total mass of cylinder + water is also M), are attached at two ends of an ideal string which passes over an ideal pulley as shown. At t=0 hole is opened such that water starts coming out of the hole with a constant rate μkg/s and constant velocity Ve relative to the cyliender. aSccleration of the block at any time t will be : (Given that string always remains taut.)
 Aμ(Ve+gt)(2M−μt)BμVe(2M−μt)Cμgt(2M−μt)D2μVe(2M−μt)
Aμ(Ve+gt)(2M−μt)BμVe(2M−μt)Cμgt(2M−μt)D2μVe(2M−μt)An insulated container containing n moles of monoatomic gas of molar mass m is moving with a velocity v0. If the container is suddenly stopped, find the change in temperature.
Amnv203RBmv203nRCmnv20RDmv202RA body of mass m, accelerates uniformly from rest to V1 in time t1. The instantaneous power delivered to the body as a function of time t is.
Amv1t2t1Bmv21tt21Cmv1tt1Dmv21tt1
Two masses m1 and m2 connected by a light spring of natural length l0 is compressed completely and tied by a string. This system while moving with a velocity v0 along +vex-axis pass through the origin at t=0. At this position the string snaps. Postion of mass m1 at time t is given by the equation. x1(t)=v0t−A(1−cosωt) calculate :
(a) Position of the particle m2 as a function of time.
(b) l0 in terms of A.
View SolutionTwo masses m1 and m2 concute a high spring of natural length l0 is compressed completely and tied by a string. This system while conving with a velocity v0 along +ve x-axis pass thorugh the origin at t=0, at this position the string sanps, Position of mass m1 at time t is given by the equation x1t=v0(A/1−cosωt). Calculate (i) position of the particle m2 as a funcation of time, (ii) l0 in terms of A.
View SolutionA body of mass m, accelerates uniformly from rest to v1 in time t1. Find the instantaneous power delivered to the body as a function of time t.
View SolutionA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionThe rate of mass of the gas emitted from the rear of a rocket is initially 0.1kg/s. If the speed of the gas relative to the rocket is 50m/s and the mass of the rocket is 2kg , then the acceleration of the rocket in m/s2 is
View Solution
