A mass m1 is connected by a weghtless cable of water, whose mass is m0 at t=0. If the container release water in downward direction at constant rate b kg/s. with a velocity v0 relative to the container, determine the acceleration of m1 as a function of time.
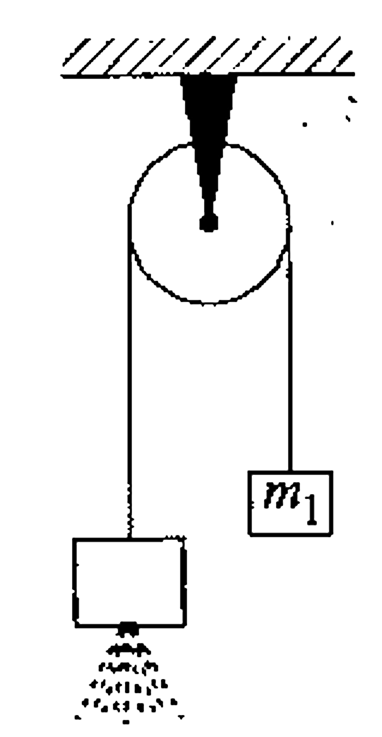
The correct Answer is:(m1−m0+kt)g+kv0(m1+m0−kt)
Writing equations:
m1g−T=m1a ...(i)
T−mg=ma ....(ii)
Adding equations (i) and (ii)
g(m1−m)=(m1+m)a ....(iii)
As −dmdt=k
−m∫m0dm=t∫0kdt
m0−m=kt+C
m0−kt=m
By putting value of m in equation (iii) we get acceleration
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Objective Questions
134 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - More than one choice is correct
15 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Problem
33 Videos
- BASIC MATHEMATICSBOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
Similar Questions
A mass m1 is connected by a weghtless cable of water, whose mass is m0 at t=0. If the container efects water in downward directiona t a constant rate bkg/s. with a velocity v0 relative to the container, determine the acceleration of m1 as a function of time.

View SolutionAn insulated container containing monoatomic gas of molar mass m is moving with a velocity V0. If the container is suddenly stopped , find the change in temperature .
View Solution
Knowledge Check
A block of mass M and cylindrical tank which contains water having small hole at bottom, which is closed initially (total mass of cylinder + water is also M), are attached at two ends of an ideal string which passes over an ideal pulley as shown. At t=0 hole is opened such that water starts coming out of the hole with a constant rate μkg/s and constant velocity Ve relative to the cyliender. aSccleration of the block at any time t will be : (Given that string always remains taut.)
 Aμ(Ve+gt)(2M−μt)BμVe(2M−μt)Cμgt(2M−μt)D2μVe(2M−μt)
Aμ(Ve+gt)(2M−μt)BμVe(2M−μt)Cμgt(2M−μt)D2μVe(2M−μt)An insulated container containing n moles of monoatomic gas of molar mass m is moving with a velocity v0. If the container is suddenly stopped, find the change in temperature.
Amnv203RBmv203nRCmnv20RDmv202RA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
AconstantBabt2Cabt2mDa2bt2m
A ball of mass M/2 filled with a gas ( whose mass is M/2) is kept on a frictionless table . A bullet of mass m=M/4 and velocity v0ˆi penetrates the ball , and rests inside at t=0. Assume that the amount of gas emitted during the collision can be neglected. The compressed gas is emitted at a contant velocity v0/2 relative to the ball and at an even rate k ( k is a positive constant ) .
(a) What is the velocity of the ball after the collision with the bullet ?
(b) Find the velocity of the ball v(t) as a function of time. Assume that the emission of gas starts at t=0. What is the final velocity of the ball ?

View SolutionTwo masses m1 and m2 connected by a light spring of natural length l0 is compressed completely and tied by a string. This system while moving with a velocity v0 along +vex-axis pass through the origin at t=0. At this position the string snaps. Postion of mass m1 at time t is given by the equation. x1(t)=v0t−A(1−cosωt) calculate :
(a) Position of the particle m2 as a function of time.
(b) l0 in terms of A.
View SolutionFigure 5-50 shows Atwood's machine, in which two containers are connected by a cord (of negligible mass) passing over a frictionless pulley (also of negligible mass). At time t = 0, container 1 has mass 1.30 kg and container 2 has mass 2.80 kg, but container 1 is losing mass (through a leak) at the constant rate of 0.200 kg/s. At what rate is the acceleration magnitude of the containers changing at (a) t = 0 and (b) t = 3.00 s? (c) When does the acceleration reach its maximum value ?
View SolutionA body of mass m, accelerates uniformly from rest to V1 in time t1. The instantaneous power delivered to the body as a function of time t is.
View SolutionThe rate of mass of the gas emitted from the rear of a rocket is initially 0.1kg/s. If the speed of the gas relative to the rocket is 50m/s and the mass of the rocket is 2kg , then the acceleration of the rocket in m/s2 is
View Solution
