A mass of 2kg is attached to the spring of spring constant . The block is pulled to a distance of 5 cm from its equilibrium position at on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
To find the expression for the displacement of a mass attached to a spring undergoing simple harmonic motion (SHM), we can follow these steps:
Step 1: Identify the parameters
Given:
- Mass m=2kg
- Spring constant k=50N/m
- Displacement from equilibrium (amplitude) A=5cm=0.05m
Step 2: Calculate the angular frequency ω
The angular frequency ω for a mass-spring system is given by the formula:
ω=√km
Substituting the values:
ω=√502=√25=5rad/s
Step 3: Determine the initial phase ϕ
At t=0, the mass is pulled to its maximum displacement (amplitude), which means:
x(0)=A=0.05m
The general equation for displacement in SHM is:
x(t)=Asin(ωt+ϕ)
At t=0:
x(0)=Asin(ϕ)=0.05
Since the mass starts from rest at maximum displacement, we can use the cosine function instead:
x(t)=Acos(ωt+ϕ)
At t=0:
0.05=Acos(ϕ)
Since A=0.05:
0.05=0.05cos(ϕ)⟹cos(ϕ)=1⟹ϕ=0
Step 4: Write the displacement equation
Now substituting A, ω, and ϕ into the displacement equation:
x(t)=0.05cos(5t+0)
Thus, the expression for displacement becomes:
x(t)=0.05cos(5t)
Final Expression
The final expression for the displacement of the mass at any time t is:
x(t)=0.05cos(5t)m
---
Given:
- Mass m=2kg
- Spring constant k=50N/m
- Displacement from equilibrium (amplitude) A=5cm=0.05m
The angular frequency ω for a mass-spring system is given by the formula:
ω=√km
Substituting the values:
ω=√502=√25=5rad/s
At t=0, the mass is pulled to its maximum displacement (amplitude), which means:
x(0)=A=0.05m
The general equation for displacement in SHM is:
x(t)=Asin(ωt+ϕ)
At t=0:
x(0)=Asin(ϕ)=0.05
Since the mass starts from rest at maximum displacement, we can use the cosine function instead:
x(t)=Acos(ωt+ϕ)
At t=0:
0.05=Acos(ϕ)
Since A=0.05:
0.05=0.05cos(ϕ)⟹cos(ϕ)=1⟹ϕ=0
Now substituting A, ω, and ϕ into the displacement equation:
x(t)=0.05cos(5t+0)
Thus, the expression for displacement becomes:
x(t)=0.05cos(5t)
The final expression for the displacement of the mass at any time t is:
x(t)=0.05cos(5t)m
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Very Short Answer Type Qns14videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - Long answer type questions12videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
A block whose mass is 1 kg is fastened to a spring.The spring has a spring constant 50Nm−1. The block is pulled to a distance x=10cm from its equilibrium position at x=0 on a frictionless surface at t=0. Calculate the kinetic, potential and total energies of the block when it is 5cm away from the mean position.
View SolutionA block whose mass is 2 kg is fastened on a spring whose spring constant is 100 Nm−1 . It is pulled to a distance of 0.1 m from over a frictionless surface and is released at t=0. Calculate the kinetic eneryg of the block when it is 0.05 m away from its mean position.
View Solution
Knowledge Check
- Question 1 - Select One
A block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of 100N/m. the block is pulled to a distance x=10 cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. the kinetic energy and potential energy of the block when it is 5 cm away from the mean position is
A0.0375 J, 0.125 JB0.125 J, 0.375 JC0.125 J, 0.125 JD0.375 J, 0.375 J - Question 2 - Select One
A 5 kg collar is attached to a spring of spring constant 500 N m−1. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. The time period of oscillation is
Aπ5sBπ2sCπsD2πs
A 10 kg metal block is attached to a spring constant 1000Nm−1. A block is displaced from equilibrium position by 10 cm and released. The maximum acceleration of the block is
View SolutionA 2.5 kg collar is attached to a spring of spring constant 250Nm−1 . It slides without friction over a horizontal surface . It is displaced from its equilibrium position by 20 cm and releasd. Calculate the period of osciallation and the maximum speed.
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
 View Solution
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximum speed of the trolley is
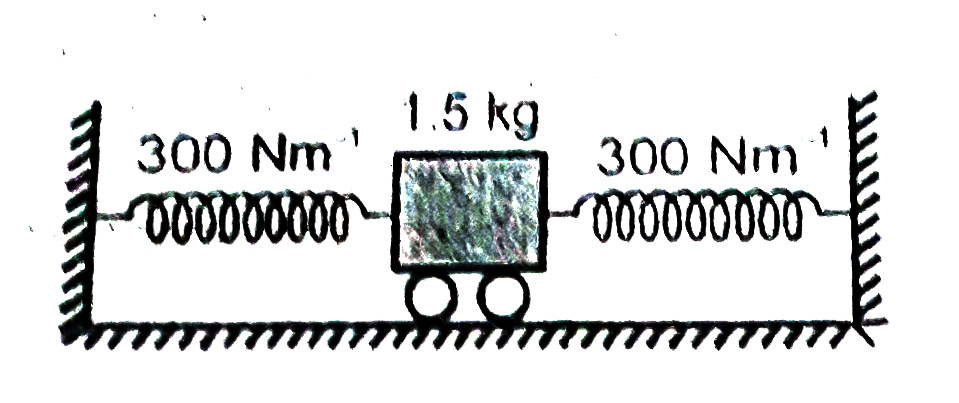 View Solution
View SolutionA block of mass m=0.1kg is connected to a spring of unknown spring constant k. It is compressed to a distance x from its equilibrium position and released from rest. After approaching half the distance (x2) from the equilibrium position, it hits another block and comes to rest momentarily, while the other block moves with velocity 3ms−1. The total initial energy of the spring is :
View Solution

