A mass of 4 kg suspended from a spring of spring constant 800Nm−1 executes simple harmonic oscillations. If the total energy of the oscillator is 4 J, the maximum acceleration (in ms−2) of the mass is
5
15
45
20
The correct Answer is:D
To solve the problem, we need to find the maximum acceleration of a mass executing simple harmonic motion (SHM). Here are the steps to arrive at the solution:
Step 1: Identify the given values
- Mass (m) = 4 kg
- Spring constant (k) = 800 N/m
- Total energy (E) = 4 J
Step 2: Use the formula for total energy in SHM
The total energy (E) of a mass-spring system in simple harmonic motion is given by the formula:
E=12kA2
where A is the amplitude.
Step 3: Rearrange the formula to find the amplitude (A)
From the total energy formula, we can rearrange it to solve for A:
A2=2Ek
Substituting the known values:
A2=2×4J800N/m
A2=8800=0.01
Taking the square root:
A=√0.01=0.1m
Step 4: Calculate the angular frequency (ω)
The angular frequency ω is given by:
ω=√km
Substituting the values:
ω=√800N/m4kg
ω=√200
Step 5: Calculate the maximum acceleration (a_max)
The maximum acceleration amax in SHM can be calculated using the formula:
amax=ω2A
Substituting the values we have:
amax=(200)×(0.1)
amax=20m/s2
Final Answer
Thus, the maximum acceleration of the mass is:
20m/s2
- Mass (m) = 4 kg
- Spring constant (k) = 800 N/m
- Total energy (E) = 4 J
The total energy (E) of a mass-spring system in simple harmonic motion is given by the formula:
E=12kA2
where A is the amplitude.
From the total energy formula, we can rearrange it to solve for A:
A2=2Ek
Substituting the known values:
A2=2×4J800N/m
A2=8800=0.01
Taking the square root:
A=√0.01=0.1m
The angular frequency ω is given by:
ω=√km
Substituting the values:
ω=√800N/m4kg
ω=√200
The maximum acceleration amax in SHM can be calculated using the formula:
amax=ω2A
Substituting the values we have:
amax=(200)×(0.1)
amax=20m/s2
Thus, the maximum acceleration of the mass is:
20m/s2
Topper's Solved these Questions
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - CHECK YOUR NEET VITALS
25 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs
43 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs
43 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - MTG GUIDECHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - AIPMT / NEET MCQ
14 Videos
Similar Questions

The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View SolutionA mass suspended from a spring of spring constant k is made to oscillate with a time period T. Now, the spring is cut into three equal parts and the mass is suspended from one of the parts. What will be the new time period of oscillations?
View Solution
Knowledge Check
A body of mass 20 g connected to a spring of spring constant k, executes simple harmonic motion with a frequency of (5/π) Hz. The value of spring constant is
A4Nm−1B3Nm−1C2Nm−1D5Nm−1A 0.20kg object mass attached to a spring whose spring constant is 500N/m executes simple harmonic motion. If its maximum speed is 5.0m/s, the amplitude of its oscillation is
A0.0020mB0.10mC0.20mD25mA body of mass 1 kg suspended by a light vertical spring of spring constant 100 N/m executes SHM. Its angular frequency and frequency are
A5π rad/s, 100 HzB10 rad/s, π5 HzC10 rad/s, 10π HzD10 rad/s, 5π Hz
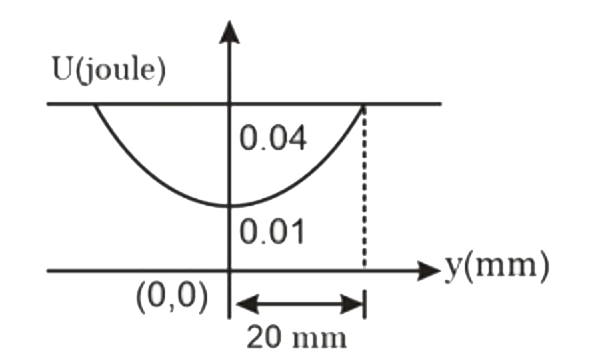
The variation of the potential energy of harmonic oscillator is as shown in the figure. The spring constant is
View SolutionA mass is suspended from a spring have spring constant k is displaced veritcally and relased it oscillates with period T the weight of the mass suspended is (g= gravitatioanal acceleration)
View SolutionA mass is suspended from a spring have spring constant k is displaced veritcally and relased it oscillates with period T the weight of the mass suspended is (g= gravitatioanal acceleration)
View SolutionA particle of mass 3 kg , attached to a spring with force constant 48Nm−1execute simple harmonic motion on a frictionless horizontal surface. The time period of oscillation of the particle, is seconds , is
View SolutionA mass M is suspended from a spring of negiliglible mass the spring is pulled a little and then released so that the mass executes simple harmonic oscillation with a time period T If the mass is increases by m the time period because (54T),The ratio of mM is
View Solution
