A metal ball of radius a is surrounded by a thin concentric metal shell of radius b. The space between these electrodes is filled up with a poorly conducting homogenous medium of resistivity ρ. Find the resistance of the interelectrode gap. Analyse the obtained solution at b→∞.
(a) Taking an element of a spherical shell of radius r and thickness dr.
dA=4πr2
l=dr
dR=ρldA=ρdr4πr2
R=ρ4π∫bar−2dr
=ρ4π∣∣∣r−1−1∣∣∣ba=ρ4π∣∣∣−1r∣∣∣ba
=−ρ4π∣∣∣1r∣∣∣ba=−ρ4π∣∣∣1b−1a∣∣∣=ρ4π(b−a)ab
R=ρ(b−a)4πab
When b→∞
R=−ρ4π(1∞−1a)=ρ4πa
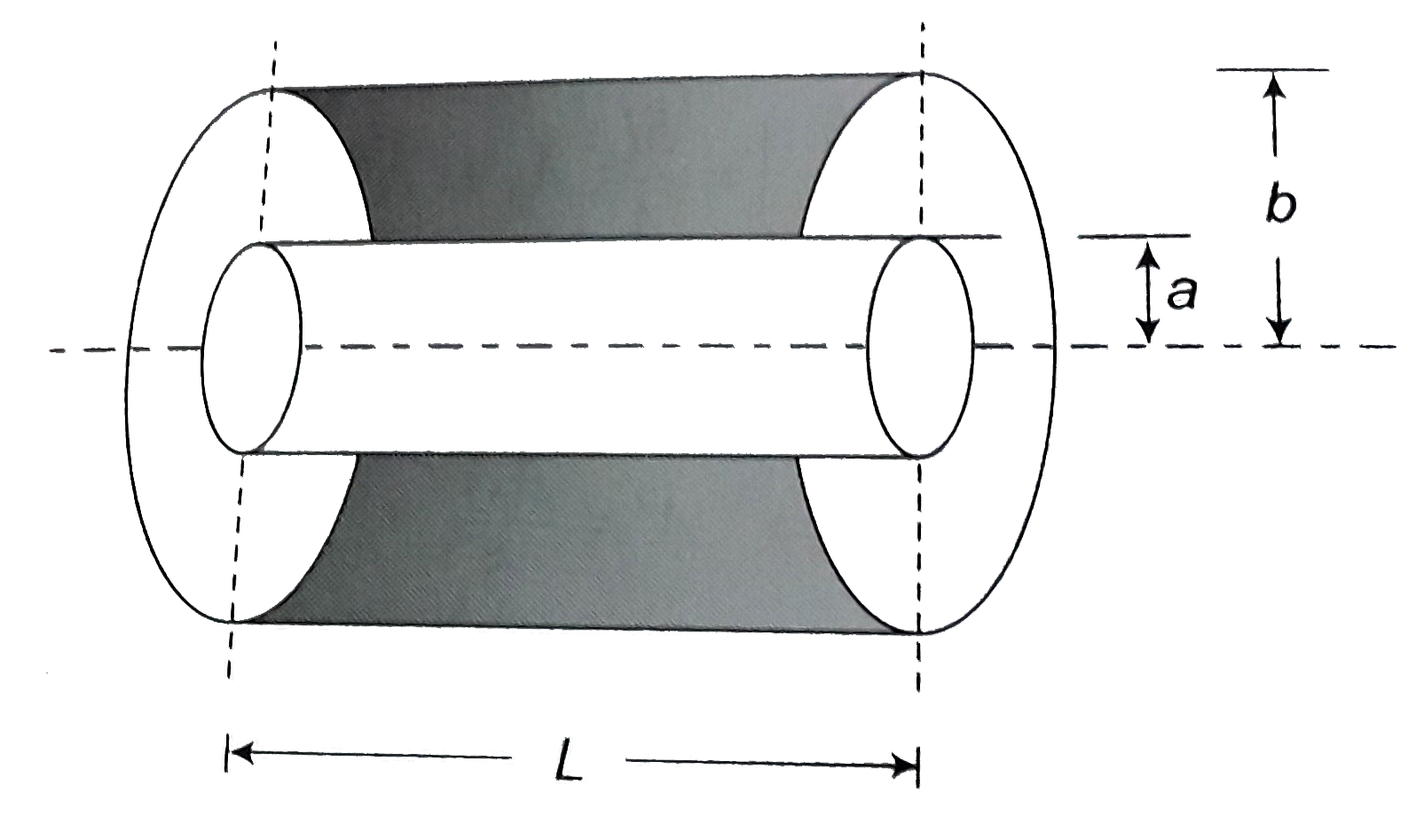
(b) (i) Area of cross-section A=π(b2−a2)
R=ρLA=ρLπ(b2−a2)
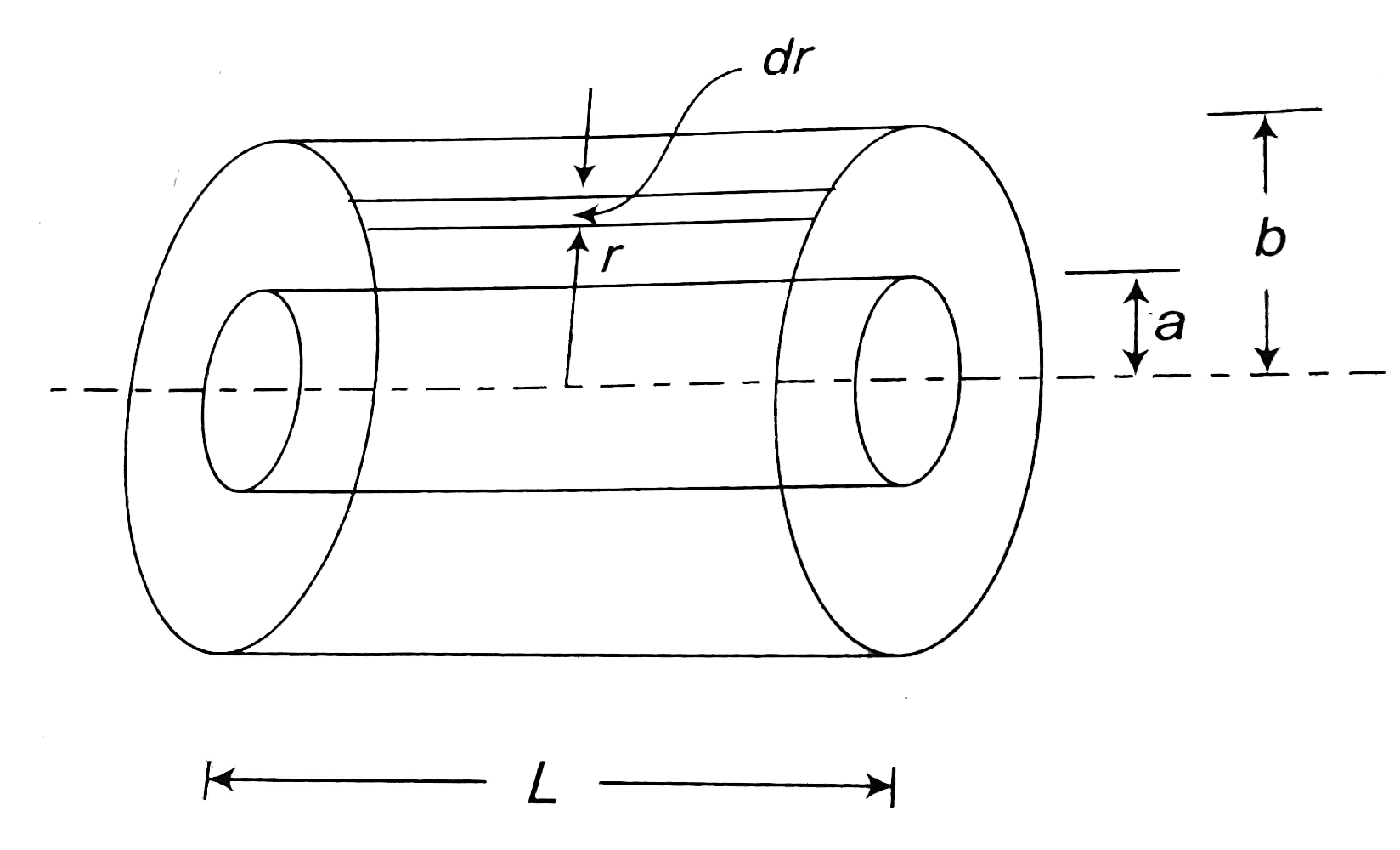
(ii) Taking an element a cylindrical shell of radius r and thickness dr
A=2πrL
dR=ρdr2πrL
R=ρ2πL∫badrr=ρ2πL|loger|ba
=ρ2πL(logeb−logea)=ρloge(b/a)2πL
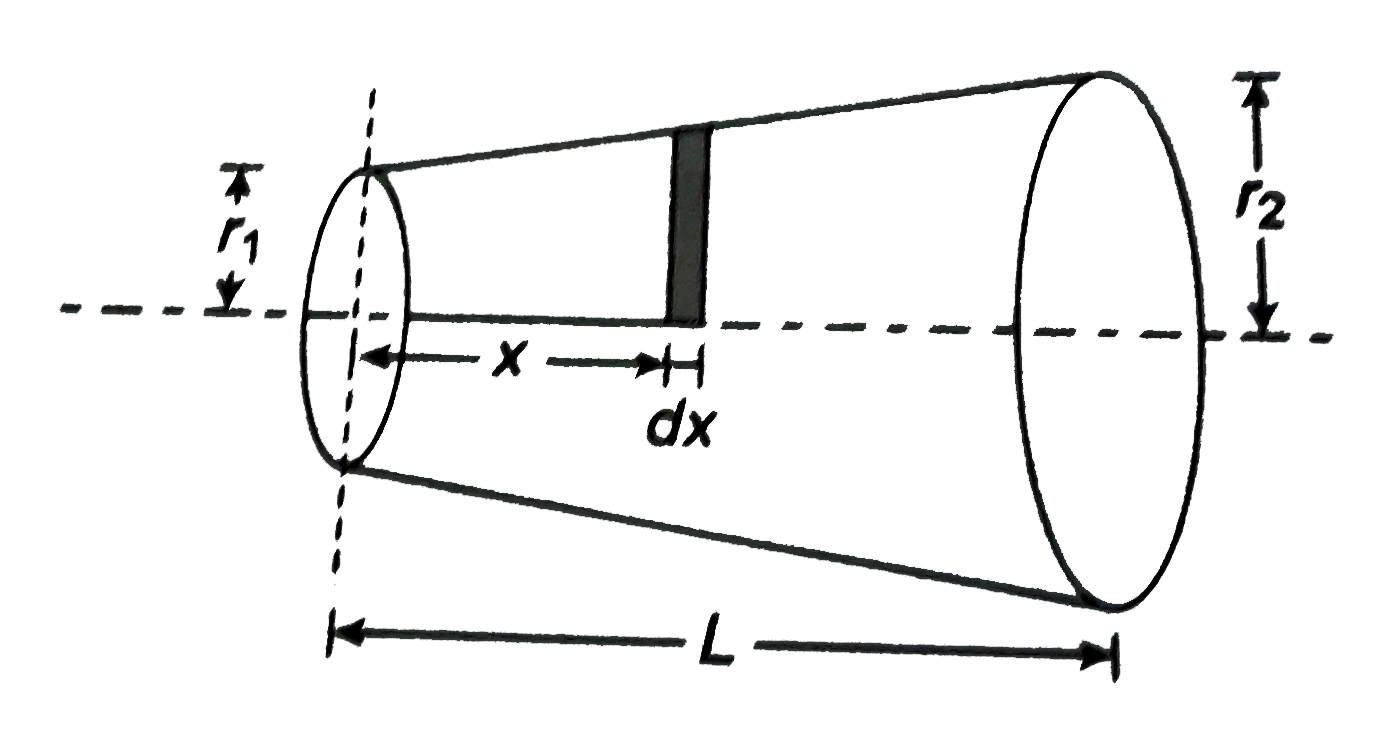
( c) rx=r1+r2−r1Lx
=r1+λx,
where λ=r2−r1L
dR=ρdxπr2x=ρdxπ(r1+λx)2
R=ρπ∫L0dx(r1+λx)2
=ρπ∣∣
∣∣(r1+λx)−1(−1)(λ)∣∣
∣∣L0
=−ρπλ∣∣∣1r1+λx∣∣∣L0
=−ρπλ∣∣∣1r1+λL−1r1∣∣∣
=−ρπλ∣∣∣1r2−1r1∣∣∣=ρπλ(r2−r1)r1r2
=ρLπr1r2
In case of frustum of cone, take area as
A=√A1A2=√πr21.πr22=πr1r2
(d) Taking an element of area A and separation between plates dx.
Conductivity at distance x from the left end.
σx=σ1+σ2−σ1Lx=σ1+λx
where λ=σ2−σ1L
dR=ρxdxA=dxσxA=dx(σ1+λx)A
R=1A∫L0dx(σ1+λx)
=1A|loge(σ1+λx)|L0λ
=1Aλ[loge(σ1+λL)−loge(σ1)]
=1Aλ[loge(σ2)−loge(σ1)]
=1A(σ2−σ1)Lloge(σ2σ1)
=Lloge(σ2/σ1)A(σ2−σ1).

 ,
,
Topper's Solved these Questions
Similar Questions
There are two concentric spheres of radius a and b respectively. If the space between them is filled with medium of resistivity ρ, then the resistance of the intergap between the two spheres will be (Assume b>a)
View SolutionA metal ball of radius a is located at a distance l from an indinite ideally conducting plane. The space around the ball is filled with a homongeous poorly conducting medium with resistivity ρ. In the case of a<<l find :
(a) the current density at the conducting plane as a function of distance r from the ball if the potentail difference between the ball and the plane is equal to V ,
(b) the electric resistance of the medium between the balll and the plane.
View Solution
Knowledge Check
A metallic spherical shell of radius r1 is surrounded by another concentric metallic spherical shell of radius r2. The space between the two shells is filled with a dielectric of dielectric constant K. If a charge Q is given to the inner shell, the charge appearing on the outer surface of the outer shell is
A+QB+Qr21r22C+QKr21r22DQ[1−1K]
Two metal balls of the same radius a are located in a homongenous poorly conducting medium with resistivity ρ. Find the resistance of the medium between the balls provided that the separation between them is mush greater than the radius of the ball.
View SolutionTwo metal balls of the same radius a are located in a homongenous poorly conducting medium with resistivity ρ. Find the resistance of the medium between the balls provided that the separation between them is mush greater than the radius of the ball.
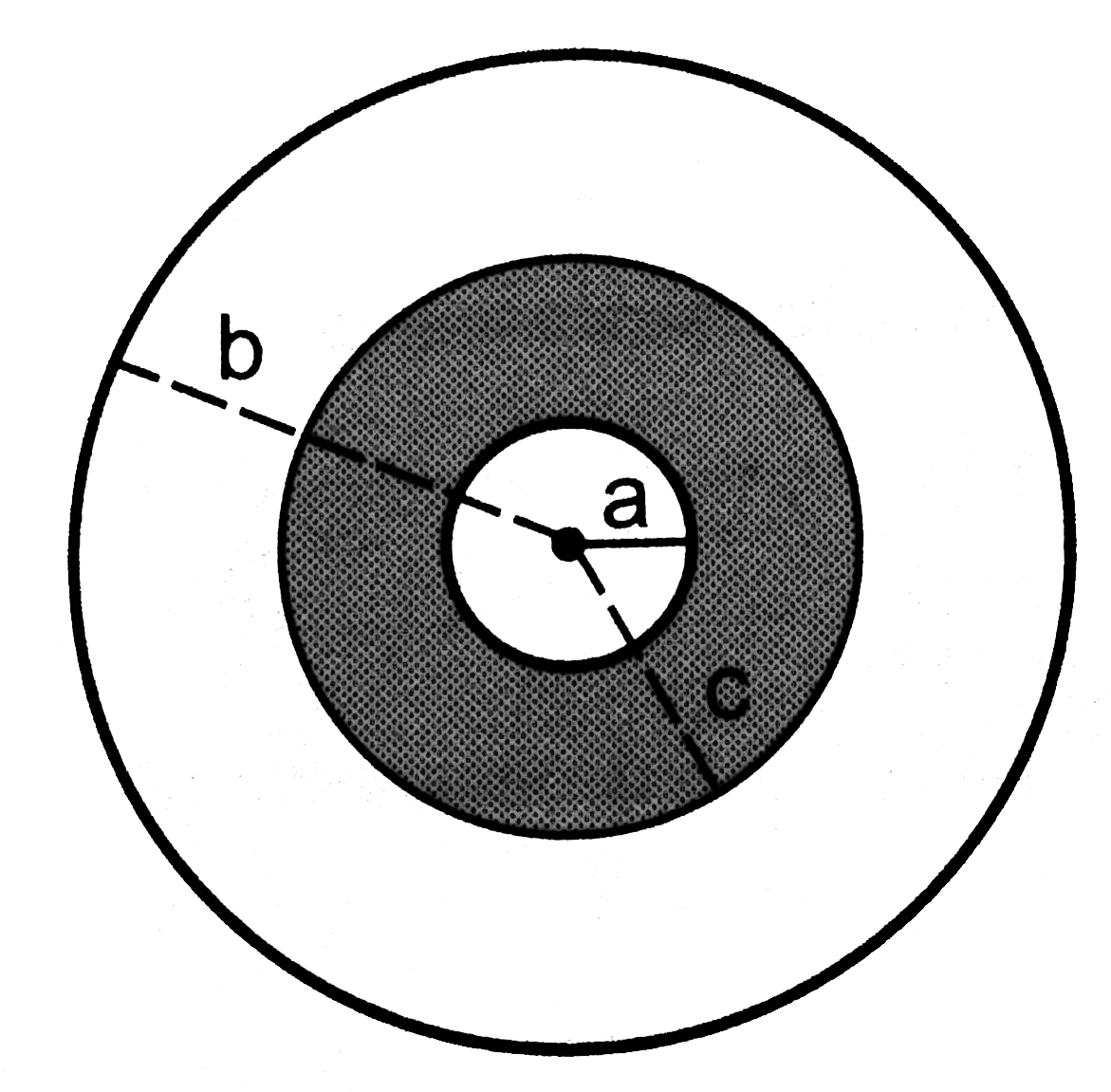
View SolutionA sphercial capacitor is made of two conducting spherical shells of radii a and b.The space between the shells is filled with a dielectric constant Kup to a radius c as shown in figure. Calculate the capacitance .
View SolutionA solid conducting sphere of radius R is surrounded by a concentric metallic shell of inner radius 2R and outer radius 3R. The shell is earthed. The inner sphere is connected to a switch S by a thin conducting wire through a small hole in the shell. By closing the switch S, the inner sphere is connected to a distant conducting sphere of radius R having charge Q. Find the charge that flows to earth through wire AB.
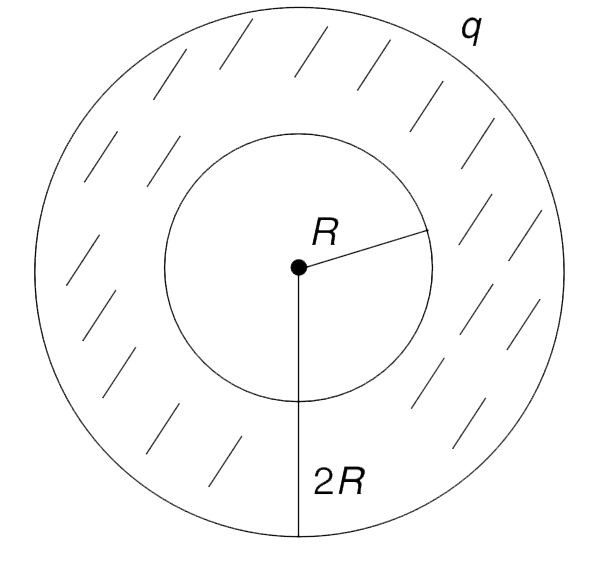
View SolutionA solid conducting sphere of radius R is surrounded by a concentric metallic shell of inner radius 2R and outer radius 3R. The shell is earthed. The inner sphere is connected to a switch S by a thin conducting wire through a small hole in the shell. By closing the switch S, the inner sphere is connected to a distant conducting sphere of radius R having charge Q. Find the charge that flows to earth through wire AB.

View SolutionA uniform metal sphere of radius R and mass m is surrounded by a thin uniform spherical shell of same mass and radius 4R. The centre of the shell C falls on the surface of the inner sphere. Find the gravitational fields at points A and B.

View SolutionA hollow metallic sphere of radius 20cm surrounds a concentric metallic sphere of radius 5cm. The space between the two sphere is filled with a nonmetallic material. The inner and outer sphere are maintained at 50∘C and 10∘C respectively and it is found that 100J of heat passes from the inner sphere to the outer sphere per second. Find the thermal conductivity of the material between the sphere.
View Solution
