There are two concentric spheres of radius a and b respectively. If the space between them is filled with medium of resistivity ρ, then the resistance of the intergap between the two spheres will be (Assume b>a)
To find the resistance of the intergap between two concentric spheres of radius a and b (where b>a) filled with a medium of resistivity ρ, we can follow these steps:
Step 1: Understand the Geometry
We have two concentric spheres with radii a and b. The space between them is filled with a medium of resistivity ρ. We need to calculate the resistance of the spherical shell formed between these two spheres.
Step 2: Consider a Thin Spherical Shell
Consider a thin spherical shell at a distance x from the center, with thickness dx. The radius of this shell is x.
Step 3: Calculate the Resistance of the Thin Shell
The resistance dR of this thin shell can be calculated using the formula:
dR=ρdxA
where A is the surface area of the shell. For a sphere, the surface area A is given by:
A=4πx2
Thus, the expression for dR becomes:
dR=ρdx4πx2
Step 4: Integrate to Find Total Resistance
To find the total resistance R between the spheres, we need to integrate dR from x=a to x=b:
R=∫badR=∫baρdx4πx2
Step 5: Perform the Integration
The integral can be computed as follows:
R=ρ4π∫ba1x2dx
The integral of 1x2 is:
∫1x2dx=−1x
Thus, we have:
R=ρ4π(−1x)ba=ρ4π(−1b+1a)
This simplifies to:
R=ρ4π(1a−1b)
Final Result
The resistance of the intergap between the two spheres is given by:
R=ρ4π(1a−1b)
---
We have two concentric spheres with radii a and b. The space between them is filled with a medium of resistivity ρ. We need to calculate the resistance of the spherical shell formed between these two spheres.
Consider a thin spherical shell at a distance x from the center, with thickness dx. The radius of this shell is x.
The resistance dR of this thin shell can be calculated using the formula:
dR=ρdxA
where A is the surface area of the shell. For a sphere, the surface area A is given by:
A=4πx2
Thus, the expression for dR becomes:
dR=ρdx4πx2
To find the total resistance R between the spheres, we need to integrate dR from x=a to x=b:
R=∫badR=∫baρdx4πx2
The integral can be computed as follows:
R=ρ4π∫ba1x2dx
The integral of 1x2 is:
∫1x2dx=−1x
Thus, we have:
R=ρ4π(−1x)ba=ρ4π(−1b+1a)
This simplifies to:
R=ρ4π(1a−1b)
The resistance of the intergap between the two spheres is given by:
R=ρ4π(1a−1b)
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - C.U.Q
105 Videos
- CURRENT ELECTRICITYBOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - Level 1 C.W
64 Videos
- COMMUNICATION SYSTEMBOOK - NARAYNACHAPTER - COMMUNICATION SYSTEMEXERCISE - Level-II(H.W)
25 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NARAYNACHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ASSERTION AND REASON
15 Videos
Similar Questions
A metal ball of radius a is surrounded by a thin concentric metal shell of radius b. The space between these electrodes is filled up with a poorly conducting homogenous medium of resistivity ρ. Find the resistance of the interelectrode gap. Analyse the obtained solution at b→∞.
View SolutionTwo spheres A and B of radius a and b respectively are at the same potential. The ratio of the surface charge density of A to B is
View Solution
Knowledge Check
Space between tow concentric spheres of radii r1andr2 such that r1<r2 is filled with a material of resistivity ρ. Find the resistance between inner and outer surface of the material
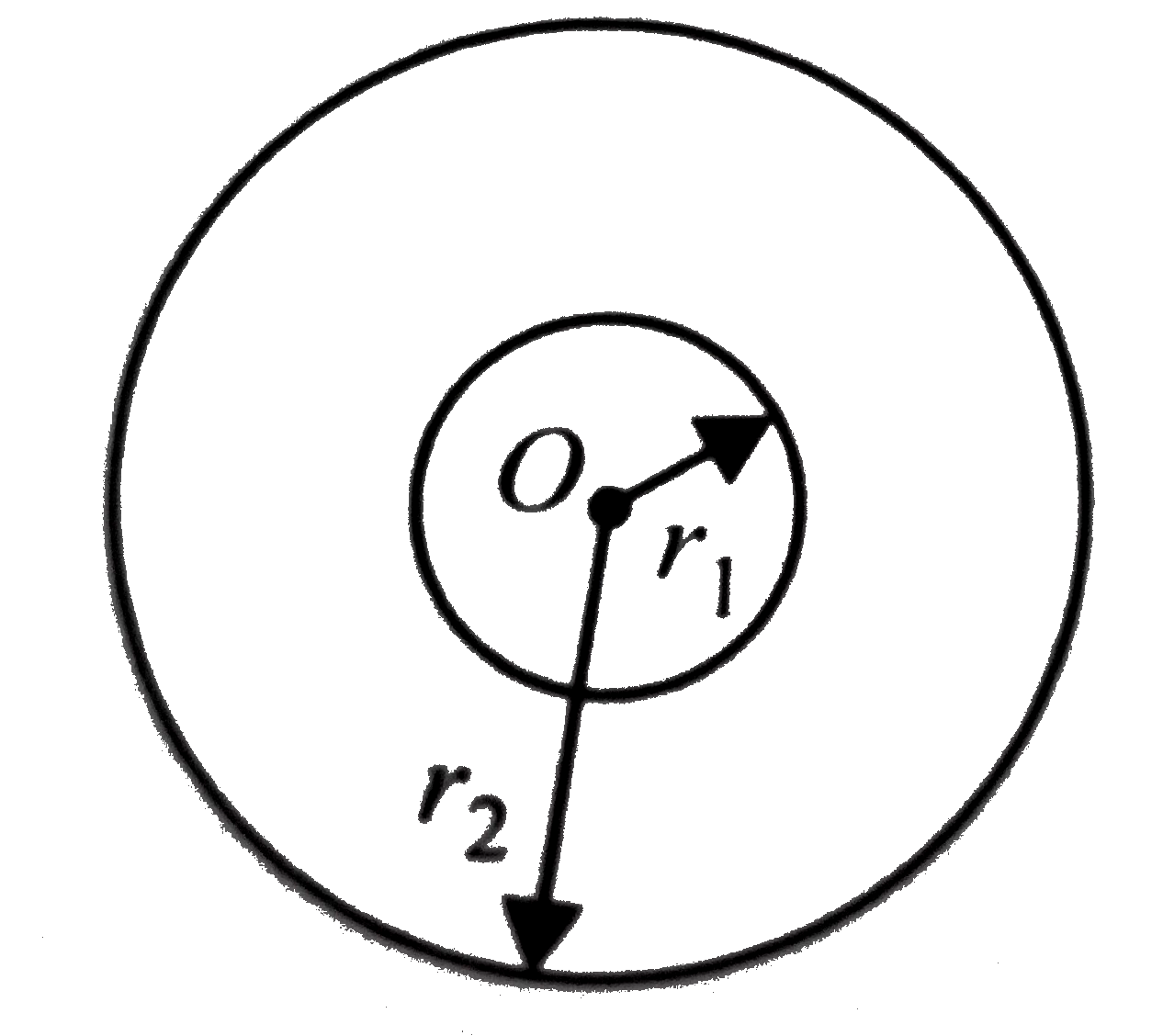 Ar1r2p2Br2−r1r1r2p4πCr1r2r2−r1p4πDnone of these.
Ar1r2p2Br2−r1r1r2p4πCr1r2r2−r1p4πDnone of these.A spherical condenser has inner and outer spheres of radii a and b respectively the space between the two is filled with air the difference between the capacities of two condensers formed when outer sphere is earthed and when inner sphere is earthed will be
AzeroB4πε0aC4πε0bD4πε0a(bb−a)A spherical condenser has inner and outer spheres of radii a and b respectively the space between the two is filled with air the difference between the capacities of two condensers formed when outer sphere is earthed and when inner sphere is earthed will be
AzeroB4πε0aC4πε0bD4πε0a(bb−a)
The masses of two spheres are 10 kg and 20 kg respectively. If the distance between their centres is 100m, find the magnitude of the gravitational force between them.
View SolutionA spherical condenser has innder and outer spheres of radii a and b respectively. The space between the two is filled with air. The difference between the capacities of two condensers formed when outer sphere is earthed and when inner sphere is earthed will be
View SolutionTwo concentric conducting spheres of radii R and 2R are crrying charges Q and −2Q, respectively. If the charge on inner sphere is doubled, the potetial differece between the two spheres will
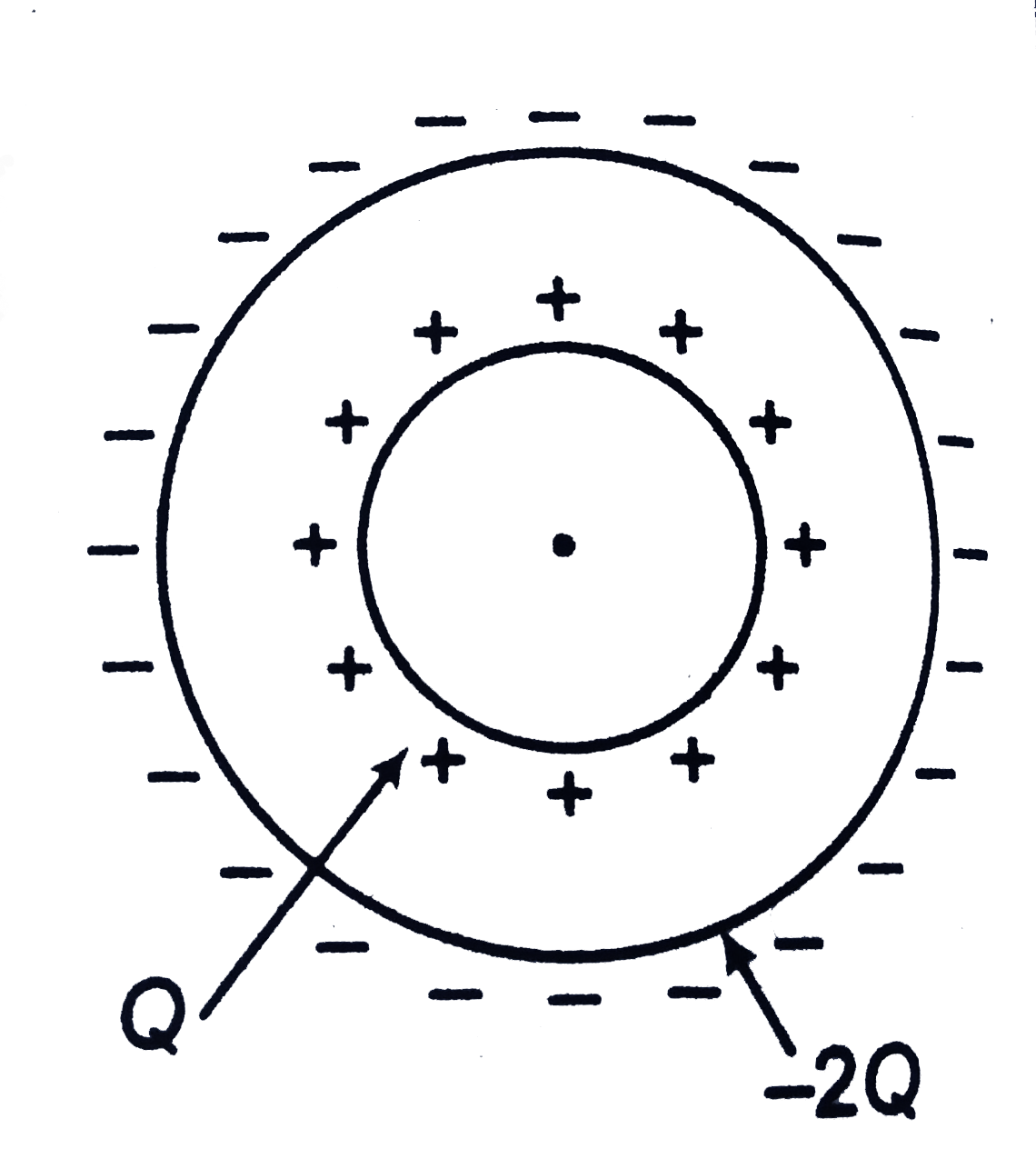
View SolutionTwo spheres of radius a and b respectively are charged and joined by a wire. The ratio of electric field of the spheres is
View SolutionA copper cylindrical tube has inner radius a and outer radius b. The resistivity is ρ. The resistance of the cylinder between the two ends is
View Solution