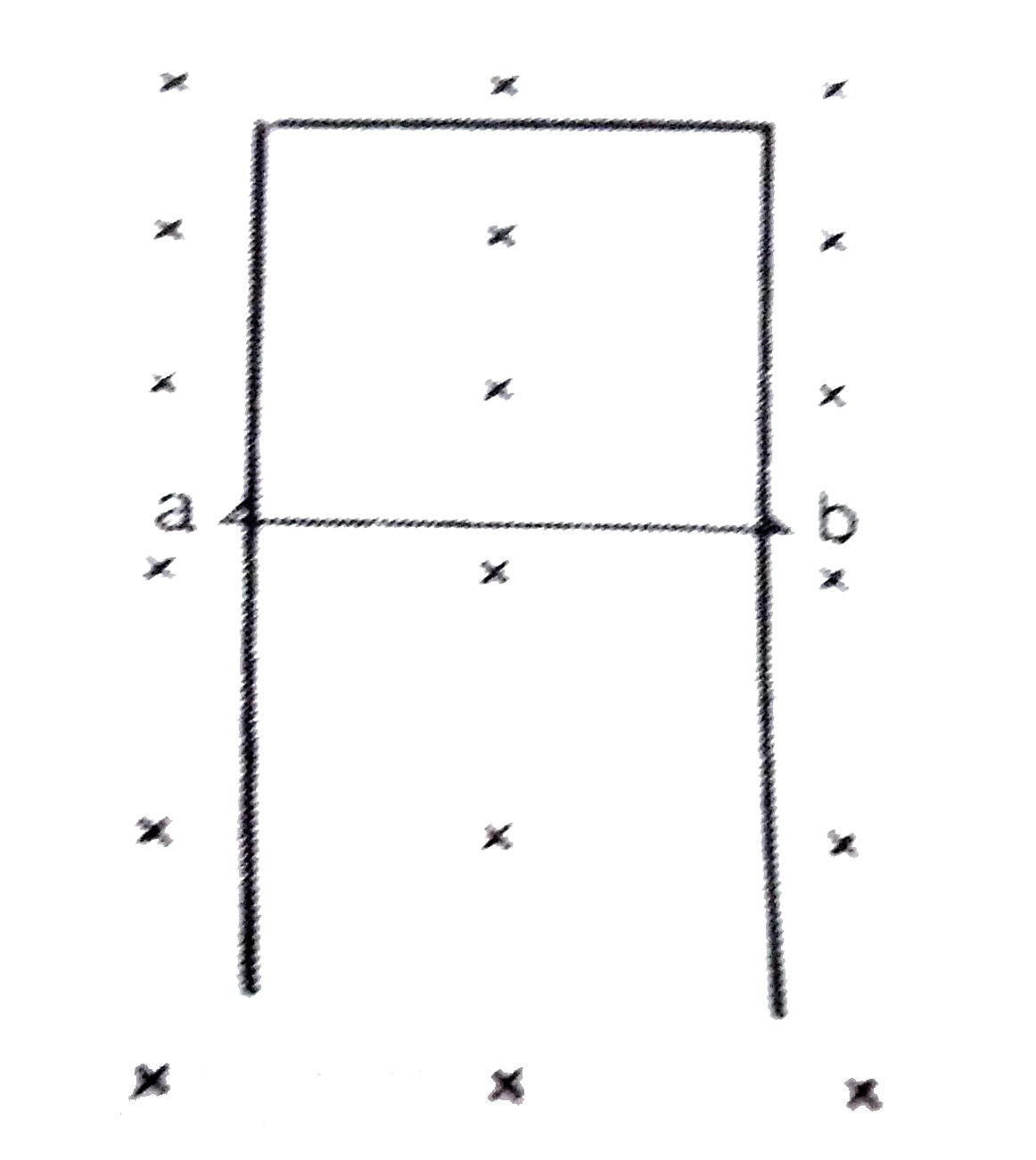
A metal bar with length , mass and resistance is polaced on frictionless metal rails that are inclined at an angle above the horizontal. The rails have negiligible resistance. There is a uniform magnetic field of nagnitude direction download in the figure. The bar is released from rest and slide down the rails.
(a) Is the direction of the current induced in the bar from and or to ?
(b) What is the terminal speed of the bar ?
What is the induced current in the bar when the terminal speed has been reached ?
(d) After the terminal speed has been reached, at what rate is electrical energy being converted to thermal energy in the resistance of the bar ?
(e) After the terminal speed has been reached, at what rate is work being done on the bar by gravity? Compare your answer to that in part (d).
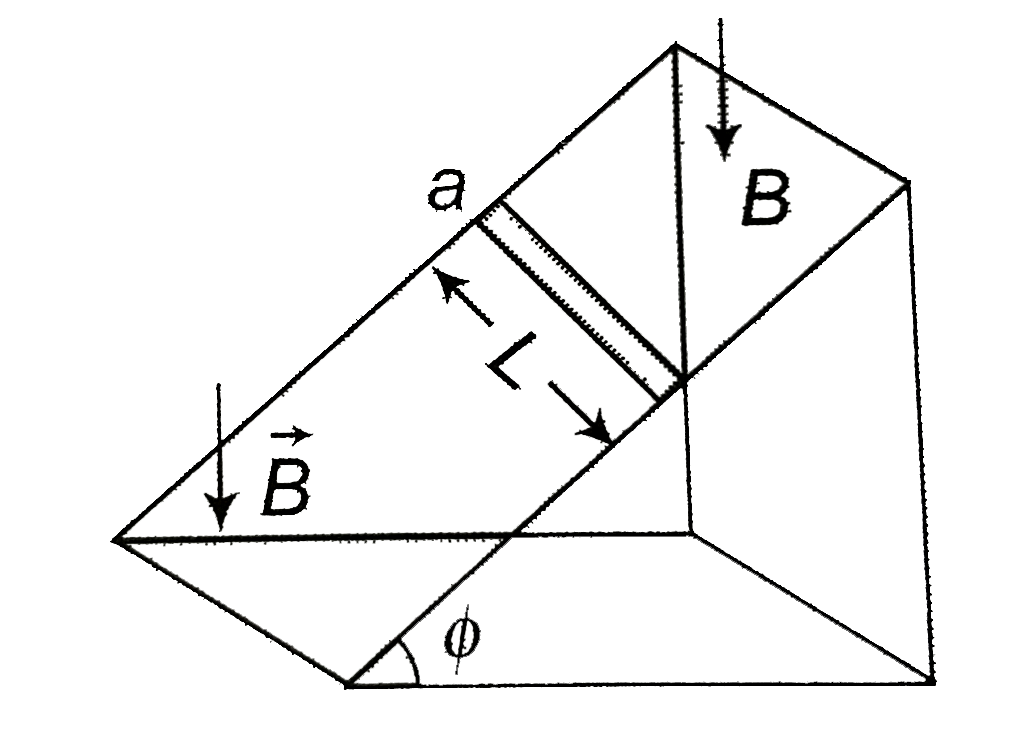
As bar slides down, flux through close area increases and hence magnetic field due to inducet current is upward therefore induced current is anticlockwise i.e. to .
(b) When speed of bar is
Induced emf
Induced current
Magnetic force due to
, along the plane upwards
, along
When velocity is constant i.e. net force=0
Terminal speed
(c)
(d)
Rate of work done by gravitational force


Topper's Solved these Questions
Similar Questions
The direction of induced current in the loop
 07:20View Solution
07:20View SolutionIn an atom, an electron moves in an orbit of radius r with a speed v, the equivalent current is.
03:24View SolutionWhich of the following is correct regarding electromagnetic wave?
03:24View SolutionTwo parallel vertical metallic rails AB and CD are separated by 1m. They are connected at the two ends by resistances R1 and R2 as shown in the figure. A horizontal metallic bar l of mass 0.2kg slides without friction, vertically down the rails under the action of gravity. There is a uniform horizontal magnetic field of 0.6T perpendicular to the plane of the rails. It is observed that when the terminal velocity is attained, the powers dissipated in R1 and R2 are 0.76W and 1.2W respectively (g=9.8m/s2)
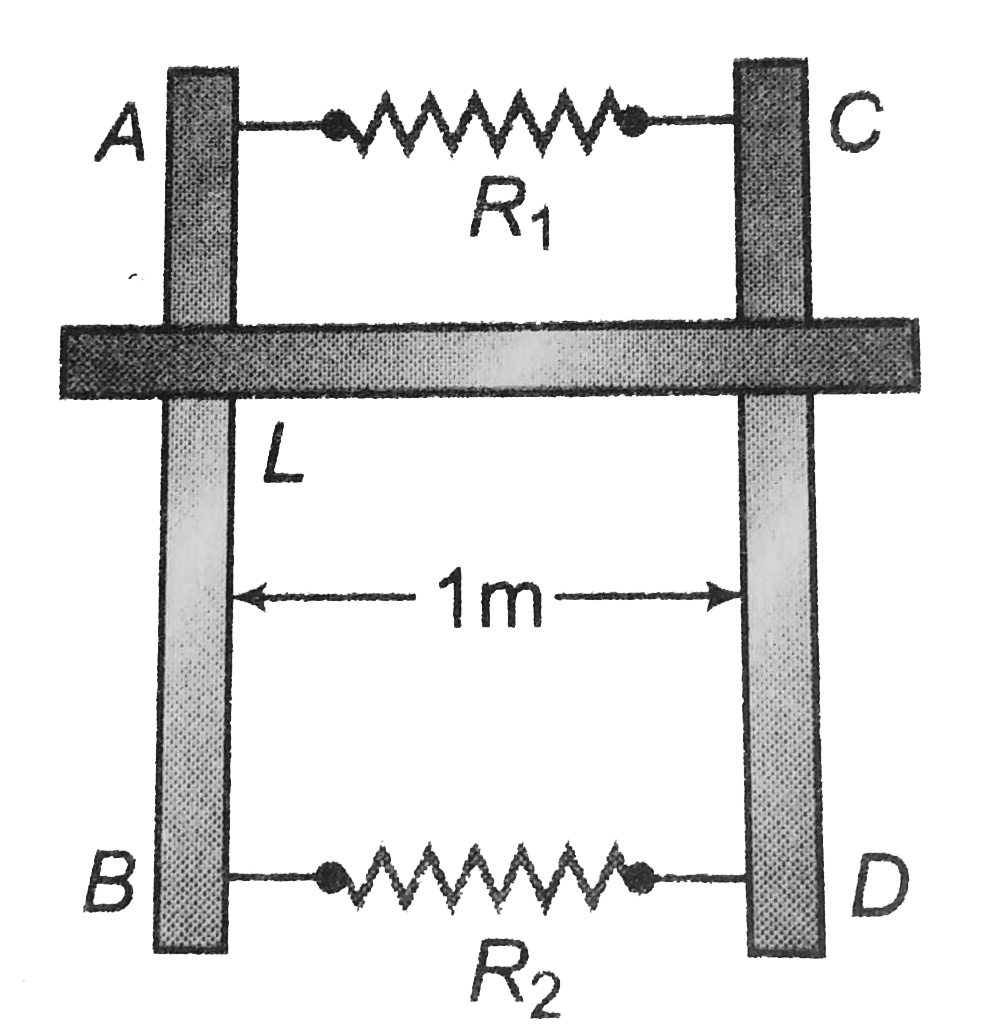
The terminal velocity fo the bar L will be05:32View SolutionA conductor bar with mass m and length L slides over horizontal rails that are connected to a voltage source. The voltage source maintains a constant current I in the rails and bar, and constant, uniform, vertical magnetic field →B fills the region between the rails (as shown in Fig.)

Find the magnitude and direction of the net force on the conducting bar. Ignore friction, air resistance and electrical resistance.06:52View SolutionA conductor bar with mass m and length L slides over horizontal rails that are connected to a voltage source. The voltage source maintains a constant current I in the rails and bar, and constant, uniform, vertical magnetic field vecB fills the region between the rails (as shown in Fig.) If the bar has mass m, find the distance d that the bar must move along the rails from rest to attain speed v.
06:24View SolutionA rod of mass m , length l and resistance R is sliding down on a smooth inclined parallel rails with a cinstant velocity v . If a uniform horizontal magnetic field B exists, then find thevalue of B .
04:47View SolutionA bar of mass m and length l moves on two frictionless parallel rails in the presence of a uniform magnetic field directed into the plane of the paper. The bar is given and initial velocity v_(i) to the right and released. Find the velocity of bar, induced emf across the bar and the current in the circuit as a function of time
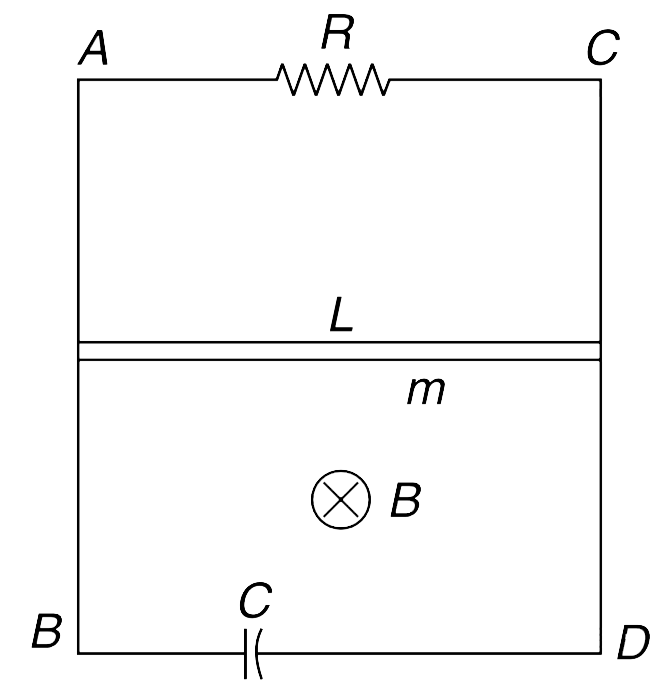
View SolutionTwo long fixed parallel vertical conducting rails AB and CD are separated by a distance L. They are connected by resistance R and a capacitance C at two ends as shown in the figure. There is a uniform magnetic field B directed horizon- tally into the plane of the figure. A horizontal metallic bar of length L and mass m can slide without friction along the rails. The bar is released from rest at t = 0. Neglect resistance of bar and rails and also neglect the self inductance of the loop.
(a) Find the maximum speed acquired by the bar after it is released.
(b) Find the speed of the bar as a function of time t.
 03:32View Solution
03:32View SolutionA straight horizontal conductor PQ of length l, and mass_ m slides down on two smooth conducting fixed parallel rails, set inclined at an angle 9 to the horizontal as shown in figure-5.30.
 The top end of the bar are connected with a capacitor of capacitance C. The system is placed in a uniform magnetic field, in the direction perpendicular to the inclined plane formed by the rails as shown in figure. If the resistance of the bars and the sliding conductor are negligible calculate the acceleration of sliding conductor as a function of time ifit is released from rest at t= 007:51View Solution
The top end of the bar are connected with a capacitor of capacitance C. The system is placed in a uniform magnetic field, in the direction perpendicular to the inclined plane formed by the rails as shown in figure. If the resistance of the bars and the sliding conductor are negligible calculate the acceleration of sliding conductor as a function of time ifit is released from rest at t= 007:51View SolutionA copper wire ab of length l, resistance r and mass m start sliding at t=0 down a smooth, vertical, thick pair of connected conducting rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct .
 View Solution
View SolutionA conducting rod ab of length l, mass m and resistance R slides on a smooth, thick pair of metallic rails. The plane of the rails makes an angles theta with the horizontal. A magnetic field B acts along the perpendicular to the horizontal plane in upward direction. If the rod slides down on the rails at a constant speed v, then show that B=sqrt((mgRsintheta)/(l^(2)vcos^(2)theta)) .
07:43View SolutionA wire ab of length l, mass m and resistance R slides on a smooth thick pair of metallic rails joined at the bottom as shown in fig. The plane of the rails makes an angle theta with the horizontal. A vertical magnetic field B exist in the region. If the wire slides on the rails at a constant speed v, then the value of B is -
02:48View SolutionA bar of mass m and length I moves on two frictionless parallel rails in the presence of a uniform magnetic field directed into the plane of the paper. The bar is given an initial velocity v to the right and released. Find the velocity of bar, induced emf across the bar and the current in the circuit as a function of time.
 02:08View Solution
02:08View SolutionTwo parallel vertical metallic rails AB and CD are separated by 1m. They are connected at the two ends by resistances R1 and R2 as shown in the figure. A horizontal metallic bar l of mass 0.2kg slides without friction, vertically down the rails under the action of gravity. There is a uniform horizontal magnetic field of 0.6T perpendicular to the plane of the rails. It is observed that when the terminal velocity is attained, the powers dissipated in R1 and R2 are 0.76W and 1.2W respectively (g=9.8m/s2)

The terminal velocity fo the bar L will be04:59View Solution

