A conducting rod ab of length l, mass m and resistance R slides on a smooth, thick pair of metallic rails. The plane of the rails makes an angles θ with the horizontal. A magnetic field B acts along the perpendicular to the horizontal plane in upward direction. If the rod slides down on the rails at a constant speed v, then show that B=√mgRsinθl2vcos2θ.
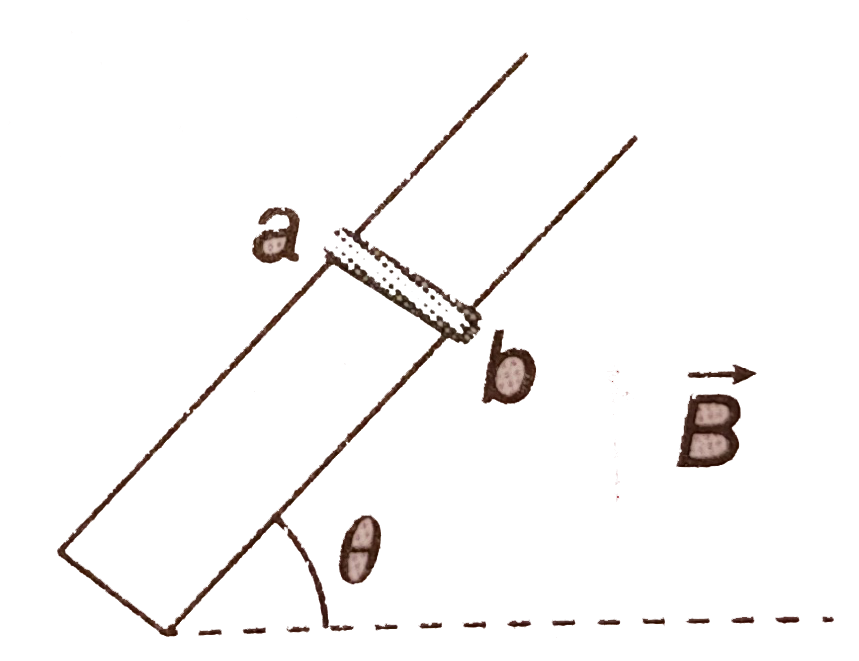 Solution in Bengali
Solution in Bengali
During the sliding of the rod with constant speed, the net force acting on the rod is zero.
∴Fmcosθ=mgsinθ
or, BIlcosθ=mgsinθ
or, mgsinθ=B(BlvcosθR)lcosθ
or, mgsinθ=B2l2vcos2θR
or, B2=mgRsinθl2vcos2θ
∴B=√mgRsinθl2vcos2θ
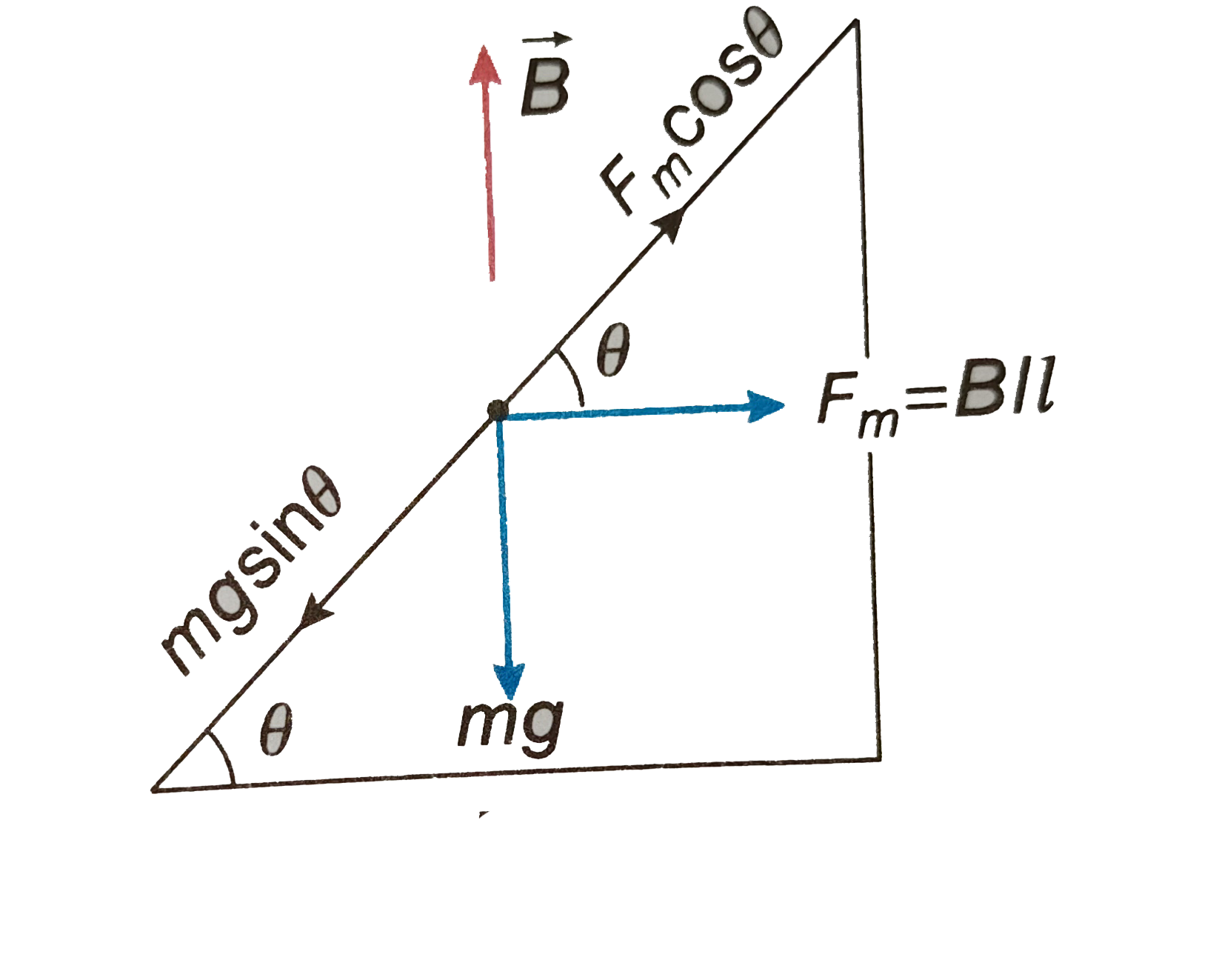
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - NCERTS TEXTBOOK QUESTIONS WITH ANSWER HINT
21 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - NCERT EXEMPLAR QUESTIONS WITH ANSWER HINT (MCQ-1)
5 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - SECTION RELATED QUESTIONS
29 Videos
- ELECTRIC POTENTIAL BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC POTENTIAL EXERCISE - CBSE Scanner
13 Videos
- ELECTROMAGNETIC WAVES BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - CBSE SCANNER
17 Videos
Similar Questions
Use Lenz's law to determine the direction of induced current in the situations described in the figure :

A wire of irregular shape turning into a circular shape.
View SolutionA cylinder bar magnet is rotated about its axis. A wire is connected from the axis and is made to touch the cylindrical surface through a contact. Then

View SolutionWhat do you mean by electromagnetic induction?
View SolutionA test charge q is moved without acceleration along the path from A to B from B to C in electric field E as shown in fig.

(i) Calculate the potential difference between A and C.
View SolutionWhat are the directions of electric and magnetic field vectors relative to each other and relative to the direction of propagation of electromagnetic waves?
View SolutionA rod of mass m , length l and resistance R is sliding down on a smooth inclined parallel rails with a cinstant velocity v . If a uniform horizontal magnetic field B exists, then find thevalue of B .
View SolutionA copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle theta to the horizontal. At the bottom, the rails are joined by a resistance R . There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod is
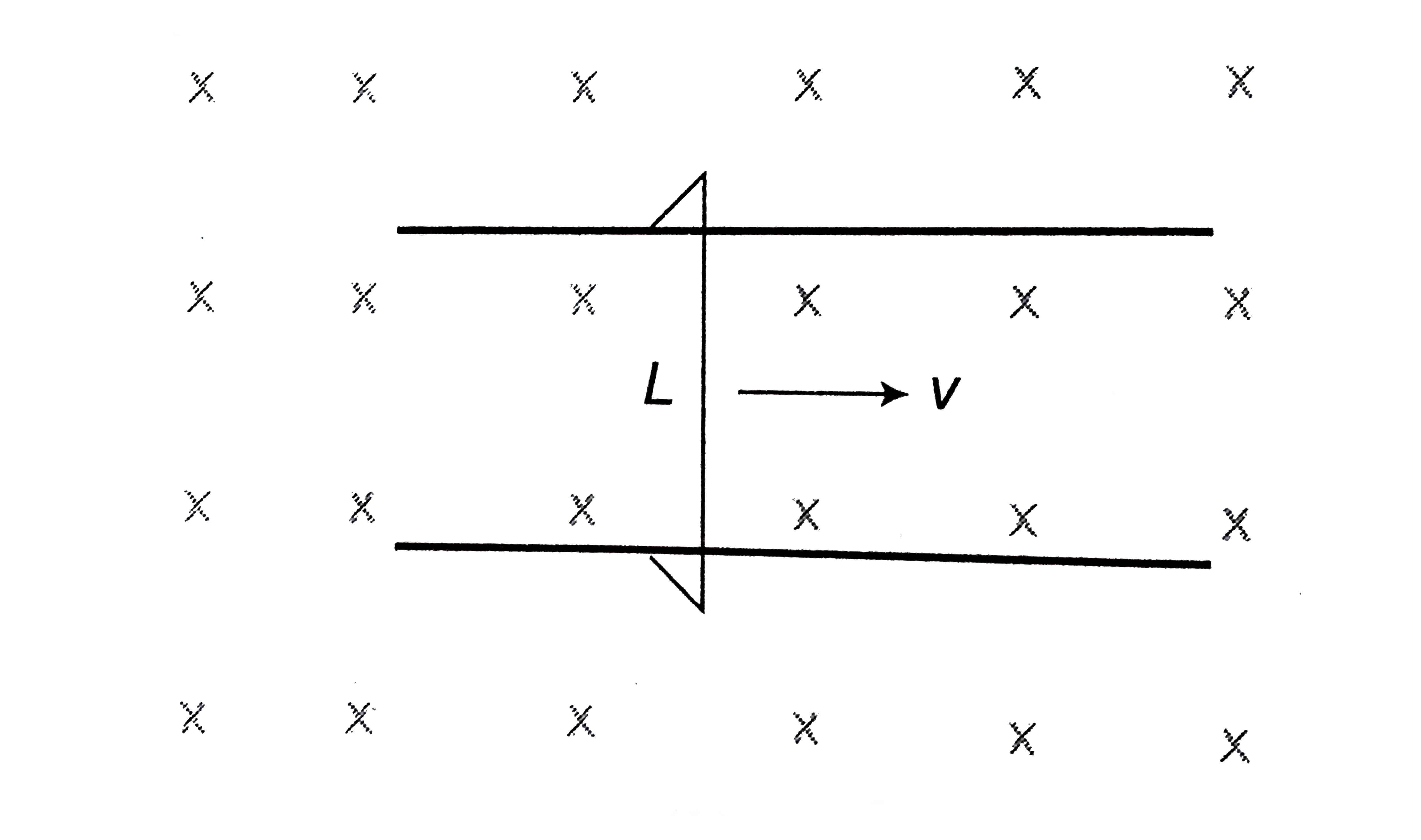
View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
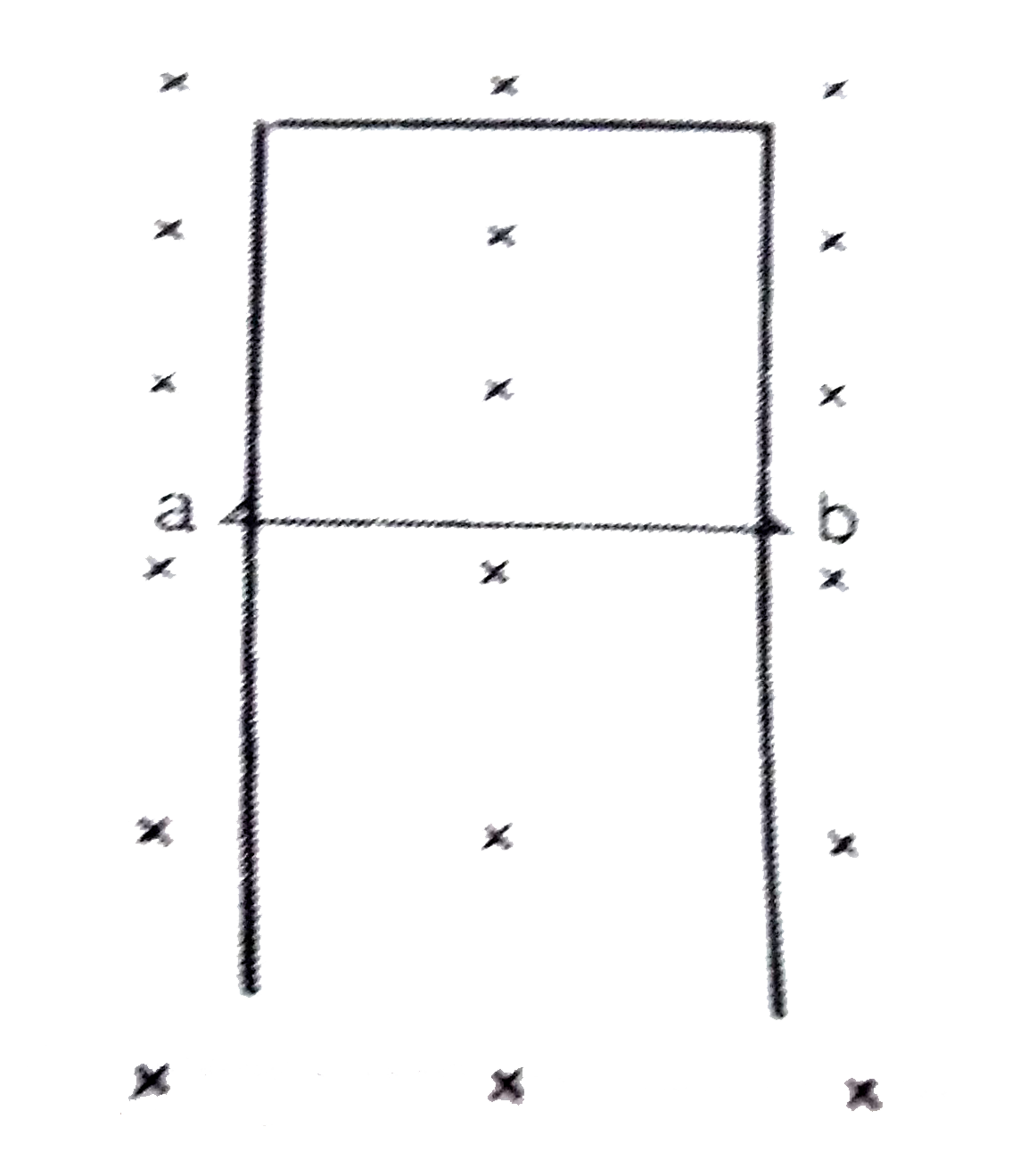
View SolutionA copper wire ab of length l, resistance r and mass m starts sliding at t=0 down a smooth, vertical, thick pair of connected condcuting rails as shown in figure.A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct.
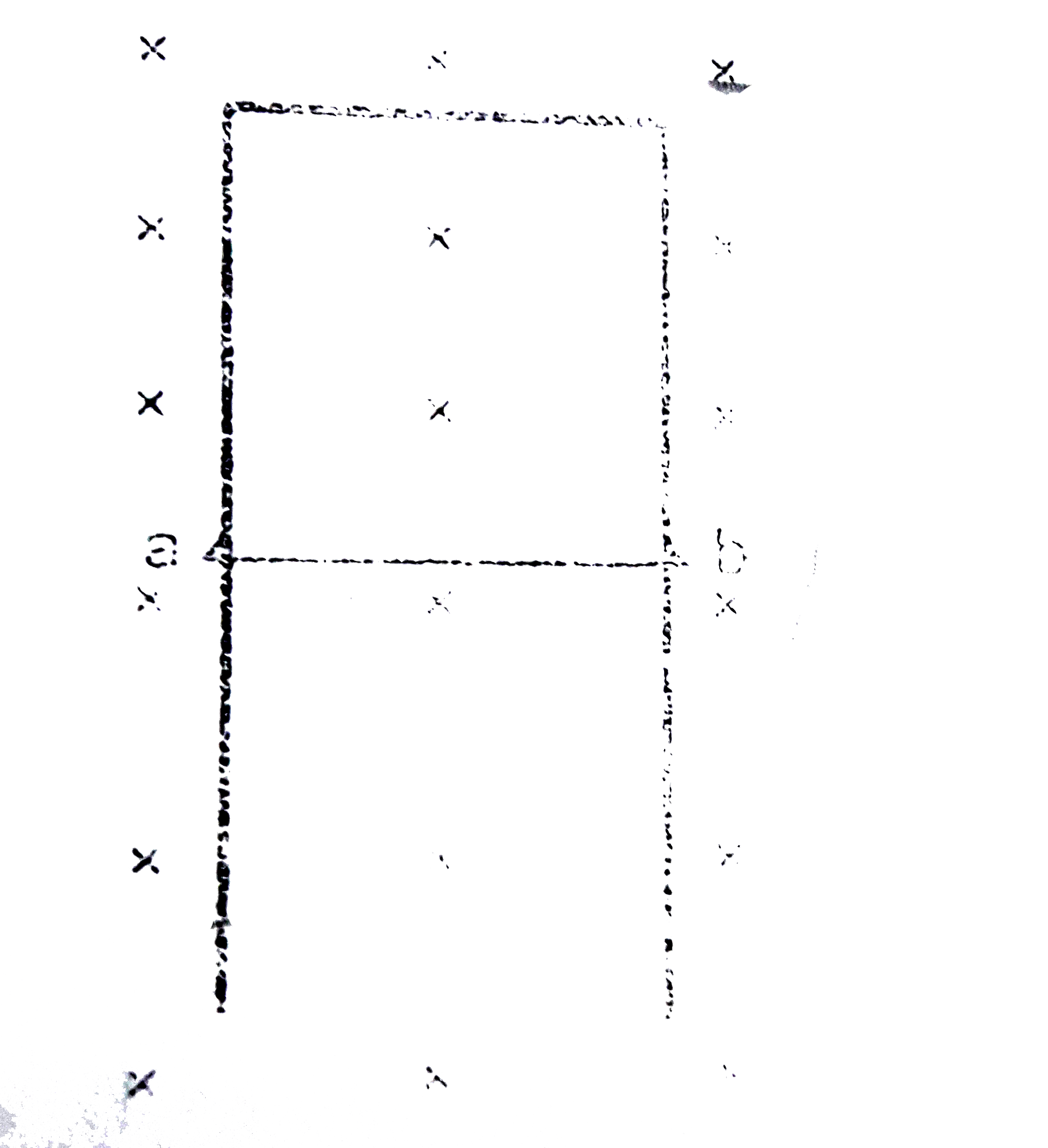
View SolutionA copper wire ab of length l, resistance r and mass m start sliding at t=0 down a smooth, vertical, thick pair of connected conducting rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct .
View Solution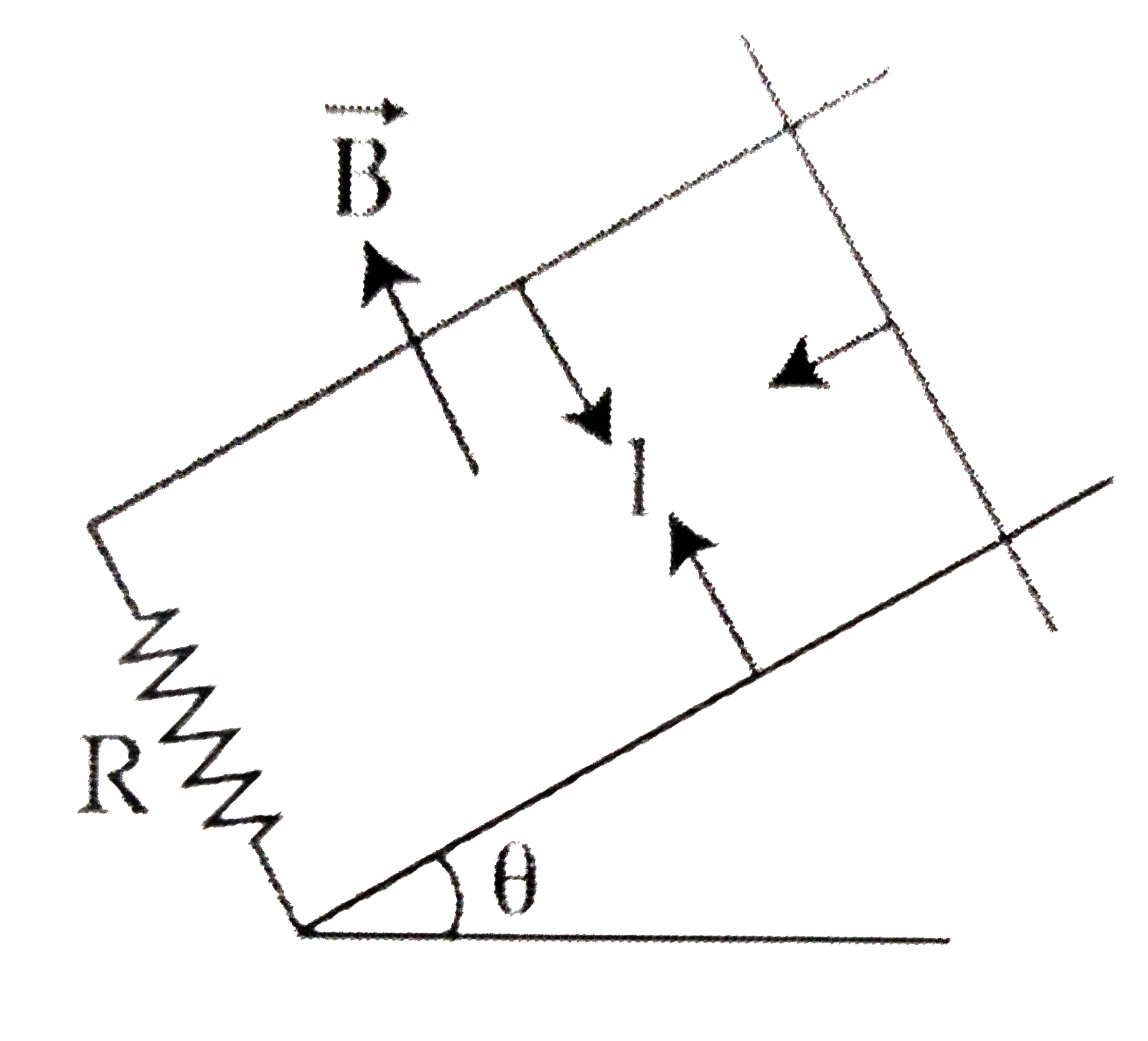
a copper rod of mass m slides under gravity on two smooth parallel rails with separation I and set at an angle of θ with the horiziontal at the bottom rails are joined by resistance R. There is a uniform magnetic field B normal to the plane of the rails as shown in the figure The terminal speed of the copper rod is :
View SolutionA wire ab of length l, mass m and resistance R slides on a smooth thick pair of metallic rails joined at the bottom as shown in fig. The plane of the rails makes an angle theta with the horizontal. A vertical magnetic field B exist in the region. If the wire slides on the rails at a constant speed v, then the value of B is -
View Solutionएक कॉपर की छड़ का द्रव्यमान m है। यह दो क्षैतिज समान्तर चिकनी पटरियों (rails) जिनके बीच की दूरी । है तथा क्षैतिज के साथ θ कोण बनाती है, पर गुरुत्व के अन्तर्गत फिसलती है। तली में पटरियाँ एक प्रतिरोध R के द्वारा चित्रानुसार जुड़ी हैं। यहाँ एकसमान चुम्बकीय क्षेत्र B पटरियों (rails) के तल के लम्बवत् है। छड़ का क्रान्तिक वेग है

View SolutionA wire ab of length l, mass m and resistance R slided on a smooth, thick pair of metallic rails joined at the bottom as shown in . The plane of the the rails makes an angle theta with the horizontal. A vertical magnetic field B exists in the ragion. if the wire slides on the rails at a constant speed v, show that B = sqrt(mg R sin theta)/(vl^2 cos^theta) .
View Solutiona copper rod of mass m slides under gravity on two smooth parallel rails with separation I and set at an angle of theta with the horiziontal at the bottom rails are joined by resistance R. There is a uniform magnetic field B normal to the plane of the rails as shown in the figure The terminal speed of the copper rod is :
View Solution
