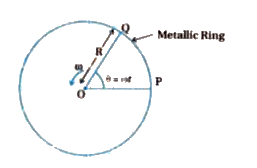
A metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular to the plane of the ring as per figure. A constant and uniform magnetic field of 1T parallel to the axis is present everywhere. What is the emf between the centre and the metallic ring ?
Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

Consider uniform magnetic field $\to B (x)$ , perpendicularly inside the plane of figure. Also consider a metallic ring of radius R whose plane is perpendicular to $\to B$ . There is a conducting rod (OQ) of length R, with its one end hinged at O (centre of ring) and another end in contact with the ring. Suppose, this rod rotates anticlockwise with constant angular speed $ω$ . Because of this motion of rod, free electrons in it acquire velocity $\to v ⊥ \to B$ and hence they are exerted upon by magnetic force ${\to F}_{m} = e (\to B \times \to v)$ in a direction from centre to outer end. Hence, free electrons in the rod start displacing away from centre, making centre positive and outer end negative. After some time when electric force ${\to F}_{e}$ exerted on free electrons becomes equal and opposite to magnetic force ${\to F}_{m}$ , a steady state is reached when Lorentz force exerted on electrons becomes zero. At this stage, we get maximum induced emf across the two ends of rod (or between centre and periphery of ring). Let this emf be $ε$ whose formula can be derived as follows.
Across the elemental length dr of rod chosen at distance r from centre if induced emf is $d ε$ then according to formula of motional emf we can write,
$d ε = B v d r$
$∴ d ε = B (r ω) d r$
$∴$ Total induced emf across the rod will be ,
$ε = \int d ε$
$= \int B (r ω) d r$
$= B ω \int_{0}^{R} r d r$
$∴ ε = B ω {\frac{r^{2}}{2}}_{0}^{R}$
$∴ ε = \frac{1}{2} B ω R^{2}$
Second Method : In above figure, suppose the rod rotates by extremely small angle $d θ$ in time dt. Here, length of arc $Q Q . = R d θ$ . Now, area traversed (or swept) by rod in time dt would be
$d A = \frac{1}{2}$ (base)(height)
$= \frac{1}{2} (R) (R d θ)$
$d A = \frac{1}{2} R^{2} d θ$
Magnetic flux cut by the rod in time dt is ,
$d ϕ = B (d A)$
$∴ d ϕ = B (\frac{1}{2} R^{2} d θ)$
$∴ \frac{d ϕ}{d t} = \frac{1}{2} B R^{2} \frac{d θ}{d t}$
$∴ \frac{d ϕ}{d t} = \frac{1}{2} B R^{2} ω$ ( $∵ ω = \frac{d θ}{d t}$ = constant angular speed of rod )
Now, induced emf across the rod will be ,
$ε = - \frac{d ϕ}{d t}$
$∴ ε = - \frac{1}{2} B ω R^{2}$
$∴ | ε | = \frac{1}{2} B ω R^{2}$
Third Method :
At time t=0 , $ε_{1} = 0 (∵ v = 0 \Rightarrow ε = B v l = 0)$
At time t=t, $ε_{2} = B v l$ ( $∵$ For l=R, $(v = R ω)$ )
$= B (R ω) R$
$ε_{2} = B ω R^{2}$
$∴$ Average induced emf
$< ε > = \frac{ε_{1} + ε_{2}}{2} = \frac{0 + B ω R^{2}}{2}$
$∴ < ε > = \frac{1}{2} B ω R^{2}$
Now , value of induced emf across the rod in the present situation will be ,
$ε = \frac{1}{2} B ω R^{2}$
$= \frac{1}{2} B (2 π f) R^{2}$ ( $∵ ω = 2 π f$ where f=frequency of rotation)
$= (1) (3.14) (50) {(1)}^{2}$
$∴ ε$ =157 V

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-ELECTROMAGNETIC INDUCTION-Section B (Numerical) Textual Illustrations

Home
Ask Doubt
Profile