A meter stick of negligible mass can rotate about a vertical axis through a point at distant x from the point marked "0". A small block of mass 0.100 kg is glued at the mark of "0" and a small block of mass 0.500 kg is glued at the opposite end, at the mark of "1." The stick and blocks are to rotate with an angular speed of 5.00 rad/min. (a) For what choice of x is the associated rotational kinetic energy least and (b) what is that least erergy?
To solve the problem, we will break it down into steps for both parts (a) and (b).
1. Understanding the System:
- We have a meter stick with two blocks:
- Block 1 (mass m1=0.1kg) at position 0.
- Block 2 (mass m2=0.5kg) at position 1 meter.
- The stick rotates about a vertical axis at a distance x from the point marked "0".
2. Moment of Inertia (I):
- The moment of inertia I of the system can be expressed as:
I=m1x2+m2(1−x)2
- Substituting the values of m1 and m2:
I=0.1x2+0.5(1−x)2
3. Expanding the Moment of Inertia:
- Expand I:
I=0.1x2+0.5(1−2x+x2)=0.1x2+0.5−x+0.5x2
- Combine like terms:
I=(0.1+0.5)x2−x+0.5=0.6x2−x+0.5
4. Finding the Minimum of I:
- To find the value of x that minimizes I, we take the derivative of I with respect to x and set it to zero:
dIdx=1.2x−1=0
- Solving for x:
1.2x=1⟹x=11.2=56≈0.833m
5. Conclusion for Part (a):
- The value of x that minimizes the rotational kinetic energy is approximately 0.833m.
Part (b): Calculating the least rotational kinetic energy
1. Calculating the Moment of Inertia at x=56:
- Substitute x=56 into the moment of inertia formula:
I=0.6(56)2−(56)+0.5
- Calculate I:
I=0.6⋅2536−56+0.5=1536−3036+1836=336=112kg m2
2. Calculating the Rotational Kinetic Energy:
- The rotational kinetic energy KE is given by:
KE=12Iω2
- Convert ω=5rad/min to rad/s:
ω=560rad/s=112rad/s
- Substitute I and ω into the kinetic energy formula:
KE=12⋅112⋅(112)2=12⋅112⋅1144=12⋅11728=13456J
3. Final Calculation:
- The least rotational kinetic energy is approximately:
KE≈2.9×10−4J
Final Answers:
- (a) The value of x for minimum rotational kinetic energy is 0.833m.
- (b) The least rotational kinetic energy is approximately 2.9×10−4J.
- We have a meter stick with two blocks:
- Block 1 (mass m1=0.1kg) at position 0.
- Block 2 (mass m2=0.5kg) at position 1 meter.
- The stick rotates about a vertical axis at a distance x from the point marked "0".
- The moment of inertia I of the system can be expressed as:
I=m1x2+m2(1−x)2
- Substituting the values of m1 and m2:
I=0.1x2+0.5(1−x)2
- Expand I:
I=0.1x2+0.5(1−2x+x2)=0.1x2+0.5−x+0.5x2
- Combine like terms:
I=(0.1+0.5)x2−x+0.5=0.6x2−x+0.5
- To find the value of x that minimizes I, we take the derivative of I with respect to x and set it to zero:
dIdx=1.2x−1=0
- Solving for x:
1.2x=1⟹x=11.2=56≈0.833m
- The value of x that minimizes the rotational kinetic energy is approximately 0.833m.
- Substitute x=56 into the moment of inertia formula:
I=0.6(56)2−(56)+0.5
- Calculate I:
I=0.6⋅2536−56+0.5=1536−3036+1836=336=112kg m2
- The rotational kinetic energy KE is given by:
KE=12Iω2
- Convert ω=5rad/min to rad/s:
ω=560rad/s=112rad/s
- Substitute I and ω into the kinetic energy formula:
KE=12⋅112⋅(112)2=12⋅112⋅1144=12⋅11728=13456J
- The least rotational kinetic energy is approximately:
KE≈2.9×10−4J
- (a) The value of x for minimum rotational kinetic energy is 0.833m.
- (b) The least rotational kinetic energy is approximately 2.9×10−4J.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)43videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)7videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT18videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)5videos
RELATIVITY
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)2videos
RIGID BODY DYNAMICS-II
Similar Questions
A wooden block of mass 0.8 kg is dragged along a level frictionless surface by a hanging block of mass 0.2 kg as shown in the figure. Calculate the tension in the string and the acceleration of blocks.
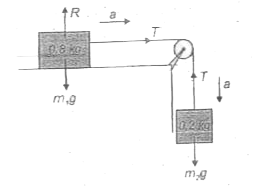 View Solution
View SolutionA wooden block of mass 0⋅8 kg is dragged along a level frictionless surface by a hanging block of mass 0⋅2 kg as shown in the figure . Calculate the tension in the string and the acceleration of blocks .
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A flywheel having a radius of gyration of 2m and mass 10 kg rotates at an angular speed of 5rads−1 about an axis perpendicular to it through its centre. The kinetic energy of rotation is
A500 JB2000 JC1000 JD250 J - Question 2 - Select One
A block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block through another string. Find the tensions in the two strings. Take g=10ms2.
AT1=3N,T2=5NBT1=4N,T2=3NCT1=5N,T2=5NDT1=3N,T2=3N - Question 3 - Select One
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad/s. The radius of the cylinder is 0.25 m. The kinetic energy associated with the rotation of the cylinder is
A3025 JB3225 JC3250 JD3125 J
A block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block through another string. Find the tensions in the two strings. Take g=10ms2.
View SolutionA thread is passing through a hole at the centre of frictionless table. At the upper end a block of mass 0.5kg is tied and a block of mass 8.0kg is tied at the lower end which is freely hanging. The smaller mass is rotate, on the table with a constant angular velocity about the axis passing through the hole so as to balance the heavier mass. If the mass of the hanging block is changed from 8.0kg to 1.0kg, what is the fractional change in the radius and the angular velocity of the smaller mass so that it balances the hanging mass again?
 View Solution
View SolutionA uniform rod of length 1m and mass 0.5kg rotates at angular speed of 6rad/sec about one of its ends. What is the KE (in joule) of the rod ?
View SolutionA block of mass 0.50 kg is moving with a speed of 2.00 m/s on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
View SolutionAn solid cylinder of mass 20kg and radius 20cm rotates about its axis with a angular speed 100rads−1. The angular momentum of the cylinder about its axis is.
View Solution

