A metre scale is standing vertically on a horizontal table on one of its end. It now falls on the table without slipping. The velocity with which the free end of the metre scale strikes the table is
[Given I=mL23]
9.8 m/s
1 m/s
4.5 m/s
5.4 m/s
The correct Answer is:D
Loss in P.E. =Gain in K.E.
∴mgh=12Iω2=12ML23ω2
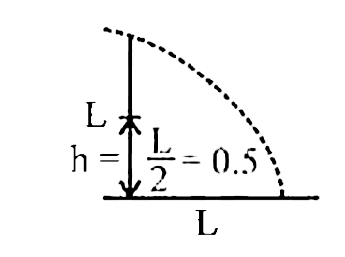
∴g×0.5=12×13×12×ω2
∴ω=√3g=√3×9.8=√29.4=5.4
∴v=rω=1×ω=1×5.4=5.4m/s
Topper's Solved these Questions
Similar Questions
Knowledge Check
A metre scale of mass M is standing vertically on a horizontal table on one of its ends. It now falls on the table without slipping. The velocity with which the free end of the metre scale strikes the table is
[Given : I=ML23 and g=10m/s2 ]A√20m/sB√15m/sC√30m/sD√10m/sA metre scale is suspended vertically from a horizontal axis passing through one end of it. Its time period would be
A1.64 secB2 secC2.5 secD3.2 secA rod length 15 m stands vertically on the ground. With one end hinged to the ground. When it falls on the ground such that it rotates without slipping, the velocity of the upper tip on striking the ground is
A15 m/sB15√2m/sC15√2m/sD15√3m/s
A thin metal rod of length 0.5m is vertically straight on horizontal floor. This rod is falling freely to a side without slipping. The angular velocity of rod when its top end touches the floor is (nearly)
View SolutionA thin rod of length L is vertically straight on horizontal floor. This rod falls freely to one side without slipping of its bottom. The linear velocity of centre of rod when its top end touches floor is
View SolutionA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
View SolutionA uniform chain of length l is placed on a smooth horizontal table, such that half of its length hangs over one edge. It is releasedfrom rest, the velocity with which it leaves the table is
View SolutionA metre scale of mass 200 g, is lying on a horizontal table. What is the work done by student in making it stand vertically on one of its ends?
View Solution
