A monkey of mass m clings a rope to a slung over a fixed pulley .The opposite end of the rope is tried to a weight of mass M tying on a horizontal table is μ Find the acceleration of weight and the tension of the rope for two cases .The monkey move downward with respect to the rope with an acceleration b.

The tension of rope is
Mm(μg+g+b)M+m
Mm(μg−g+b)M+m
Mm(μg+g−b)M+m
Mm(μg−g−b)M+m
The correct Answer is:c
As the monkey move downward with respect to rope with an acceleration b. absulute acceleration is a+b, where a is the acceleration of rope, Therefore equation of motion are
mg−T=m(a+b)…(i)
T−μMg=Ma…(ii)
Putting the value of T from Eqs(ii) and (i) we get
(m−μM)g=(M+m)a+mb
⇒m(g−b)−μMg(M+m)=a
T=μMg+Mmg−Mmb−μM2gM+m
=μM2g+μMmg+Mmg−Mmb−μM2gM+m
=Mm(μg+g−b)M+m
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer
6 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - True And False
4 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A monkey of massm clings to a rope slung over a fixed pulley. The opposite end of the rope is tied to a weight of
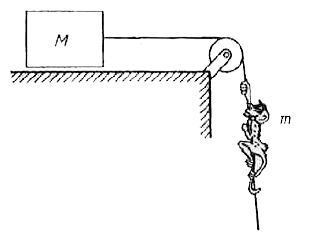
mass M lying on a horizontal plat (Fig.). Neglecting friction find the acceleration of both bodies (relative to the plate) and the tension of the rope for the three cases:
(1) the monkey does not move with respect to the rope,
(2) the monkey moves upwards with respect to the rope with acceleration b,
(3) the monkey moves downwards with respect to the rope with an acceleration b.
View SolutionA monkey of mass m climbs up to a rope hung over a fixed pulley. The opposite end of the rope is tied to a weight of mass M lying on a horizontal plane. Neglecting the friction, find the acceleration of both the bodies (relative to the plane) and the tension of the rope for the three cases:
(i) The monkey does not move with respect to the rope
(ii) The monkey moves upwards with respect to the rope with acceleration a.
(iii) The monkey moves downwards with respect to the rope, with acceleration a.
View Solution
Knowledge Check
A monkey of mass m clings a rope to a slung over a fixed pulley .The opposite end of the rope is tried to a weight of mass M tying on a horizontal table is μ Find the acceleration of weight and the tension of the rope for two cases .The monkey move downward with respect to the rope with an acceleration b.

The acceleration of weight isA2m(g+b)−μMgM+2mBm(g+b)−μMg2(M+m)Cm(g+b)−3μMgM+3mDm(g+b)−μMgM+2mA cat of mass m = 1 kg climbs to a rope hung over a leight frictionless pulley. The opposite end of the rope is tied to a weight of mass M = 2m lying on a smooth horizontal plane. What is the tension of the rope where the cat move upwards with in acceleration a=2m/s2 relative to the rope ?
 A2 NB12NC8ND4N
A2 NB12NC8ND4NIn figure the tension in the rope (rope is light) is
 A(M+m)gsinθB(M+m)gsinθ−μmgcosθCZeroD(M+m)gsinθ
A(M+m)gsinθB(M+m)gsinθ−μmgcosθCZeroD(M+m)gsinθ
A monkey of mass 'm' climbs up to a rope hung over a fixed pulley with an acceleration g/4. The opposite end of the rope is tied to a block of mass M lying on a rough horizontal plane. The coefficient of friction between the block and horizontal plane is μ. Find the tension in the rope.

View SolutionA monkey of mass 'm' climbs up to a rope hung over a fixed pulley with an acceleration relative to the rope g/4. The opposite end of the rope is tied to a bock of mass M lying on a rough horizontal plane. The coeffient of friction between the block and horizontal plane is μ. Find the tension in the rope
View SolutionIf a monkey moves upward with respect to the rope with acceleration g/2 then acceleration of block, if masses of block and monkey are same
View SolutionConsider the arrangement shown in the figure. Find the acceleration of the block
(a) A monkey moves upward with respect to the rope with acceleration a0
(b) A monkey moves downward with respect to the rope with acceleration a0
Assume the surface smooth, pulley and string light.

View SolutionA 40 kg boy climbs a rope that passes over an ideal pulley. The other end of the rope is attached to a 60 kg weight placed on the ground. What is the maximum upward acceleration the boy can have without lifting the weight ? If he climbs the rope with upward acceleration 2 g, with what acceleration the weight will rise up ?
View Solution
