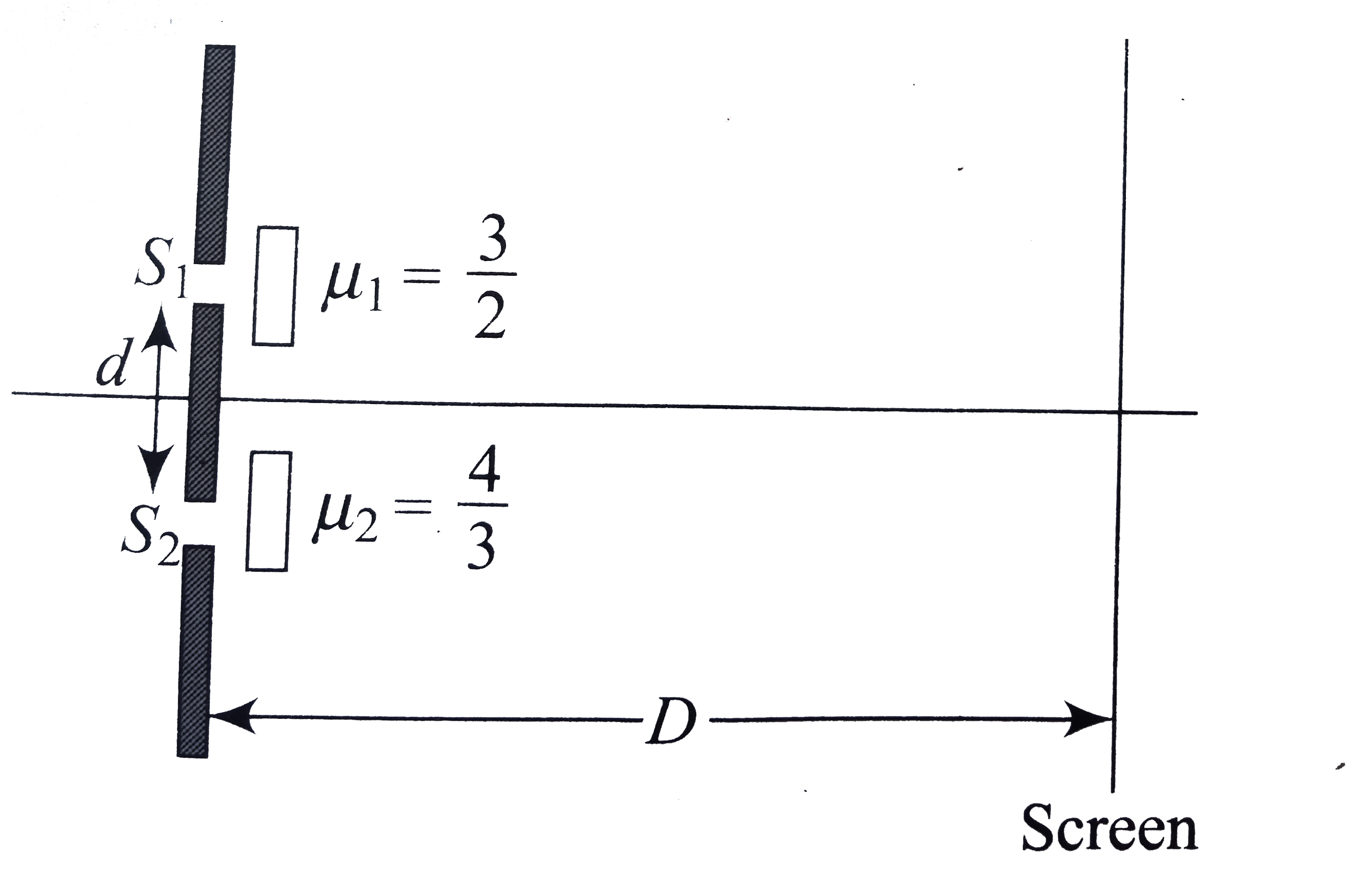
A monochromatic beam of light of 6000 Å is used in YDSE set-up. The two slits are covered with two thin films of equal thickness t but of different refractive indices as shown in figure. Considering the intensity of the incident beam on the slits to be I0, find the point on the screen at which intensity is I0 and is just above the central maxima. (Assume that there is no change in intensity of the light after passing through the films.) Consider t=6μm,d=1mm, and D=1m, where d and D have their usual meaning. Give your answer in mm.
The correct Answer is:y=30mm
I0=4I0cos2.ϕ2
⇒cos.ϕ2=12
⇒ϕ=2π3
Therefore, path difference of the two beams producing intensity I0 on the screen is λ/3.
Optical path difference between two beams meeting on the screen is
Δx={(S2P−t+43t)−(S1P−t+32t)}
=(S2P−S1P)+t(43−32)
Δx=dsinθ−t6
∴dyD−t6=λ3
⇒dyD=λ3+t6
⇒y=Dd[λ3+t6]
=110−3(6000×10−103+0.6×10−66)
=110−3×3×10−7=3×10−4m
∴y=30mm.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Single Correct
128 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.2
22 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
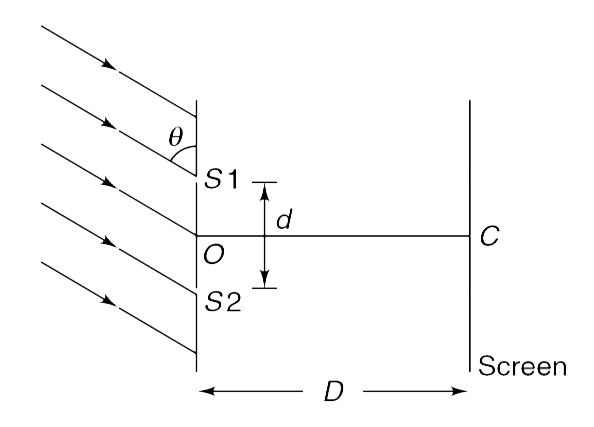
In a double slit experiment a parallel beam of light strikes the slit plane at an angleθ as shown in the figure. The two slits are covered with transparent plastic sheets of equal thickness t but of different refractive indices 1.2 and 1.5. The central maxima is formed at the centre of the screen at C.
(a) Which sheet was used to cover the slit S1?
(b) Findθ.
View SolutionIn Young's double slit experiment the two slits are illuminated with light of wavelength λ .The thickness of a film of refractive index 1.4 to be introduced in the path of one of the interfering beams so that the central image shifts by one fringe width is
View Solution
Knowledge Check
In the YDSE shown the two slits are covered with thin sheets having thickness t&2t and refractive index 2μand μ .Find the position (y) of central maxima.
 AzeroBtDdC−tDdDnone
AzeroBtDdC−tDdDnoneA thin perfectly transparent glass sheet of thickness t and refractive index mu is pasted on one of the two identical slits. If the intensity of light at the centre of the screen is I0 in the absence of glass sheet, the intensity at O as a function of thickness of the glass plate is
AI0cos(μtλ)BI0cos2(μtλ)CI0cos2(π(μ−I)tλ)DI0cos(π(μ−I)tλ)In a YDSE with identical slits, the intensity of the central bright fringe is I0. If one of the slits is covered, the intensity at the same point is
A2I0BI0CI0/2DI0/4
A thin glass plate of thickness t and refractive index μ is inserted between screen and one of the slits in a young's experiment. If the intensity at the centre of the screen is I, what was the intensity at the same point prior to the introduction of the sheet.
View SolutionIn the Young's double slit experiment the central maxima is observed to be I0. If one of the slits is covered, then intensity at the central maxima will become-
View SolutionIn YDSE of equal width slits, if intensity at the center of screen is I0, then intensity at a distance of β/4 from the central maxima is
View SolutionA monochromatic beam of light is used for the formation of fringes on a screen by illuminating the twoslits in the Young,s double slit interfrence experiment. When a thin film of mic is interposed in the path of one of the interfering beams
View SolutionIn a Young's double slit experiment the amplitudes of the two waves incident on the two slits are A and 2A. If I0 is the maximum intensity, then the intensity at a spot on the screen where the phase difference between the two interfering waves is ϕ .
View Solution
