A neutron and a proton both are fired with some speed of 3×106 m/s perpendicular to a uniform magnetic field of 1 T. What will be the individual acceleration of particles! Consider that only magnetic force is acting on the particles.
To find the individual acceleration of a neutron and a proton when fired perpendicular to a magnetic field, we will follow these steps:
Step 1: Understand the Forces Acting on the Particles
When charged particles move in a magnetic field, they experience a magnetic force given by the Lorentz force equation:
F=q(v×B)
where:
- F is the magnetic force,
- q is the charge of the particle,
- v is the velocity of the particle,
- B is the magnetic field.
Step 2: Calculate the Acceleration
The acceleration a of a particle can be calculated using Newton's second law:
a=Fm
Substituting the expression for the magnetic force into this equation gives:
a=q(v×B)m
Step 3: Determine the Charge and Mass of Each Particle
- For the neutron:
- Charge qn=0 (neutrons are neutral).
- Mass mn≈1.67×10−27 kg.
- For the proton:
- Charge qp=1.6×10−19 C.
- Mass mp≈1.67×10−27 kg.
Step 4: Calculate the Acceleration of the Neutron
Since the neutron has no charge:
an=qn⋅v⋅Bmn=0⋅(3×106)⋅11.67×10−27=0
Thus, the acceleration of the neutron is:
an=0m/s2
Step 5: Calculate the Acceleration of the Proton
For the proton:
ap=qp⋅v⋅Bmp
Substituting the values:
ap=(1.6×10−19)⋅(3×106)⋅(1)1.67×10−27
Calculating this gives:
ap=4.8×10−131.67×10−27≈2.874×1014m/s2
Final Results
- The acceleration of the neutron is 0m/s2.
- The acceleration of the proton is approximately 2.874×1014m/s2.
When charged particles move in a magnetic field, they experience a magnetic force given by the Lorentz force equation:
F=q(v×B)
where:
- F is the magnetic force,
- q is the charge of the particle,
- v is the velocity of the particle,
- B is the magnetic field.
The acceleration a of a particle can be calculated using Newton's second law:
a=Fm
Substituting the expression for the magnetic force into this equation gives:
a=q(v×B)m
- For the neutron:
- Charge qn=0 (neutrons are neutral).
- Mass mn≈1.67×10−27 kg.
- Charge qp=1.6×10−19 C.
- Mass mp≈1.67×10−27 kg.
Since the neutron has no charge:
an=qn⋅v⋅Bmn=0⋅(3×106)⋅11.67×10−27=0
Thus, the acceleration of the neutron is:
an=0m/s2
For the proton:
ap=qp⋅v⋅Bmp
Substituting the values:
ap=(1.6×10−19)⋅(3×106)⋅(1)1.67×10−27
ap=4.8×10−131.67×10−27≈2.874×1014m/s2
- The acceleration of the neutron is 0m/s2.
- The acceleration of the proton is approximately 2.874×1014m/s2.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:PRACTICE PROBLEMS
Explore 59 Videos
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:Conceptual Questions
Explore 29 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
- NUCLEIBook:MODERN PUBLICATIONChapter:NUCLEIExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 15 Videos
Similar Questions
A proton is projected with a velocity of 3X106ms−1 perpendicular to a uniform magnetic field of 0.6 T. find the acceleration of the proton.
View SolutionA proton is projected with a velocity of 3×106m/s perpendicular to a uniform magnetic field of 0.6T.Find the acceleration of the proton.mass of proton=53×10−27kg
View Solution
Knowledge Check
The radius of the path of an electron inoving at a speed of 3×107'm/s perpendicular to a magnetic field 5 x 10-4T is nearly
A15cmB45cmC27cmD34cmParticles 1, 2 and 3 are moving perpendicular to a uniform magnetic field, then particle
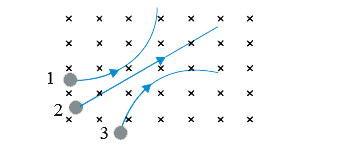 A1 is positively charged and particle 3 is negatively chargedB1 is negatively charged and particle 3 is positively chargedC1 is negatively charged and particle 2 is neutralD1 and 3 are positively charged and particle 2 is neutral
A1 is positively charged and particle 3 is negatively chargedB1 is negatively charged and particle 3 is positively chargedC1 is negatively charged and particle 2 is neutralD1 and 3 are positively charged and particle 2 is neutralIf a charged particle is a plane perpendicular to a uniform magnetic field with a time period T Then
AT2∝r3BT2∝rCT∝r2DT∝r0
A charged particle is projected at a very high speed perpendicular to a uniform magnetic field . The particle will
View SolutionWhat will be the path of a charged particle moving perpendicular to a uniform magnetic field?
View SolutionElectron, proton, He+ and Li+ are projected with the same speed perpendicular to a uniform magnetic field. Which particle will experience the maximum magnetic force?
View SolutionA proton and an alpha particle, both are moving with same initial velocity, perpendicular to uniform magnetic field of 1 T. Find the ratio of radii of circles described by the alpha particle and the proton.
View SolutionAssertion When a charged particle moves perpendicular to a uniform magnetic field then its momentum remains constant.
Reason Magnetic force acts perpendicular to the velocity of the particle.
View Solution