A non-conducting rod having circular cross section of radius R is suspended from a rigid support as shown in fig. A light and small coil of 300turns is wrapped tightly at the left end where uniform magnetic filed B exists in vertically downward direction. Air of density ρ hits the half of the right part of the rod with velocity V as shown in the fig. What should be current in clockwise direction (as seen from O) in the coil so that rod remains horizontal? Give answer in mA. Given 2Lv√πRBρ=1√5A−1/2.
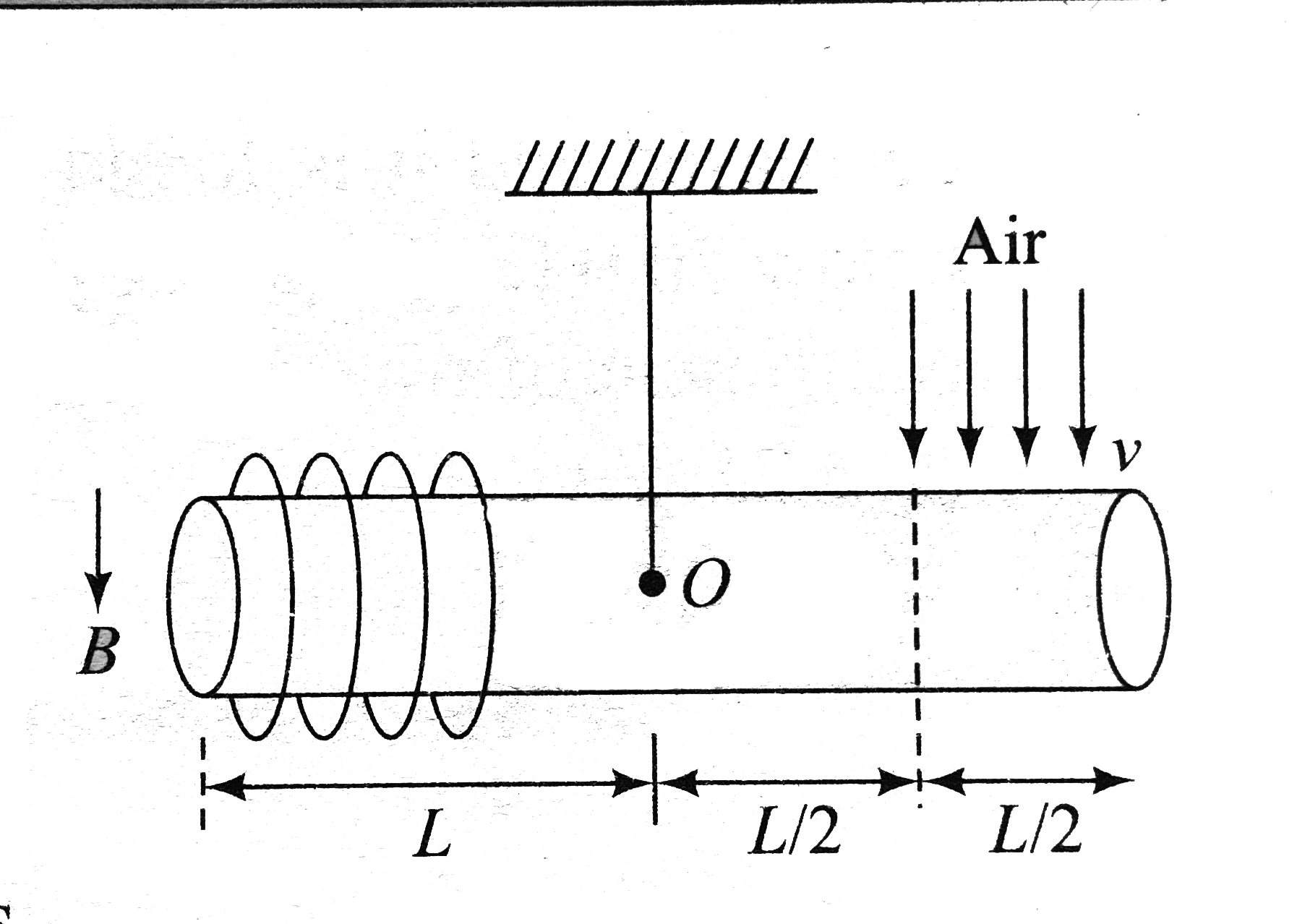
The correct Answer is:2
Force exerted by air on the rod =(ρ122R)v2=ρLRv2
Balancing torque about point O,NI(πR2)B=ρ=LRv23L4
⇒300πlBR=3ρv2L24
⇒I=ρL2v2400πBR=1100(Lv2√ρπBR)2=0.002A=2mA
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives Fill In The Blank
6 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives True /false
4 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Linked Comprehension
28 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View SolutionA small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __

View SolutionA rod of length L, cross sectional area A and density ρ is hanging from a rigid support by spring of stiffries k. A very small sphere of mass m is rigidly attached at the bottom of the rod. The rod is partially immersed in a liquid of density ρ. Find the period of small oscillations.
View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is

View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is

View SolutionA rod PQ is connected to the capacitor plates. The rod is placed in a magnetic field (B) directed downwards perpendicular to the plane of the paper. If the rod is pulled out of magnetic field with velocity →v as shown in Figure.
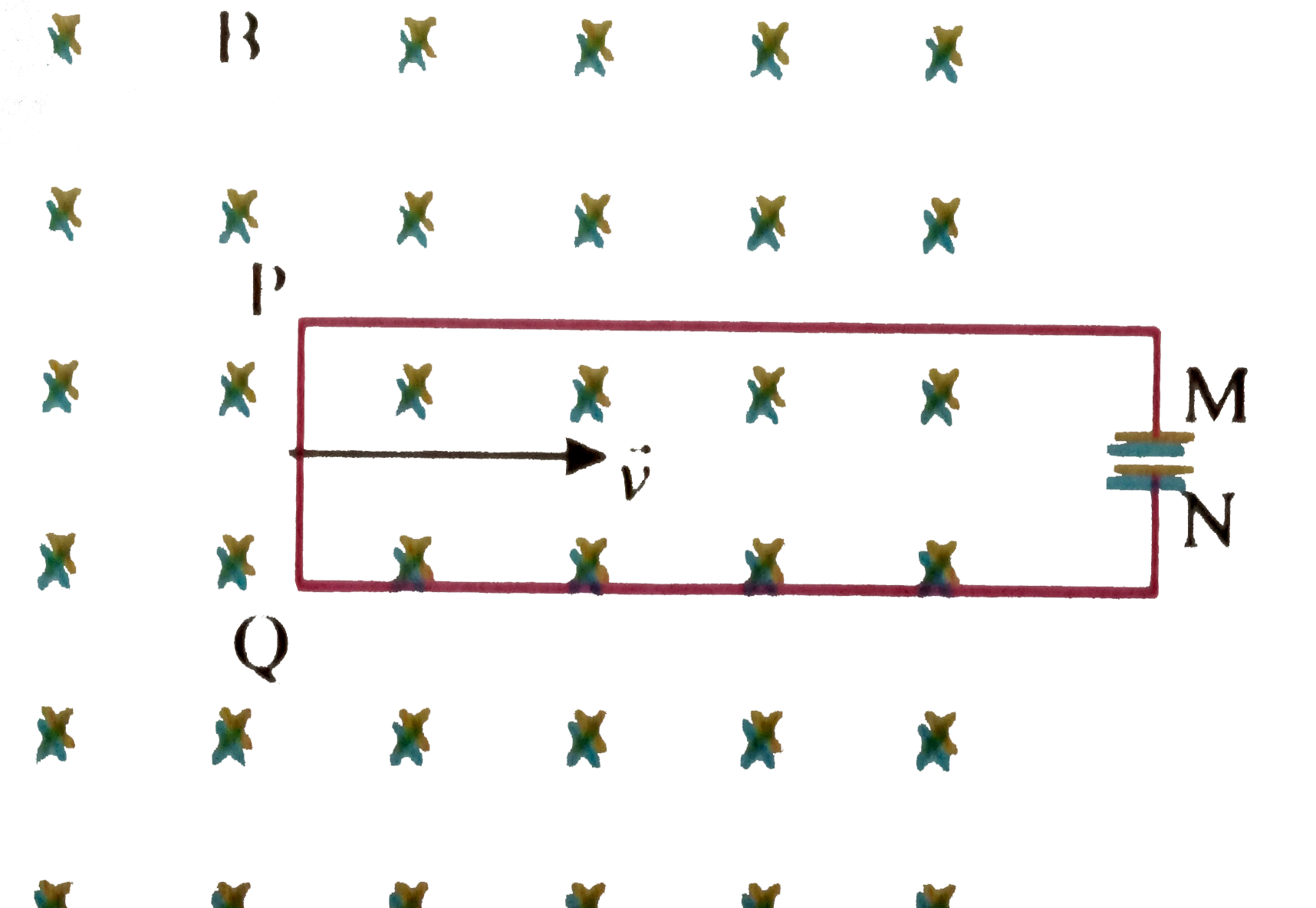
View SolutionA rod AB moves with a uniform velocity v in a uniform magnetic field as shown in figure

View SolutionA circular loop of radius a having n turns is kept in a horizontal plane. A uniform magnetic field B exists in a vertical direction as shown in Fig.313. Find the emf induced in the loop if the loop is roated with a uniform angualr velocity ω about
(a) an axis passing through the center and perendicular to the plane of the loop.
(b) the diameter.

View SolutionA circular coil of radius R is moving in a magnetic filed B with a velocity v as shown in the figure.

Find the emf across the diametrically opposite points A and B.
View SolutionA circular coil of radius R is moving in a magnetic filed B with a velocity v as shown in the figure.

Find the emf across the diametrically opposite points A and B.
View Solution
