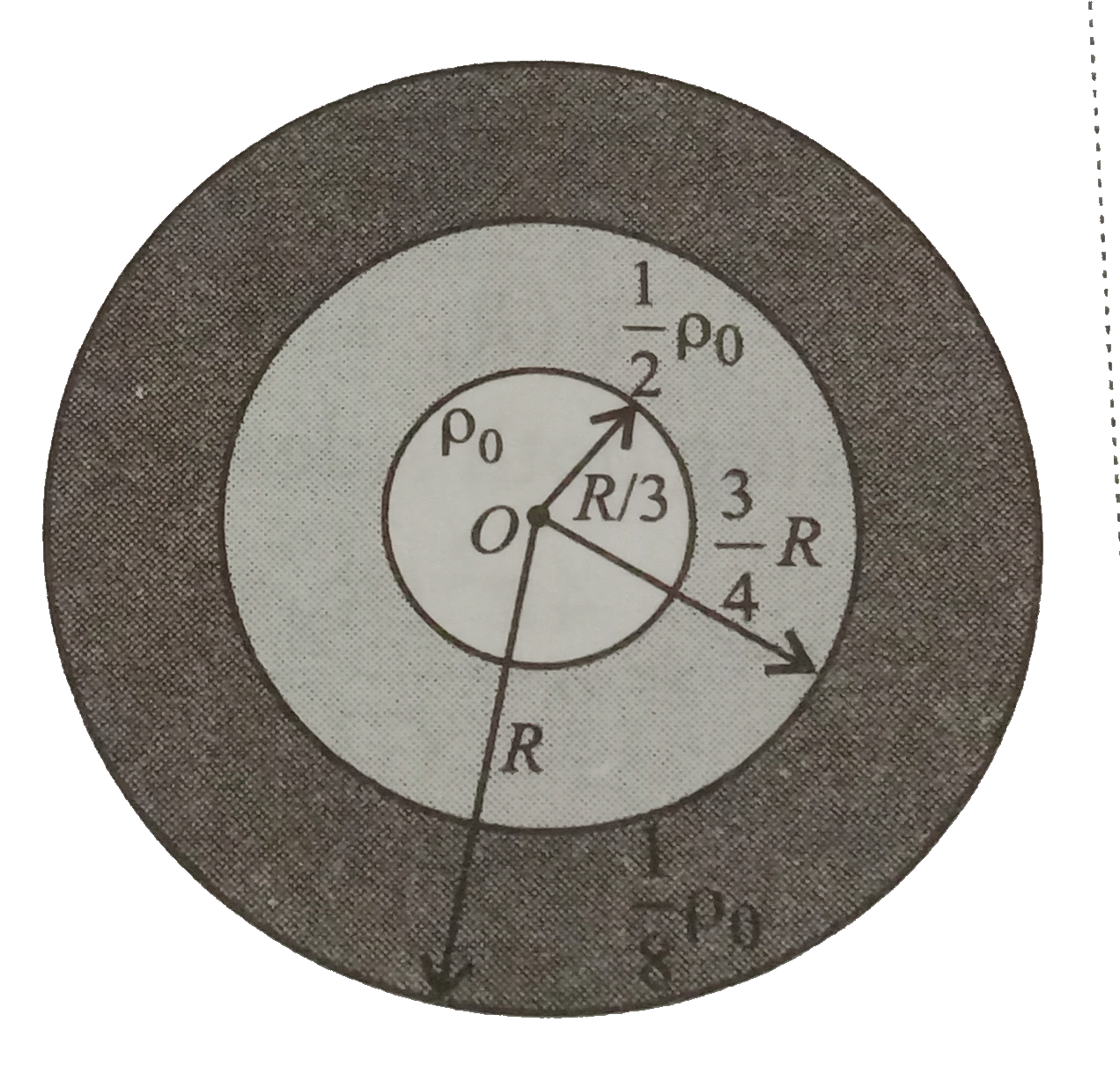
A non-homogeneous sphere of radius R has the following density variation :
$ρ {\begin{matrix} ρ_{0} & r \leq R / 3 \\ ρ_{0} / 2 & (R / 3) < r \leq (3 R / 4) \\ ρ_{0} / 8 & (3 R / 4) < r \leq R \end{matrix}$
The gravitational field at a distance 2R from the centre of the sphere is

A

$0.1 π G R ρ_{0}$

B

$0.2 π G R ρ_{0}$

C

$0.3 π G R ρ_{0}$

D

$0.4 π G R ρ_{0}$

Text Solution

Verified by Experts

The correct Answer is:A

(a) The gravitational field at a distance 2R from the centre of the sphere is
$E = \frac{G M}{{(2 R)}^{2}}$
where M is the mass of the whole sphere.

Here,
$M = \frac{4}{3} π {(\frac{R}{3})}^{3} ρ_{0} + {\frac{4}{3} π {(\frac{3}{4} R)}^{3} - \frac{4}{3} π {(\frac{R}{3})}^{3}} \frac{ρ_{0}}{2} + {\frac{4}{3} π R^{3} - \frac{4}{3} π {(\frac{3}{4} R)}^{3}} \frac{ρ_{0}}{8}$
$= \frac{4}{3} π R^{3} ρ_{0} {\frac{1}{27} + \frac{27}{128} - \frac{1}{54} + \frac{1}{8} - \frac{27}{512}}$
$= \frac{4}{3} π R^{3} ρ_{0} {\frac{512 + 2916 + 256 + 1728 - 729}{13824}}$
$= \frac{4}{3} π R^{3} ρ_{0} {\frac{5156 - 985}{13824}} = \frac{4}{3} π R^{3} ρ_{0} {\frac{4171}{13824}}$
$= 0.402 π R^{3} ρ_{0}$
$∴ E = \frac{G (0.402 π R^{3} ρ_{0})}{{(2 R)}^{2}} = 0.1 π G R ρ_{0}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A solid sphere of radius R has a volume charge density $ρ = ρ_{0} r^{2}$ (where $ρ_{0}$ is a constant ans r is the distance from centre). At a distance x from its centre (for $x < R$ ), the electric field is directly proportional to :
A $1 / x^{2}$
B $1 / x$
C $x^{3}$
D $x^{2}$
Question 2 - Select One
A spherical distribution of charge density $ρ = ρ_{0} (1 - r^{2} / 9)$ exists in the region $0 \leq r \leq 2$ . The dielectric constant of the medium is 2. Find the electric field inside the sphere at a distance r from the centre.
A $\frac{ρ_{0}}{90 ε_{0}} [15 r - r^{3}]$
B $\frac{ρ_{0}}{45 ε_{0}} [5 r - 8 r^{3}]$
C $\frac{ρ_{0}}{5 ε_{0}} [45 r - 2 r^{3}]$
D $\frac{ρ_{0}}{2 ε_{0}} [3 r - 4 r^{3}]$
Question 3 - Select One
A solid sphere of radius $R_{1}$ and volume charge density $ρ = \frac{ρ_{0}}{r}$ is enclosed by a hollow sphere of radius $R_{2}$ with negative surface charge density $σ$ , such that the total charge in the system is zero . $ρ_{0}$ is positive constant and $r$ is the distance from the centre of the sphere . The ratio $R_{2} / R_{1}$ is
A $\frac{σ}{ρ_{0}}$
B $\sqrt{\frac{2 σ}{ρ_{0}}}$
C $\sqrt{\frac{ρ_{0}}{2 σ}}$
D $\frac{ρ_{0}}{σ}$

NCERT FINGERTIPS-GRAVITATION-Miscellaneous Question

Home
Ask Doubt
Profile