A solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, ρ=ρ0rR, where ρ0 is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=πρ0R3 (ii) the electric field inside the sphere has a magnitude given by, E=KQr2R4
The correct Answer is:(a) →E=ρ0r24ε0ˆr;V=ρ0[4R3−r3]12ε0 (b) →E=ρ0R44ε0r2ˆr;V=ρ0R44ε0r
Step by step video & image solution for A solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, rho=rho_(0)r/R, where rho_(0) is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=pirho_(0)R^(3) (ii) the electric field inside the sphere has a magnitude given by, E=(KQr^(2))/R^(4) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Part - II
Explore 23 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
A conducting sphere of radius r has a charge . Then .
View SolutionA solid sphere of radius R has a charge Q distributed in its volume with a charge density ρ=kra, where k and a are constants and r is the distance from its centre. If the electric field at r=R2 is 18 times that r=R, find the value of a.
View Solution
Knowledge Check
A system consits of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density ρ=αr, where α is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
Aα2ε0B2αε0C2παR2DNone of these
An insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
View SolutionA non-conducting solid sphere of radius R, has a uniform charge density. The graph representing variation of magnitude of electric field (E) as a function of distance (x) from the centre of the sphere is
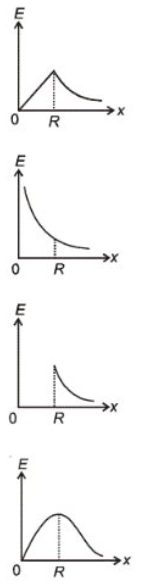
View SolutionA solid insulating sphere of radius R has a nonuniform charge density that varies with r according to the expression ρ=Ar2, where A is a constant and r<R is measured from the centre of the sphere. Show that (a) the magnitude of the electric field outside (r>R) the sphere is E=AR5/5ε0r2 and (b) the magnitude of the electric field inside (r<R) the sphere is E=Ar3/5ε0.

View SolutionA non-conducting solid sphere has volume charge density that varies as ρ=ρ0 r, where ρ0 is a constant and r is distance from centre. Find out electric field intensities at following positions.
(i) r<R (ii) r≥R
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
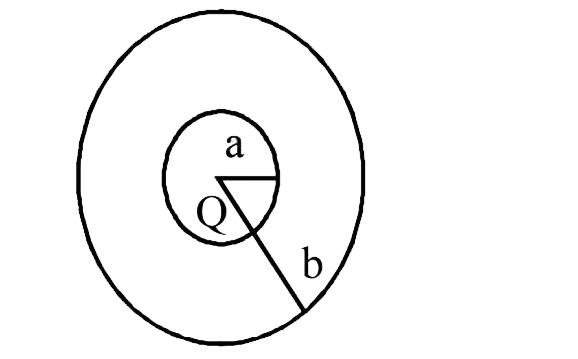
View SolutionThe region between two concentric spheres of radii ‘a’ and ‘b’, respectively (see figure), has volume charge density p=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is :
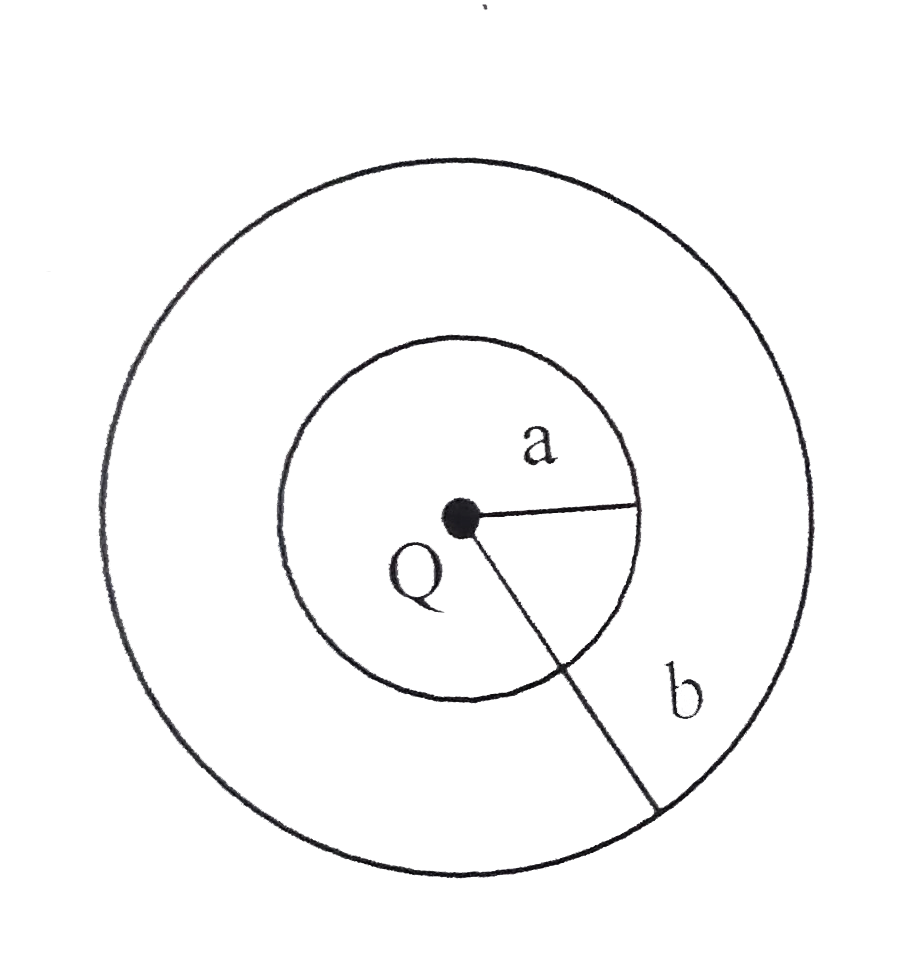
View SolutionPotential at a point x-distance from the centre inside the conducting sphere of radius R and charged with charge Q is
View Solution