A solid sphere of radius R1 and volume charge density ρ=ρ0r is enclosed by a hollow sphere of radius R2 with negative surface charge density σ, such that the total charge in the system is zero . ρ0 is positive constant and r is the distance from the centre of the sphere . The ratio R2/R1 is
σρ0
√2σρ0
√ρ02σ
ρ0σ
The correct Answer is:C
To solve the problem, we need to find the ratio R2R1 given a solid sphere of radius R1 with a volume charge density ρ=ρ0r and a hollow sphere of radius R2 with a negative surface charge density σ such that the total charge in the system is zero.
1. Identify the Charge of the Solid Sphere Q1:
- The charge Q1 in the solid sphere can be calculated by integrating the volume charge density over the volume of the sphere.
- The volume charge density is given as ρ=ρ0r.
- The charge element dQ for a thin spherical shell of radius r and thickness dr is:
dQ=ρ⋅dV=ρ⋅(4πr2dr)=ρ0r⋅(4πr2dr)=4πρ0rdr
- To find the total charge Q1, integrate from 0 to R1:
Q1=∫R104πρ0rdr=4πρ0∫R10rdr=4πρ0(r22)R10=4πρ0R212=2πρ0R21
2. Identify the Charge of the Hollow Sphere Q2:
- The charge Q2 on the hollow sphere is given by the surface charge density σ:
Q2=−σ⋅A=−σ⋅(4πR22)=−4πσR22
3. Set Up the Equation for Total Charge:
- Since the total charge in the system is zero:
Q1+Q2=0
- Substituting the expressions for Q1 and Q2:
2πρ0R21−4πσR22=0
4. Rearranging the Equation:
- Rearranging gives:
2πρ0R21=4πσR22
- Dividing both sides by 2π:
ρ0R21=2σR22
5. Finding the Ratio R2R1:
- Rearranging the equation for R2:
R22R21=ρ02σ
- Taking the square root gives:
R2R1=√ρ02σ
Final Answer:
The ratio R2R1 is:
R2R1=√ρ02σ
- The charge Q1 in the solid sphere can be calculated by integrating the volume charge density over the volume of the sphere.
- The volume charge density is given as ρ=ρ0r.
- The charge element dQ for a thin spherical shell of radius r and thickness dr is:
dQ=ρ⋅dV=ρ⋅(4πr2dr)=ρ0r⋅(4πr2dr)=4πρ0rdr
- To find the total charge Q1, integrate from 0 to R1:
Q1=∫R104πρ0rdr=4πρ0∫R10rdr=4πρ0(r22)R10=4πρ0R212=2πρ0R21
- The charge Q2 on the hollow sphere is given by the surface charge density σ:
Q2=−σ⋅A=−σ⋅(4πR22)=−4πσR22
- Since the total charge in the system is zero:
Q1+Q2=0
- Substituting the expressions for Q1 and Q2:
2πρ0R21−4πσR22=0
- Rearranging gives:
2πρ0R21=4πσR22
- Dividing both sides by 2π:
ρ0R21=2σR22
- Rearranging the equation for R2:
R22R21=ρ02σ
- Taking the square root gives:
R2R1=√ρ02σ
The ratio R2R1 is:
R2R1=√ρ02σ
Similar Questions
Two charged spheres of radii R1andR2 having equal surface charge density. The ratio of their potential is
View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
View SolutionThe magnitude of the electric field on the surface of a sphere of radius r having a uniform surface charge density σ is
View SolutionA solid sphere of radius R has a charge Q distributed in its volume with a charge density ρ=kra, where k and a are constants and r is the distance from its centre. If the electric field at r=R2 is 18 times that r=R, find the value of a.
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be
 View Solution
View SolutionA solid ball of radius R has a charge density ρ given by ρ=ρ0(1−rR)for0≤r≤R The electric field outside the ball is :
View SolutionA solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
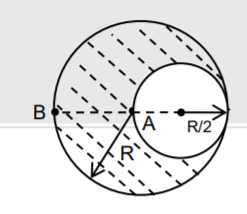 View Solution
View SolutionA sphere of radius R has a variable charge density ρ(r)=ρ0rn−1(r≤R). If ratio of "potential at centre" and "potential at surface" be 3/2 then find the value of n
View SolutionIf the potential at the centre of a uniformly charged hollow sphere of radius R is V, then electric field at a distance r from the centre of sphere will be (r>R).
 View Solution
View SolutionA hollow conducting sphere of radius R has a charge (+Q) on its surface. What is the electric potential within the
sphere at a distance r=R3 from its centre ?View Solution

