A non-uniform rod AB has a mass M ad length 2l. The mass per unit length of the rod is mx at a point of the rod distant x from A. find the moment of inertia of this rod about an axis perpendicular to the rod (a) through A (b) through the mid-point of AB.
To find the moment of inertia of a non-uniform rod AB with mass M and length 2l about two different axes, we will follow these steps:
Part (a): Moment of Inertia about an Axis through A
1. Define the mass per unit length: The mass per unit length of the rod is given as mx, where m is a constant and x is the distance from point A.
2. Express the mass element: The mass of a small element dx at a distance x from A can be expressed as:
dm=mxdx
3. Moment of inertia of the small element: The moment of inertia dI of this small element about the axis through A is given by:
dI=x2dm=x2⋅(mxdx)=mx3dx
4. Integrate to find total moment of inertia: To find the total moment of inertia I of the rod from x=0 to x=2l:
I=∫2l0mx3dx
5. Calculate the integral:
I=m∫2l0x3dx=m(x44)2l0=m⋅(2l)44=m⋅16l44=4ml4
6. Find the value of m: The total mass M of the rod can be expressed as:
M=∫2l0mxdx=m(x22)2l0=m⋅(2l)22=2ml2
Thus, m=M2l2.
7. Substitute m back into the moment of inertia:
I=4(M2l2)l4=4Ml42l2=2Ml2
Part (b): Moment of Inertia about an Axis through the Midpoint of AB
1. Define the new axis: The midpoint of the rod is at x=0 (with A at −l and B at l).
2. Express the mass element: The mass of a small element dx at a distance x from the midpoint can be expressed as:
dm=m(l−x)dx
3. Moment of inertia of the small element: The moment of inertia dI of this small element about the axis through the midpoint is given by:
dI=(l−x)2dm=(l−x)2⋅(m(l−x)dx)=m(l−x)3dx
4. Integrate to find total moment of inertia: To find the total moment of inertia I of the rod from x=−l to x=l:
I=∫l−lm(l−x)3dx
5. Calculate the integral:
I=m∫l−l(l−x)3dx
This integral can be simplified by symmetry or evaluated directly.
6. Using symmetry: The integral can be evaluated as:
I=m((l−x)44)l−l=m((l+l)44−0)=m⋅(2l)44=m⋅16l44=4ml4
7. Substituting m: Using m=M2l2:
I=4(M2l2)l4=4Ml42l2=2Ml2
Final Results:
- Moment of Inertia about A: IA=2Ml2
- Moment of Inertia about the midpoint: Imid=Ml23
dm=mxdx
dI=x2dm=x2⋅(mxdx)=mx3dx
I=∫2l0mx3dx
I=m∫2l0x3dx=m(x44)2l0=m⋅(2l)44=m⋅16l44=4ml4
M=∫2l0mxdx=m(x22)2l0=m⋅(2l)22=2ml2
Thus, m=M2l2.
I=4(M2l2)l4=4Ml42l2=2Ml2
dm=m(l−x)dx
dI=(l−x)2dm=(l−x)2⋅(m(l−x)dx)=m(l−x)3dx
I=∫l−lm(l−x)3dx
I=m∫l−l(l−x)3dx
This integral can be simplified by symmetry or evaluated directly.
I=m((l−x)44)l−l=m((l+l)44−0)=m⋅(2l)44=m⋅16l44=4ml4
I=4(M2l2)l4=4Ml42l2=2Ml2
- Moment of Inertia about A: IA=2Ml2
- Moment of Inertia about the midpoint: Imid=Ml23
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.2
4 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.3
4 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example
1 Video
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionA rod of length L is composed of a uniform length 1/2 L of wood mass is mw and a uniform length 1/2 L of brass whose mass is mb. The moment of inertia I of the rod about an axis perpendicular to the rod and through its centre is equal to
View SolutionA thin rod of length L of mass M is bent at the middle point O at an angle of 60∘. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
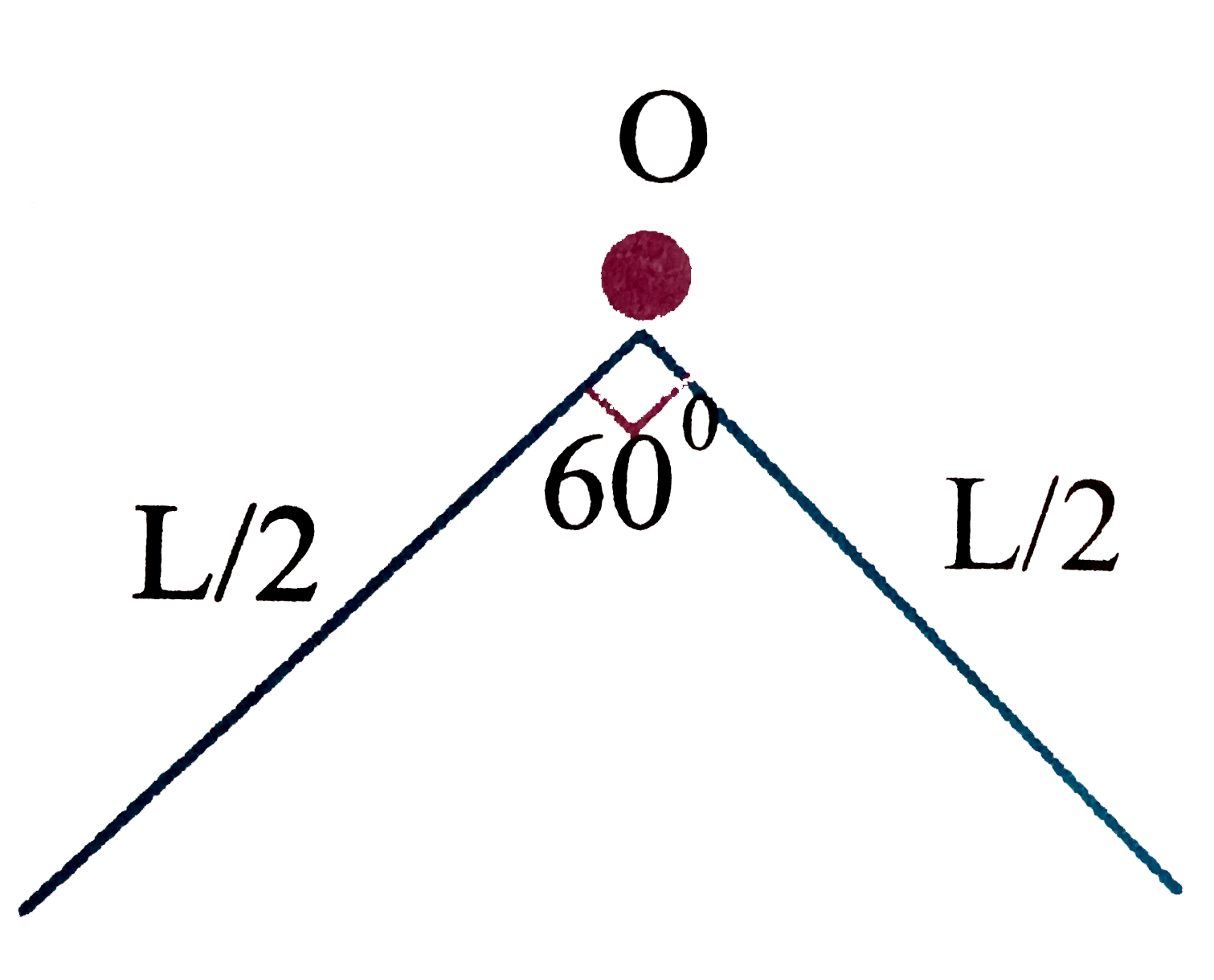
View SolutionA thin rod of length 4l, mass 4 m is bent at the point as shown in the figure. What is the moment of inertia of the rod about the axis passing through O and perpendicular to the plane of the paper?

View Solution
A thin rod of length 4l, mass 4 m is bent at the point as shown in the figure. What is the moment of inertia of the rod about the axis passing through O and perpendicular to the plane of the paper?
View Solution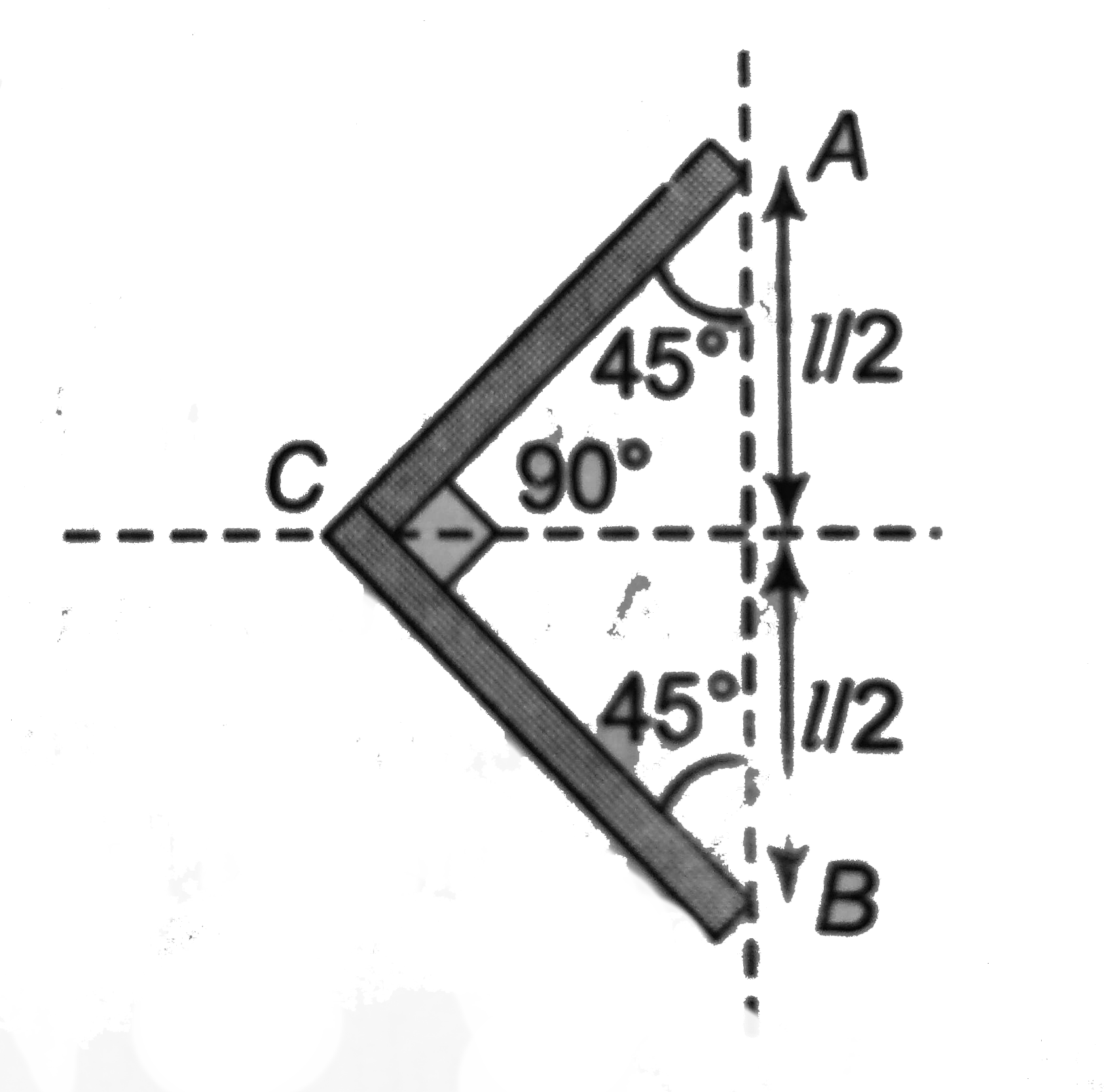
Linear mass density of the two rods system, AC and CD is x. moment of inertia of two rods about an axis passing through AB is
View SolutionCalculate the moment of inertia of a rod of mass 2 kg and length 5 m about an axis perpendicular to it and passing through one of its ends.
View SolutionTwo uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.

View Solution
