A number of spherical conductors of different radius have same potential. Then the surface charge density on them.
is proportional to their radii
is inversely proportional to their radii
are equal
is proportional to square of their radii
The correct Answer is:B
To solve the problem of determining the surface charge density on spherical conductors of different radii that have the same potential, we can follow these steps:
1. Understanding the Concept of Electric Potential:
- For a spherical conductor, the electric potential V at its surface is given by the formula:
V=kQR
where k is Coulomb's constant, Q is the charge on the sphere, and R is the radius of the sphere.
2. Setting Up the Equation for Different Spheres:
- Let’s consider two spherical conductors with charges Q1 and Q2, and radii R1 and R2 respectively. Since they have the same potential:
V1=V2
This implies:
kQ1R1=kQ2R2
3. Simplifying the Equation:
- We can cancel k from both sides:
Q1R1=Q2R2
- Rearranging gives us:
Q1=Q2⋅R1R2
4. Finding Surface Charge Density:
- The surface charge density σ is defined as charge per unit area. For a sphere, the surface area A is given by:
A=4πR2
- Thus, the surface charge density for each sphere can be expressed as:
σ1=Q14πR21andσ2=Q24πR22
5. Substituting for Charge:
- Using the relationship established earlier, we can substitute for Q1:
σ1=Q2⋅R1R24πR21
- This simplifies to:
σ1=Q24πR22⋅1R1
- Similarly, for σ2:
σ2=Q24πR22
6. Establishing the Relationship:
- From the above equations, we can see that:
σ1=σ2R1/R2
- This indicates that the surface charge density σ is inversely proportional to the radius R:
σ∝1R
Conclusion:
Thus, we conclude that the surface charge density on the spherical conductors is inversely proportional to their radii.
- For a spherical conductor, the electric potential V at its surface is given by the formula:
V=kQR
where k is Coulomb's constant, Q is the charge on the sphere, and R is the radius of the sphere.
- Let’s consider two spherical conductors with charges Q1 and Q2, and radii R1 and R2 respectively. Since they have the same potential:
V1=V2
This implies:
kQ1R1=kQ2R2
- We can cancel k from both sides:
Q1R1=Q2R2
- Rearranging gives us:
Q1=Q2⋅R1R2
- The surface charge density σ is defined as charge per unit area. For a sphere, the surface area A is given by:
A=4πR2
- Thus, the surface charge density for each sphere can be expressed as:
σ1=Q14πR21andσ2=Q24πR22
- Using the relationship established earlier, we can substitute for Q1:
σ1=Q2⋅R1R24πR21
- This simplifies to:
σ1=Q24πR22⋅1R1
- Similarly, for σ2:
σ2=Q24πR22
- From the above equations, we can see that:
σ1=σ2R1/R2
- This indicates that the surface charge density σ is inversely proportional to the radius R:
σ∝1R
Thus, we conclude that the surface charge density on the spherical conductors is inversely proportional to their radii.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced44videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Comprehension36videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery21videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
Similar Questions
A number of spherical conductors of different radii are charged to same potential. The surface charge density of each conductor is related with its radius as
View SolutionAssertion: The surface charge densities of two spherical conductors of different radii are equal. Then the electric field intensities near their surface are also equal.
Reason: Surface charge density is equal to charge per unit area.View Solution(A ): The surface densities of two spherical conductors of different radii are equal. Then the electric field intensities near their surface are also equal.
(R ): Surface density is equal to charge per unit area.View SolutionA hollow spherical conductor of radius r potential of 100 V at its outer surface. The potential inside the hollow at a distance ofr2 from its centre is
View SolutionTwo spheres A and B of radius 'a' and 'b' respectively are at same electric potential. The ratio of the surface charge densities of A and B is
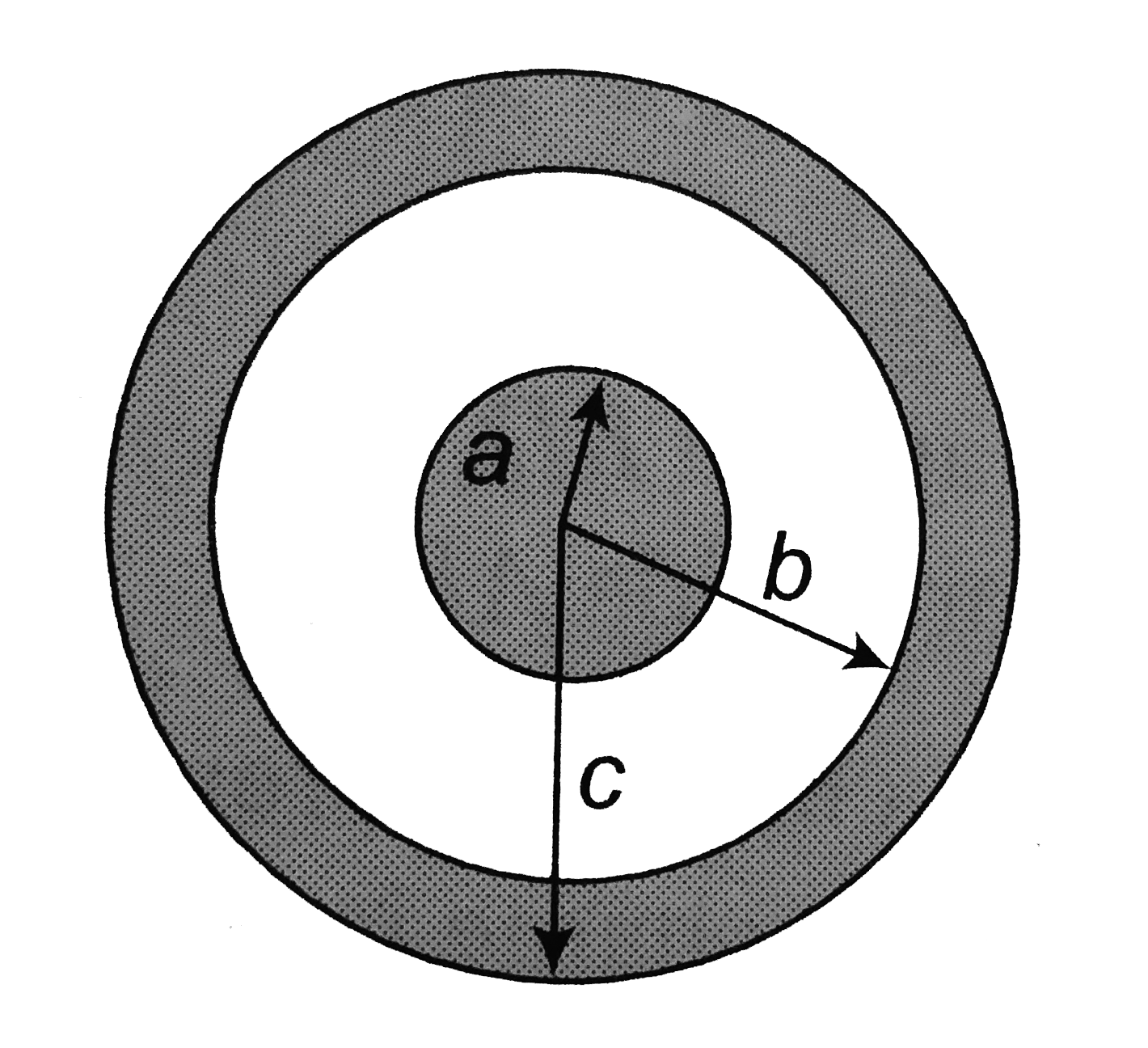
View SolutionA solid conducting sphere of radius a has a net positive charge 2Q. A conducting spherical shell of inner radius b and outer radius c is concentric with the solid sphere and has a net charge −Q. The surface charge density on the inner and outer surfaces of the spherical shell will be
 View Solution
View SolutionA spherical conductor of radius 2 m is charged to a potential of 120 V. It is now placed inside another hollow spherical conductor of radius 6 m. calculate the potential of bigger sphere, if the smaller sphere is made to touch the bigger sphere
View SolutionThe electric field inside a spherical shell of uniform surface charge density is
View SolutionA solid spherical conductor of radius R has a spherical cavity of radius at its centre. A charge is kept at the centre. The charge at the inner surface, outer surface are respectively.
View SolutionA spherical conductor of radius 2m is charged to a potential of 120V. It is now placed inside another hollow spherical conductor of radius 6m. Calculate the potential to which the bigger sphere would be raised
View Solution

