A number of spherical conductors of different radii are charged to same potential. The surface charge density of each conductor is related with its radius as
σ∝1R2
σ∝1R
σ∝R
none of these
The correct Answer is:B
To solve the problem of finding the relationship between the surface charge density of spherical conductors charged to the same potential and their radii, we can follow these steps:
1. Understanding the Problem: We have spherical conductors of different radii (let's denote them as r1,r2,…) that are charged to the same electric potential.
2. Potential of a Sphere: The electric potential V of a charged sphere is given by the formula:
V=k⋅QR
where k is Coulomb's constant, Q is the charge on the sphere, and R is the radius of the sphere.
3. Setting Up the Equations: For two spheres with radii r1 and r2 and charges q1 and q2, since they are at the same potential:
V1=V2
This gives us:
k⋅q1r1=k⋅q2r2
4. Simplifying the Equation: We can cancel k from both sides:
q1r1=q2r2
Rearranging gives:
q1q2=r1r2
This implies that the charge Q is directly proportional to the radius R:
q∝r
5. Surface Charge Density: The surface charge density σ is defined as:
σ=QA
where A is the surface area of the sphere. The surface area A of a sphere is given by:
A=4πR2
Therefore, we can express the surface charge density as:
σ=Q4πR2
6. Substituting for Charge: Since we established that Q∝R, we can write Q=kR for some constant k. Substituting this into the equation for σ:
σ=kR4πR2
7. Simplifying the Expression: This simplifies to:
σ=k4πR
Thus, we find that:
σ∝1R
Conclusion:
The surface charge density σ is inversely proportional to the radius R of the spherical conductor.
V=k⋅QR
where k is Coulomb's constant, Q is the charge on the sphere, and R is the radius of the sphere.
V1=V2
This gives us:
k⋅q1r1=k⋅q2r2
q1r1=q2r2
Rearranging gives:
q1q2=r1r2
This implies that the charge Q is directly proportional to the radius R:
q∝r
σ=QA
where A is the surface area of the sphere. The surface area A of a sphere is given by:
A=4πR2
Therefore, we can express the surface charge density as:
σ=Q4πR2
σ=kR4πR2
σ=k4πR
Thus, we find that:
σ∝1R
The surface charge density σ is inversely proportional to the radius R of the spherical conductor.
Similar Questions
A number of spherical conductors of different radius have same potential. Then the surface charge density on them.
View Solution(A ): The surface densities of two spherical conductors of different radii are equal. Then the electric field intensities near their surface are also equal.
(R ): Surface density is equal to charge per unit area.
View SolutionA spherical conductor is placed near another positively charged conductor. The net charge acquired by spherical conductor will be
View Solution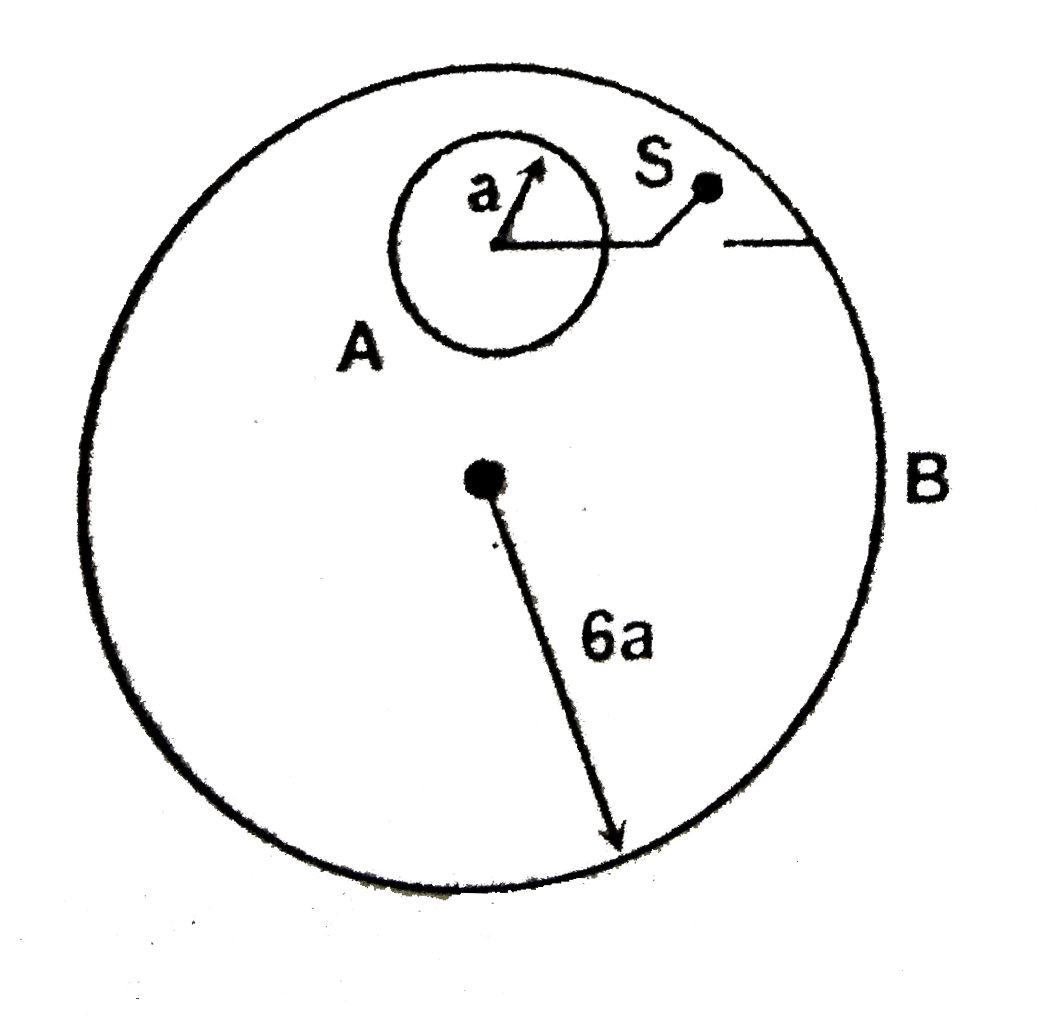
A small spherical conductor 'A' of radias 'a' is initially charged to a potential 'V' and then placed inside an uncharged spherical conducting shell 'B' of radius 6a as shown. The potential of the spherical conductor 'A' after closing the switch S is
View SolutionAssertion: The surface charge densities of two spherical conductors of different radii are equal. Then the electric field intensities near their surface are also equal.
Reason: Surface charge density is equal to charge per unit area.
View SolutionWhen we charge a conductor, we are raising or lowering its potential.
View SolutionTwo spheres of radii 2 cm and 3 cm are charged to the same potential. If σ and σ2 be respectively the values of surface charge density on the conductors, then the ratio σ1σ2 will be
View SolutionA spherical conductor of radius 2m is charged to a potential of 120V. It is now placed inside another hollow spherical conductor of radius 6m. Calculate the potential to which the bigger sphere would be raised
View SolutionAcross the surface of a charged conductor, the electric
View SolutionA spherical conductor of radius 2 m is charged to a potential of 120 V. It is now placed inside another hollow spherical conductor of radius 6 m. calculate the potential of bigger sphere, if the smaller sphere is made to touch the bigger sphere
View Solution
