A spherical conductor of radius 2 m is charged to a potential of 120 V. It is now placed inside another hollow spherical conductor of radius 6 m. calculate the potential of bigger sphere, if the smaller sphere is made to touch the bigger sphere
120 V
60 V
80 V
40 V
The correct Answer is:D
To solve the problem, we need to follow these steps:
Step 1: Calculate the charge on the smaller sphere
The potential V of a spherical conductor is given by the formula:
V=kQR
where:
- V is the potential,
- k is the electrostatic constant (which we can ignore for this calculation since we are looking for a relationship),
- Q is the charge,
- R is the radius of the sphere.
Given:
- The potential V=120V
- The radius of the smaller sphere R1=2m
Rearranging the formula to find kQ:
kQ=V⋅R1=120V⋅2m=240V \cdot m
Step 2: Understand the effect of touching the bigger sphere
When the smaller sphere (charged to 120 V) touches the bigger sphere, the charge will redistribute between the two spheres. Since they are conductors, they will reach the same potential after contact.
Step 3: Calculate the potential of the bigger sphere after contact
After the smaller sphere touches the bigger sphere, we need to find the new potential of the bigger sphere. The radius of the bigger sphere is R2=6m.
The potential V′ of the bigger sphere after contact can be calculated using the formula:
V′=kQR2
Substituting kQ=240V \cdot m and R2=6m:
V′=240V \cdot m6m=40V
Conclusion
The potential of the bigger sphere after the smaller sphere touches it is 40V.
The potential V of a spherical conductor is given by the formula:
V=kQR
where:
- V is the potential,
- k is the electrostatic constant (which we can ignore for this calculation since we are looking for a relationship),
- Q is the charge,
- R is the radius of the sphere.
- The potential V=120V
- The radius of the smaller sphere R1=2m
kQ=V⋅R1=120V⋅2m=240V \cdot m
When the smaller sphere (charged to 120 V) touches the bigger sphere, the charge will redistribute between the two spheres. Since they are conductors, they will reach the same potential after contact.
After the smaller sphere touches the bigger sphere, we need to find the new potential of the bigger sphere. The radius of the bigger sphere is R2=6m.
V′=kQR2
Substituting kQ=240V \cdot m and R2=6m:
V′=240V \cdot m6m=40V
The potential of the bigger sphere after the smaller sphere touches it is 40V.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
A spherical conductor of radius 2m is charged to a potential of 120V. It is now placed inside another hollow spherical conductor of radius 6m. Calculate the potential to which the bigger sphere would be raised
View Solution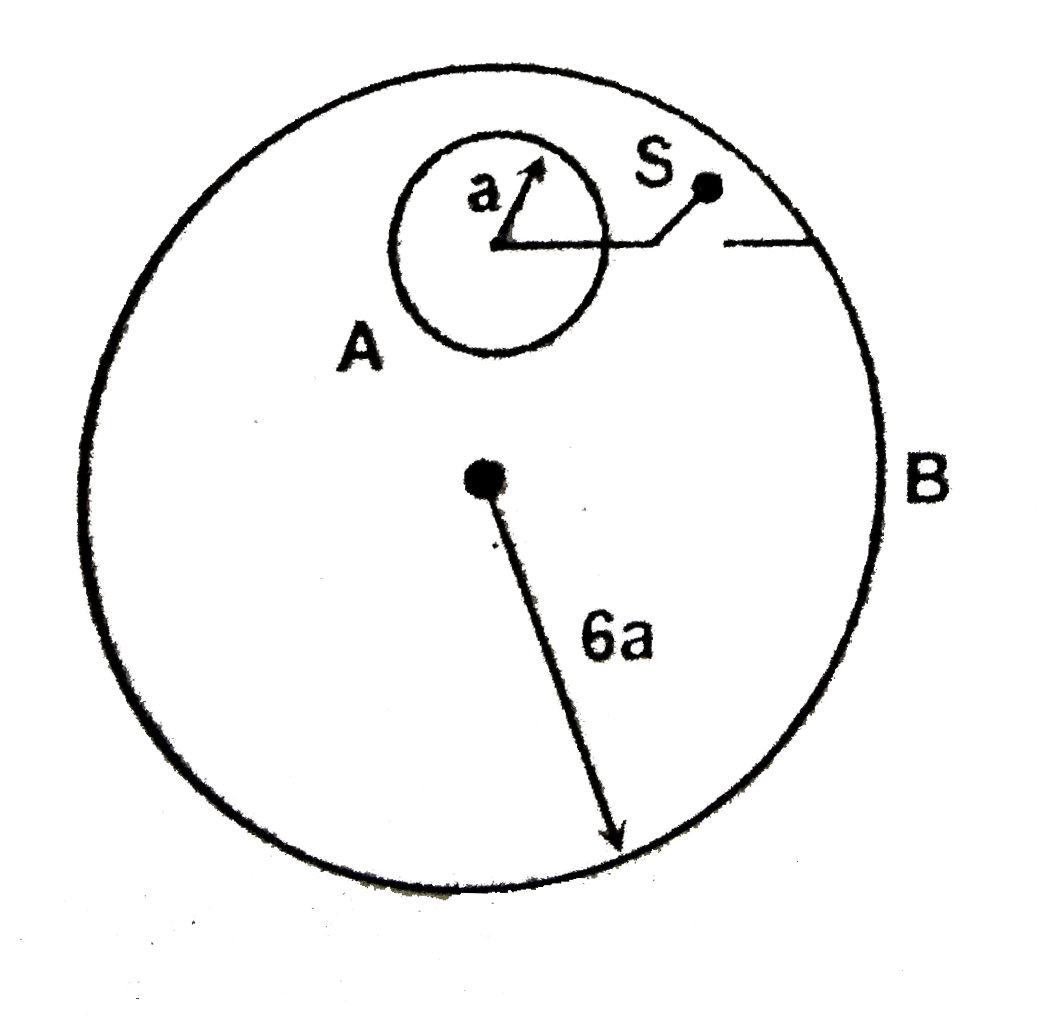
A small spherical conductor 'A' of radias 'a' is initially charged to a potential 'V' and then placed inside an uncharged spherical conducting shell 'B' of radius 6a as shown. The potential of the spherical conductor 'A' after closing the switch S is
View Solution
Knowledge Check
Metallic sphere of radius R is charged to potential V. Then charge q is proportional to
AVBRCboth V and RDnone of these
A hollow metallic sphere of radius 0.1 m is charged to a potential of 5 V. The potential at its centre is
View SolutionCapacitance (in F) of a spherical conductor with radius 1m is
View SolutionA hollow spherical conductor of radius r potential of 100 V at its outer surface. The potential inside the hollow at a distance ofr2 from its centre is
View SolutionA number of spherical conductors of different radius have same potential. Then the surface charge density on them.
View SolutionA small sphere is charged to a potential of 50 V and a big hollow sphere is charged to a potential of 100 V. Electricity will flow from the smaller sphere to the bigger one when
View SolutionA hollow metal sphere of radius 6 cm is charged such that the potential on its surface is 12 V.What is the potential at the centre of the sphere?
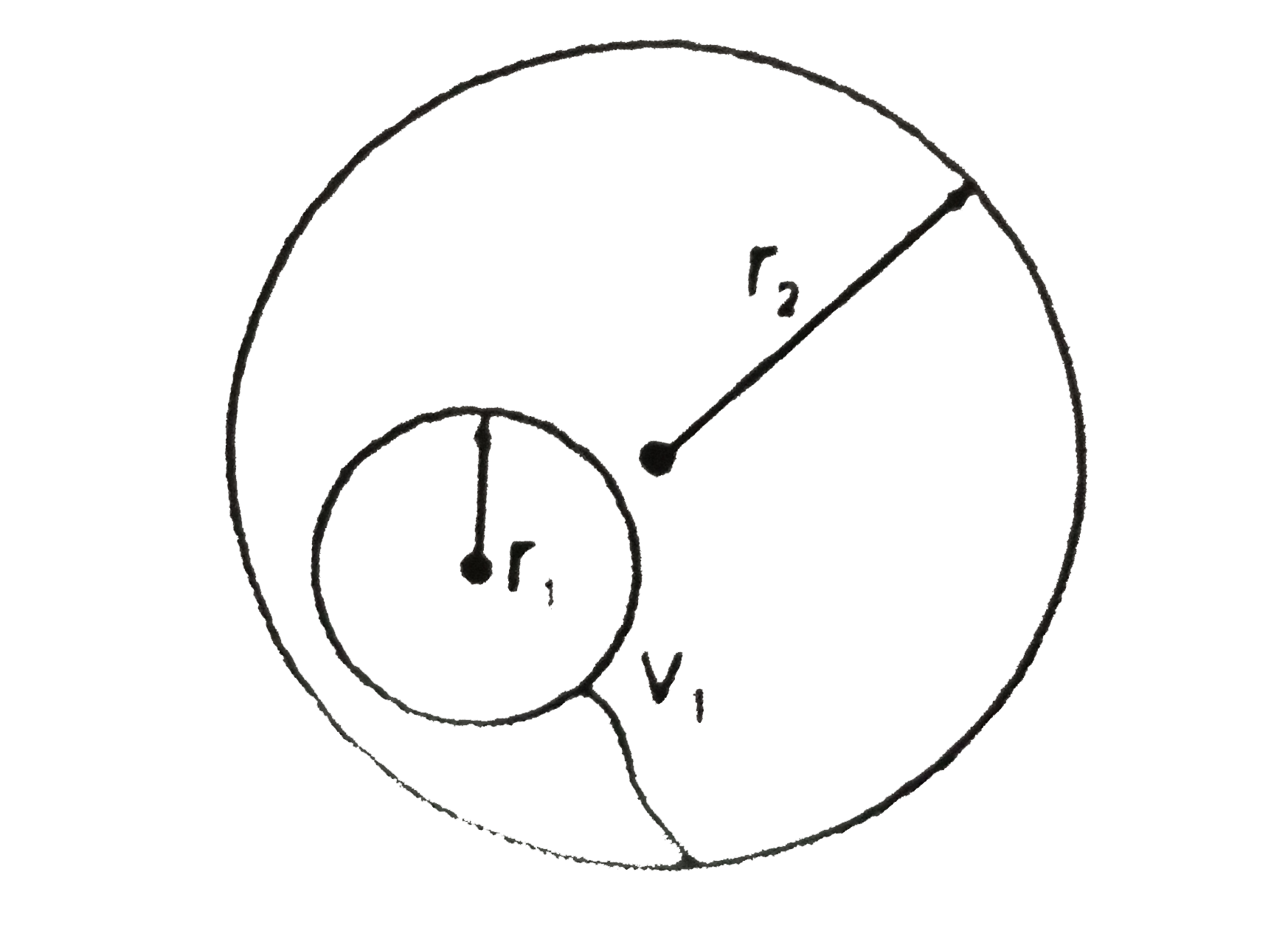
View SolutionA metal sphere of radius r1 charges to a potential V1 is then placed in a thin-walled uncharged conducting spherical shell of radius r2. Determine the potential acquired by the spherical shell after it has been connected for a short time to the sphere by a conductor.
View Solution
