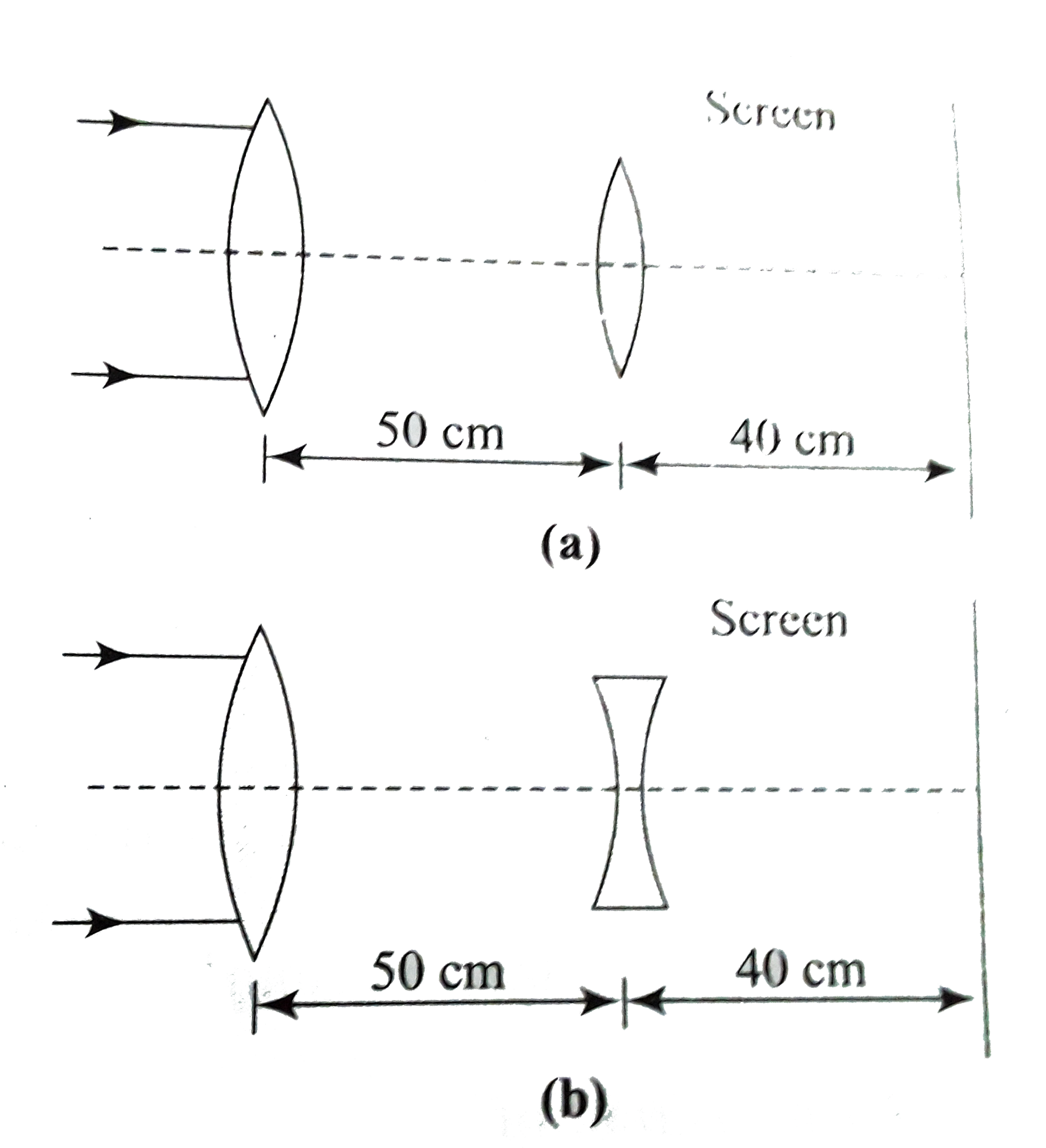
A parallel beam of light falls successively on a thin convex lens of focal length 40 cm and then ono a thini convex lens of focal length 10cm as shown in figure.
In figure, the second lens is an equiconcave lens of focal length 10cm and made of a material of refractive index 1.5. In both the cases, the second lens has an aperture equal to 1cm.
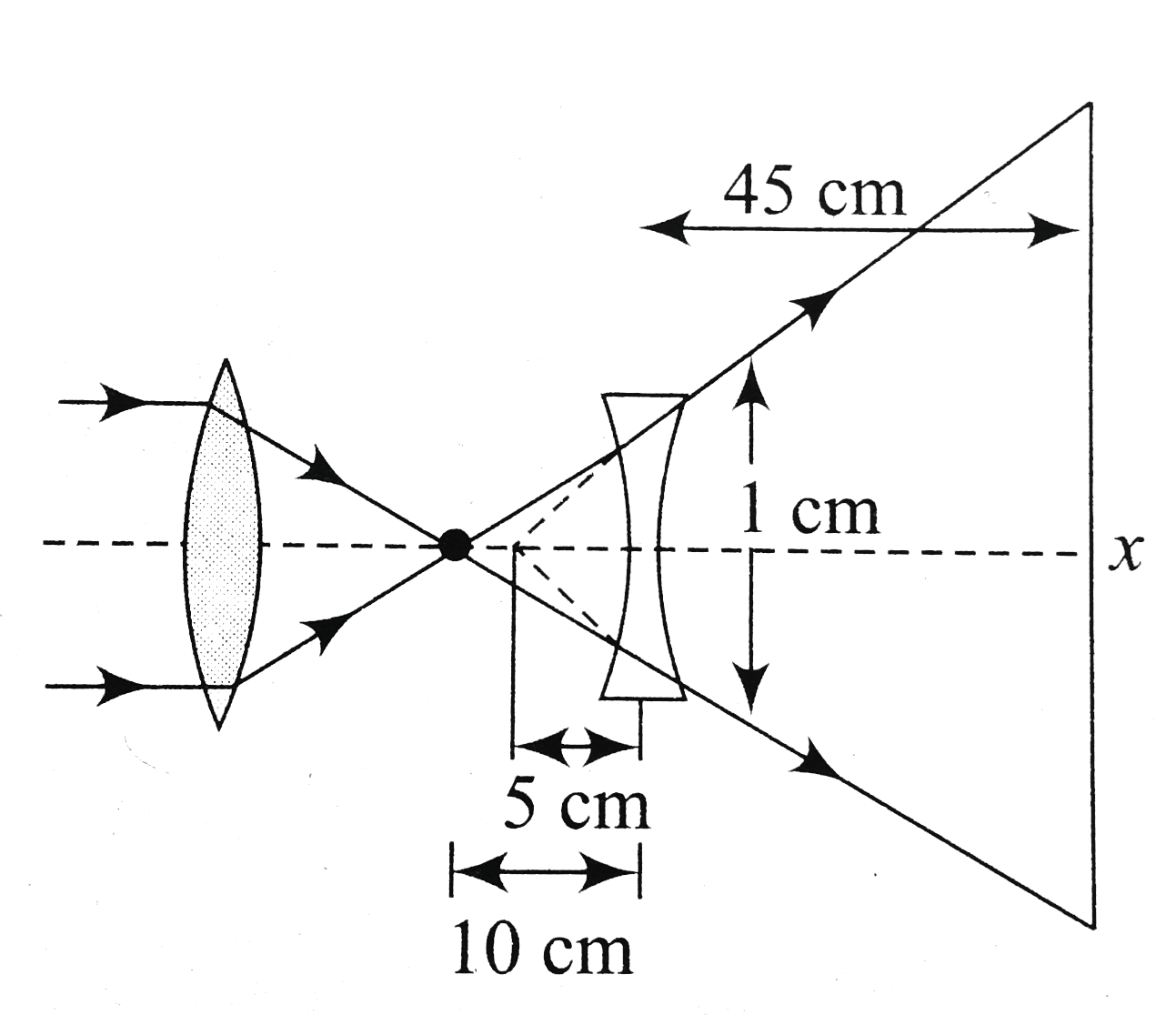
Q. Now, a liquid of refractive index is filled to the right of the second lens in case B such that the area illuminated in both the cases is the same. Determing the refractive index of the liquid.
1
2.5
3
1.5
The correct Answer is:c.
In case (a), the incident parallel beam emerges as a parallel beam. So area illuminated,
In case (b), let x be the diameter of the area illuminated.
Then,
When liquid of refractive index is filled to the right of this lens, the first surface of the lens (radius of curvature forms the imag at the object only. Considering the refraction at the second surface.
(therefore, same area
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer15videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Archives7videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
A parallel beam of light falls successively on a thin convex lens of focal length 40 cm and then ono a thin convex lens of focal length 10cm as shown in figure.
In figure, the second lens is an equi-concave lens of focal length 10cm and made of a material of refractive index 1.5. In both the cases, the second lens has an aperture equal to 1cm.
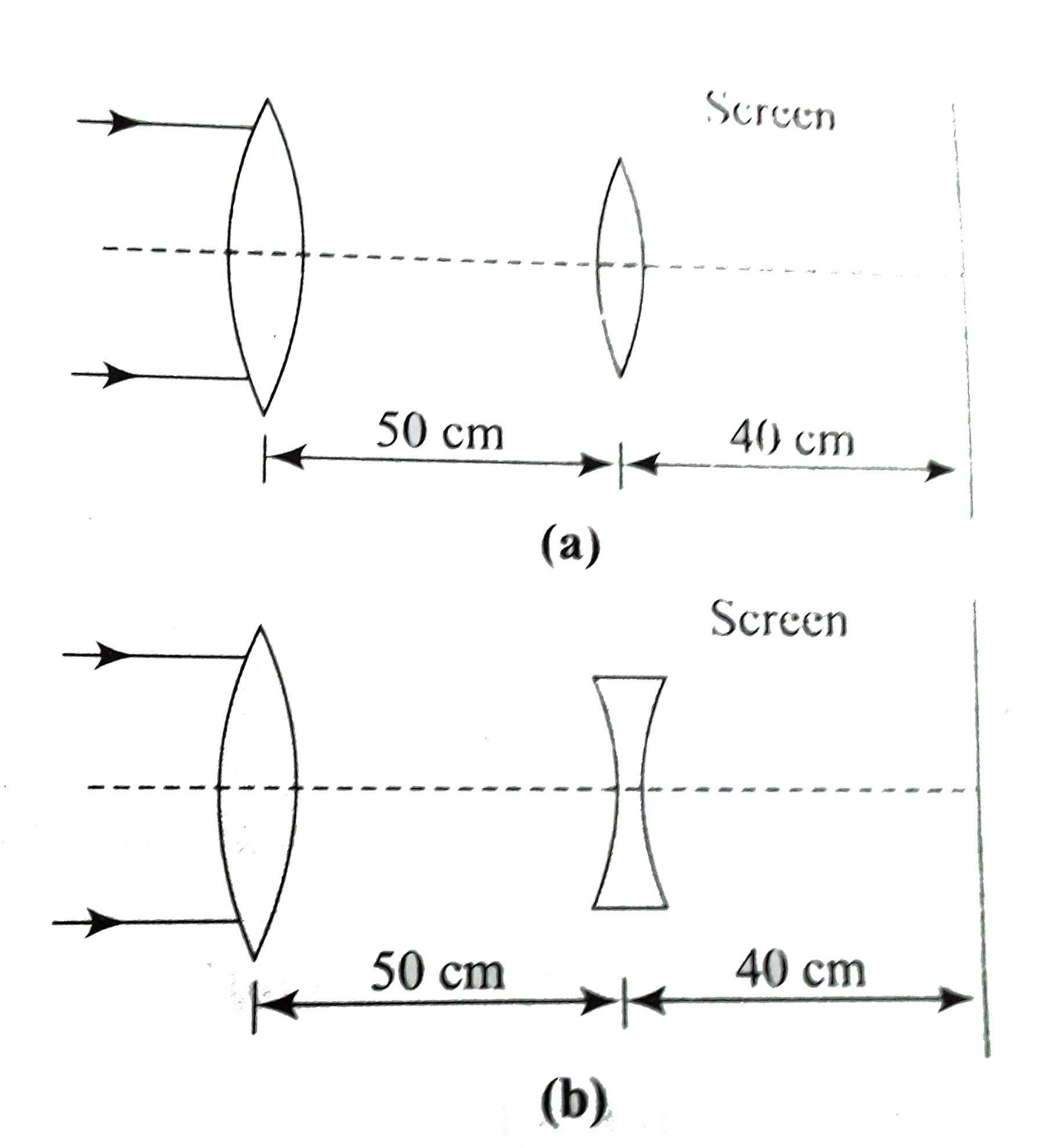
Q. Compare the area illuminated by the beam of light on the screen, which passes through the second lens in the two cases. The ratio (A2/A1) will beView SolutionA convex lens of focal length 40 cm is in contact with a concave lens of focal length 25 cm. The power of the combination is
View SolutionA convex lens of focal length 80 cm and a concave lens of focal length 50 cm are combined toghether. What will be their resulting power ?
View SolutionA thin convex lens of focal length 20 cm is kept in contact with a thin concave lens of focal length 15 cm. Find the focal length and the nature of the combination.
View SolutionA converging lens of focal length 40 cm is kept in contact with a diverging lens of focal length 30 cm. Find the focal length of the combination.
View SolutionA convex lens A of focal length 20cm and a concave lens B of focal length 10 cm are kept along the same axis with a distance d between them. If a parallel beam, then d is
View SolutionA convex lens A of focal length 20cm and a concave lens B of focal length 10 cm are kept along the same axis with a distance d between them. If a parallel beam, then d is
View SolutionA convex lens of power +2.5D is in contact with a concave lens of focal length 25 cm. The power of combination is
View SolutionWhat is the focal length of a convex lens of focal length 30cm in contact with a concave lens of focal length 20cm. Is the system a converging or a diverging lens ? Ignore thickness of the lenses.
View SolutionAn eye specialist prescribes spectacles having combination of convex lens of focal length 40cm in contact with a concave lens of focal length 25cm. The power of this lens combination in diopters is
View Solution
