A parallel beam of particles of mass m moving with velocity v impinges on a wall at an angle θ to its normal. The number of particles per unit volume in the beam is n. If the collision of particles with the wall is elastic, then the pressure exerted by this beam on the wall is
All the molecules contained in the cylinder of length v and inclined on the wall at an angle θ to the normal will strike the wall every second. Let Δ S be the base area of the cylinder.
The volume of the cylinder =ΔSvcosθ.
Therefore, the number of molecules striking ΔS every second =(ΔSvcosθ×n).
Change of momentum per molecule =2mvcosθ.
∴Pressure=ForceArea=(2mvcosθ)(ΔSvcosθ×n)(ΔScos2θ)=2mv2n
∴p=2×(286.0×1026)(9×1024)×4002×cos230∘
=1.00×105Nm−2=1 atm

Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Solved Examples
14 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.1
20 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
A molecule of mass m moving at a velocity v impinges elastically on the wall at an angle α with the wall. Then
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?

View SolutionA particle of mass m is projected with a velocity v at an angle of θ with horizontal. The angular momentum of the particle at the highest point of its trajectory is equal to :
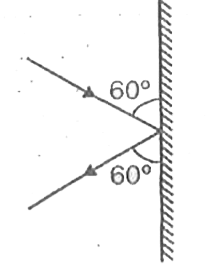
View SolutionA body of mass 3 kg moving with velocity 10 m/s hits a wall at an angle of 60∘ and returns at the same angle. The impact time was 0.2 s. Calculate the force exerted on the wall.
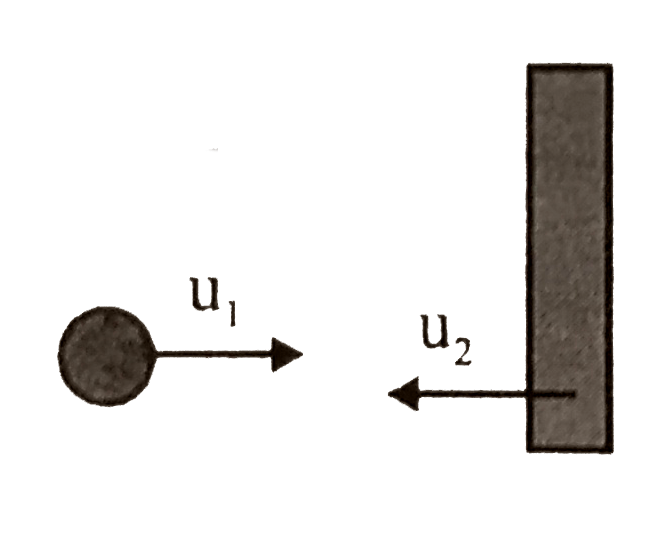
View SolutionA particle of mass m moves with velocity u1=20m/s towards a wall that is moving with velocity u2=5m/s. If the particle collides with the wall without losing its energy, find the speed of particle just after the collision.
View SolutionA particle of mass m moving at a velocity v strikes with the wall at an angle α with the wall and leaves ball making same angle with the wall. Choose the correct statemet (s) from the following.
View SolutionA particle of mass m moving with velocity v makes head-on elastic collision with a sationary particle of mass 2m. Kinetic energy lost by the lighter particle during period of deformation is
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View SolutionA particle of mass m moving with a speed v hits elastically another staionary particle of mass 2m on a smooth horizontal circular tube of radius r. Find the time when the next collision will take place?
View Solution
