A molecule of mass m moving at a velocity v impinges elastically on the wall at an angle α with the wall. Then
the impulsive reaction of the wall is 2mvcosα
the impulsive reaction of the wall is 2mvsinα
the impulsive reaction of the wall is nonzero
given data is insufficient to calculate impulsive reaction of the wall
The correct Answer is:B
To solve the problem of a molecule of mass m moving at a velocity v impinging elastically on a wall at an angle α, we can follow these steps:
Step 1: Resolve the Velocity Components
The velocity v of the molecule can be resolved into two components:
- The component perpendicular to the wall: v⊥=vsinα
- The component parallel to the wall: v∥=vcosα
Step 2: Determine Initial Momentum
The initial momentum of the molecule before the collision can be calculated using the perpendicular component since only this component will change direction upon collision:
pinitial=mv⊥=m(vsinα)
Step 3: Determine Final Momentum
Since the collision is elastic, the component of velocity perpendicular to the wall will reverse direction while the parallel component remains unchanged. Therefore, the final momentum after the collision is:
pfinal=−mv⊥+mv∥=−m(vsinα)+m(vcosα)
However, since we are interested in the change in momentum only in the perpendicular direction:
pfinal=−m(vsinα)
Step 4: Calculate Change in Momentum
The change in momentum (Δp) is given by:
Δp=pfinal−pinitial=−m(vsinα)−m(vsinα)=−2m(vsinα)
Step 5: Calculate the Impulsive Reaction Force
The impulsive reaction force F exerted by the wall on the molecule can be calculated using the formula for force as the rate of change of momentum:
F=ΔpΔt
Assuming the time duration of the collision Δt is very small, we can express the impulsive force as:
F=−2m(vsinα)/Δt
This force acts in the direction opposite to the initial momentum of the molecule.
Conclusion
The impulsive reaction force exerted by the wall on the molecule is:
F=−2m(vsinα)/Δt
In terms of magnitude, we can express it as:
|F|=2m(vsinα)Δt
The velocity v of the molecule can be resolved into two components:
- The component perpendicular to the wall: v⊥=vsinα
- The component parallel to the wall: v∥=vcosα
The initial momentum of the molecule before the collision can be calculated using the perpendicular component since only this component will change direction upon collision:
pinitial=mv⊥=m(vsinα)
Since the collision is elastic, the component of velocity perpendicular to the wall will reverse direction while the parallel component remains unchanged. Therefore, the final momentum after the collision is:
pfinal=−mv⊥+mv∥=−m(vsinα)+m(vcosα)
However, since we are interested in the change in momentum only in the perpendicular direction:
pfinal=−m(vsinα)
The change in momentum (Δp) is given by:
Δp=pfinal−pinitial=−m(vsinα)−m(vsinα)=−2m(vsinα)
The impulsive reaction force F exerted by the wall on the molecule can be calculated using the formula for force as the rate of change of momentum:
F=ΔpΔt
Assuming the time duration of the collision Δt is very small, we can express the impulsive force as:
F=−2m(vsinα)/Δt
This force acts in the direction opposite to the initial momentum of the molecule.
The impulsive reaction force exerted by the wall on the molecule is:
F=−2m(vsinα)/Δt
In terms of magnitude, we can express it as:
|F|=2m(vsinα)Δt
Similar Questions
A particle of mass m moving at a velocity v strikes with the wall at an angle α with the wall and leaves ball making same angle with the wall. Choose the correct statemet (s) from the following.
View SolutionA parallel beam of particles each of mass m moving with velocity v impinges on a wall at an angle θ to its normal. The number of particles per unit volume in the beam is n. If the collision of particles with the wall is elastic, then the pressure exerted by this beam on the wall is
View SolutionA heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.

View SolutionA body of mass m moving with velocity uˆi collides elastically with a body at rest of mass 3m and then the final velocity of body mass m is v ˆj. Find the relation between v and u
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
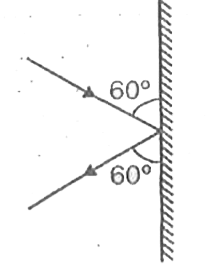
View SolutionA body of mass 3 kg moving with velocity 10 m/s hits a wall at an angle of 60∘ and returns at the same angle. The impact time was 0.2 s. Calculate the force exerted on the wall.
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA particle of mass m strikes elastically on a wall with velocity v, at an angle of 60∘ from the wall then magnitude of change in momentum of ball along the wall is
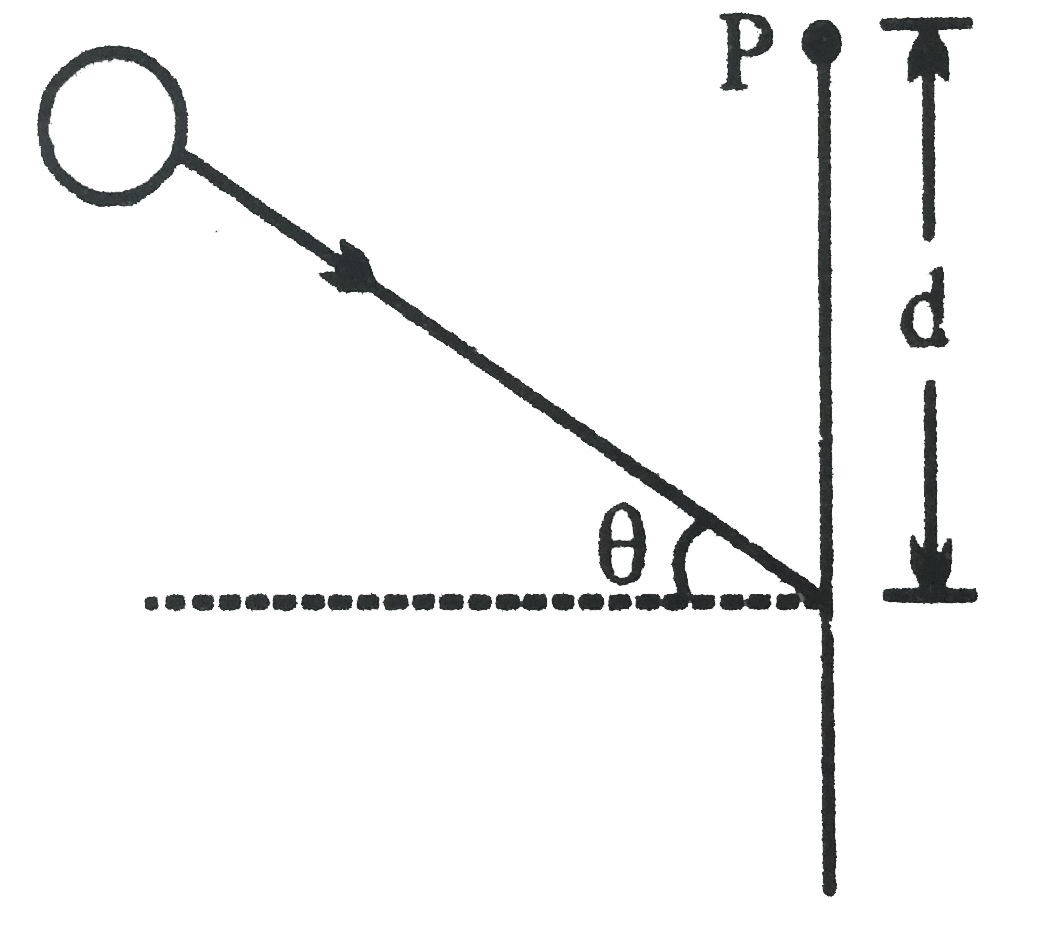
View SolutionA ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is :
 .
.
View Solution
