A particle of mass m moving at a velocity v strikes with the wall at an angle α with the wall and leaves ball making same angle with the wall. Choose the correct statemet (s) from the following.
The impulsive reaction of wall is 2mV sin α
The impulsive reaction of wall is zero
The coefficient of restitution ≠1
There is no force by particle on the wall
The correct Answer is:A
To solve the problem, we need to analyze the collision of a particle with a wall at an angle and determine the impulse and the coefficient of restitution.
1. Understanding the Collision:
- A particle of mass m is moving with velocity v and strikes a wall at an angle α.
- After the collision, the particle leaves the wall making the same angle α with the wall.
2. Components of Velocity:
- Before the collision, the velocity components of the particle can be expressed as:
- vx=vcosα (along the wall)
- vy=vsinα (perpendicular to the wall)
- After the collision, the components of the velocity will be:
- v′x=v′cosα (along the wall)
- v′y=−v′sinα (since the direction changes)
3. Conservation of Momentum:
- Since there are no external forces acting along the line of impact, momentum is conserved.
- The initial momentum along the y-direction (perpendicular to the wall) is:
pinitial=mvy=mvsinα
- The final momentum along the y-direction after the collision is:
pfinal=−mv′sinα
- Setting initial momentum equal to final momentum:
mvsinα=−mv′sinα
- This simplifies to:
v′=−v
4. Calculating Impulse:
- Impulse is defined as the change in momentum.
- The change in momentum along the y-direction is:
Δp=pfinal−pinitial=−mvsinα−mvsinα=−2mvsinα
- The impulse reaction of the particle on the wall is:
J=2mvsinα
5. Coefficient of Restitution:
- The coefficient of restitution e is defined as the ratio of the velocity of separation to the velocity of approach.
- The velocity of separation (after collision) is:
vseparation=−v′sinα=vsinα
- The velocity of approach (before collision) is:
vapproach=vsinα
- Therefore, the coefficient of restitution is:
e=vseparationvapproach=vsinαvsinα=1
6. Conclusion:
- The impulse reaction of the ball is 2mvsinα.
- The coefficient of restitution is equal to 1.
Final Answers:
- The correct statement is:
- The impulse reaction of the ball is 2mvsinα (Option 1 is correct).
- The coefficient of restitution is equal to 1 (Option 3 is incorrect).
- A particle of mass m is moving with velocity v and strikes a wall at an angle α.
- After the collision, the particle leaves the wall making the same angle α with the wall.
- Before the collision, the velocity components of the particle can be expressed as:
- vx=vcosα (along the wall)
- vy=vsinα (perpendicular to the wall)
- After the collision, the components of the velocity will be:
- v′x=v′cosα (along the wall)
- v′y=−v′sinα (since the direction changes)
- Since there are no external forces acting along the line of impact, momentum is conserved.
- The initial momentum along the y-direction (perpendicular to the wall) is:
pinitial=mvy=mvsinα
- The final momentum along the y-direction after the collision is:
pfinal=−mv′sinα
- Setting initial momentum equal to final momentum:
mvsinα=−mv′sinα
- This simplifies to:
v′=−v
- Impulse is defined as the change in momentum.
- The change in momentum along the y-direction is:
Δp=pfinal−pinitial=−mvsinα−mvsinα=−2mvsinα
- The impulse reaction of the particle on the wall is:
J=2mvsinα
- The coefficient of restitution e is defined as the ratio of the velocity of separation to the velocity of approach.
- The velocity of separation (after collision) is:
vseparation=−v′sinα=vsinα
- The velocity of approach (before collision) is:
vapproach=vsinα
- Therefore, the coefficient of restitution is:
e=vseparationvapproach=vsinαvsinα=1
- The impulse reaction of the ball is 2mvsinα.
- The coefficient of restitution is equal to 1.
- The correct statement is:
- The impulse reaction of the ball is 2mvsinα (Option 1 is correct).
- The coefficient of restitution is equal to 1 (Option 3 is incorrect).
Similar Questions
A molecule of mass m moving at a velocity v impinges elastically on the wall at an angle α with the wall. Then
View SolutionA ball of mass 600 gm strikes a wall with a velocity of 5ms−1 at an angle 30∘ with the wall and rebounds with the same speed at the same angle with the wall. The change in momentum of the ball is, (in kg ms−1)
View SolutionA 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60o with the wall and reflects at the same angle. If it remains in contact with the wall for 0.1 s, then the force is
View SolutionA body of mass 3 kg moving with velocity 10 m/s hits a wall at an angle of 60∘ and returns at the same angle. The impact time was 0.2 s. Calculate the force exerted on the wall.
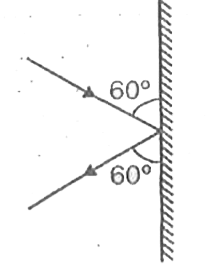
View SolutionA parallel beam of particles each of mass m moving with velocity v impinges on a wall at an angle θ to its normal. The number of particles per unit volume in the beam is n. If the collision of particles with the wall is elastic, then the pressure exerted by this beam on the wall is
View SolutionA particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
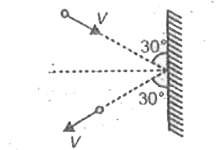
View SolutionA particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
View SolutionA ball strikes a wall with a velocity →u at an angle θ with the normal to the wall surface. and rebounds from it at an angle β with the surface. Then
View SolutionA ball of mass 3kg moving with a speed of 100 m/s, strikes a wall at an angle 60∘ (as shown in figure). The ball rebounds at the same speed and remains in contact with the wall for 0.2 s, the force exerted by the ball on the wall is

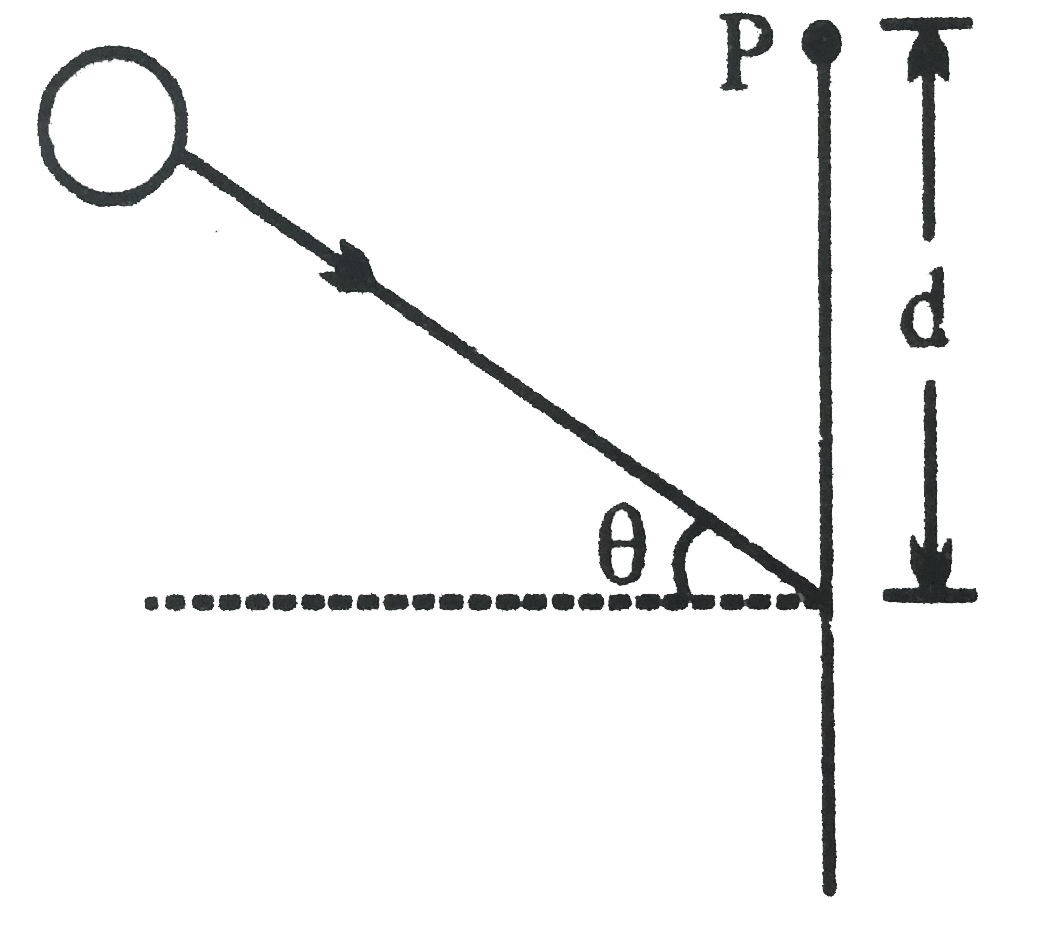
View SolutionA ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is :
 .
.
View Solution
