A parallel plate capacitor has plate separation d and capacitance 25μF. If a metallic foil of thickness 27d is introduced betwenn the plates, the capacitance would become
25μF
35μF
1257μF
1752μF
The correct Answer is:B, C
To solve the problem, we need to find the new capacitance of a parallel plate capacitor after introducing a metallic foil of thickness 27d between the plates. The initial capacitance is given as 25μF.
1. Understanding the Initial Setup:
- The initial capacitance C0 of a parallel plate capacitor is given by the formula:
C0=Aϵ0d
- Here, A is the area of the plates, ϵ0 is the permittivity of free space, and d is the separation between the plates.
2. Introducing the Metallic Foil:
- A metallic foil of thickness t=27d is introduced between the plates.
- When a metallic conductor is placed between the plates of a capacitor, the electric field inside the conductor becomes zero.
3. Calculating the Effective Distance:
- The effective distance between the plates where the electric field exists is now reduced to:
d′=d−t=d−27d=57d
4. Finding the New Capacitance:
- The new capacitance C can be calculated using the modified distance d′:
C=Aϵ0d′
- Substitute d′ into the equation:
C=Aϵ057d=7Aϵ05d
5. Relating New Capacitance to Initial Capacitance:
- From the initial capacitance C0=Aϵ0d=25μF, we can express Aϵ0 as:
Aϵ0=25d
- Substitute this into the new capacitance equation:
C=7⋅25d5d=7⋅255=35μF
Final Answer:
The new capacitance after introducing the metallic foil is 35μF.
---
- The initial capacitance C0 of a parallel plate capacitor is given by the formula:
C0=Aϵ0d
- Here, A is the area of the plates, ϵ0 is the permittivity of free space, and d is the separation between the plates.
- A metallic foil of thickness t=27d is introduced between the plates.
- When a metallic conductor is placed between the plates of a capacitor, the electric field inside the conductor becomes zero.
- The effective distance between the plates where the electric field exists is now reduced to:
d′=d−t=d−27d=57d
- The new capacitance C can be calculated using the modified distance d′:
C=Aϵ0d′
- Substitute d′ into the equation:
C=Aϵ057d=7Aϵ05d
- From the initial capacitance C0=Aϵ0d=25μF, we can express Aϵ0 as:
Aϵ0=25d
- Substitute this into the new capacitance equation:
C=7⋅25d5d=7⋅255=35μF
The new capacitance after introducing the metallic foil is 35μF.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises17videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.520videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery37videos
ELECTROSTATICS
Similar Questions
A sheet of aluminium foil of negligible thickness is introduced between the plates of a capacitor. The capacitance of the capacitor
View SolutionSeparation between the plates of a parallel plate capacitor is d and the area of each plates is A. When a slab of material of dielectric constant k and thickness t(t<d) is introduced between the plates. Its capacitance becomes
View Solution
Knowledge Check
- Question 1 - Select One
A parallel plate capacitor with air between the plates has a capacitance of 10 pF. The capacitance, if the distance bgetween the plates is reduced by half and the space between tehm is filled with a substance of dielectric constant 4 is
A80pFB96pFC100pFD120pF
The two plates of a parallel plate capacitor are 4mm apart. A slab of dielectric constant 3 and thickness 3mm is introduced between the plates is so adjusted that the capacitance of the capacitor becomes 23rd of its original value. What is the new distance between the plates ?
View SolutionA parallel plate capacitor consists of two metal plates of area A and separation d. A slab of thickness t and electric constant K is inserted between the plates with its faces parallel to the plates and having the same surface area as that of the plates. Find the capacitance of the system.
IF K=2, for what value of t/d will the capacitance of the system be 3/2 times that of the air capacitor? Calculate the energy in the two cases and account for the energy change.
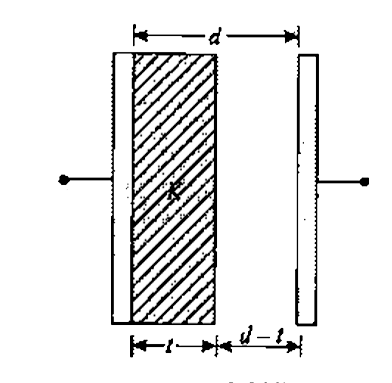 View Solution
View SolutionA parallel plate capacitor has plate area A and plate separation d. The space betwwen the plates is filled up to a thickness x (ltd) with a dielectric constant K. Calculate the capacitance of the system.
 View Solution
View SolutionA pararllel plate capacitor has plates of area A and separation d and is charged to potential diference V. The charging battery is then disconnected and the plates are pulle apart until their separation is 2d. What is the work required to separate the plates?
View SolutionA parallel plate capacitor with air as the dielectric has capacitance C. A slab of dielectric constant K and having the same thickness as the separation between plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. The new capacitance will be :
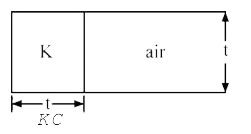 View Solution
View SolutionA parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
View SolutionA parallel plate capacitor with air between the plates has capacitance of 9pF. The separation between its plates is 'd'. The space between the plates is now filled with two dielectrics. One of the dielectrics has dielectric constant k1=3 and thickness d3 while the other one has dielectric constant k2=6 and thickness 2d3. Capacitance of the capacitor is now
View Solution

