A parallel plate capacitor of capacitance 10μF is connected across a battery of emf 5 mV. Now, the space between the plates of the capacitors is filled with a deielectric material of dielectric constant K=5. Then, the charge that will flow through the battery till equilibrium is reached is
250μC
250nC
200nC
200μC
The correct Answer is:C
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the initial charge stored in the capacitor
The initial charge Q stored in a capacitor is given by the formula:
Q=C×V
where:
- C is the capacitance,
- V is the voltage (emf of the battery).
Given:
- C=10μF=10×10−6F
- V=5mV=5×10−3V
Substituting the values:
Q=(10×10−6)×(5×10−3)=50×10−9C=50nC
Step 2: Calculate the new capacitance after inserting the dielectric
When a dielectric material is inserted between the plates of a capacitor, the new capacitance C′ can be calculated using the formula:
C′=K×C
where K is the dielectric constant.
Given:
- K=5
Substituting the values:
C′=5×(10×10−6)=50×10−6F=50μF
Step 3: Calculate the new charge stored in the capacitor with the dielectric
The new charge Q′ stored in the capacitor after the dielectric is inserted is given by:
Q′=C′×V
Substituting the values:
Q′=(50×10−6)×(5×10−3)=250×10−9C=250nC
Step 4: Calculate the charge that flows through the battery
The charge that flows through the battery until equilibrium is reached is the difference between the new charge and the initial charge:
ΔQ=Q′−Q
Substituting the values:
ΔQ=250nC−50nC=200nC
Final Answer
The charge that will flow through the battery till equilibrium is reached is:
ΔQ=200nC
---
The initial charge Q stored in a capacitor is given by the formula:
Q=C×V
where:
- C is the capacitance,
- V is the voltage (emf of the battery).
- C=10μF=10×10−6F
- V=5mV=5×10−3V
Q=(10×10−6)×(5×10−3)=50×10−9C=50nC
When a dielectric material is inserted between the plates of a capacitor, the new capacitance C′ can be calculated using the formula:
C′=K×C
where K is the dielectric constant.
- K=5
C′=5×(10×10−6)=50×10−6F=50μF
The new charge Q′ stored in the capacitor after the dielectric is inserted is given by:
Q′=C′×V
Q′=(50×10−6)×(5×10−3)=250×10−9C=250nC
The charge that flows through the battery until equilibrium is reached is the difference between the new charge and the initial charge:
ΔQ=Q′−Q
ΔQ=250nC−50nC=200nC
The charge that will flow through the battery till equilibrium is reached is:
ΔQ=200nC
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type8videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type94videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
Two parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionHalf of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
View SolutionA parallel plate capacitar, of capacitance, 20μF, is connected to a 100 V supply. After some time, the battery is disconnected , and the space, between the plates of the capacitor is filled with a dielectric, of dielectric constant 5. Calculate the energy stored in the capacitar (i) before (ii)after dielectric has been put in between its plates.
View SolutionThe terminals of a battery of emf V are connected to the two plates of a parallel plate capacitor. If the space between the plates of the capacitor is filled with an insulator of dielectric constant K, then :
View SolutionA parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
View SolutionThe figure shows two identical parallel plate capacitors connected to a battery with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant(or relative permittivity) 3. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.
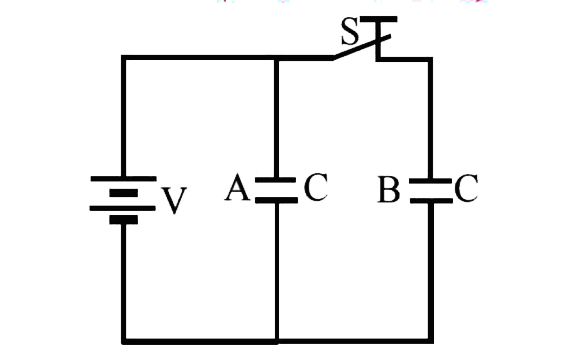View SolutionTwo identical parallel plate capacitors A and B are
connected to a battery of V volts with the switch S
closed . The switch is now opend and the free
space between the plantes of the capacitors is filled
with a dielectric of dielectric constant K. Find the
rario of the total electrostatic energy stored in both
capacitors before and after the introduction of the dielectric.
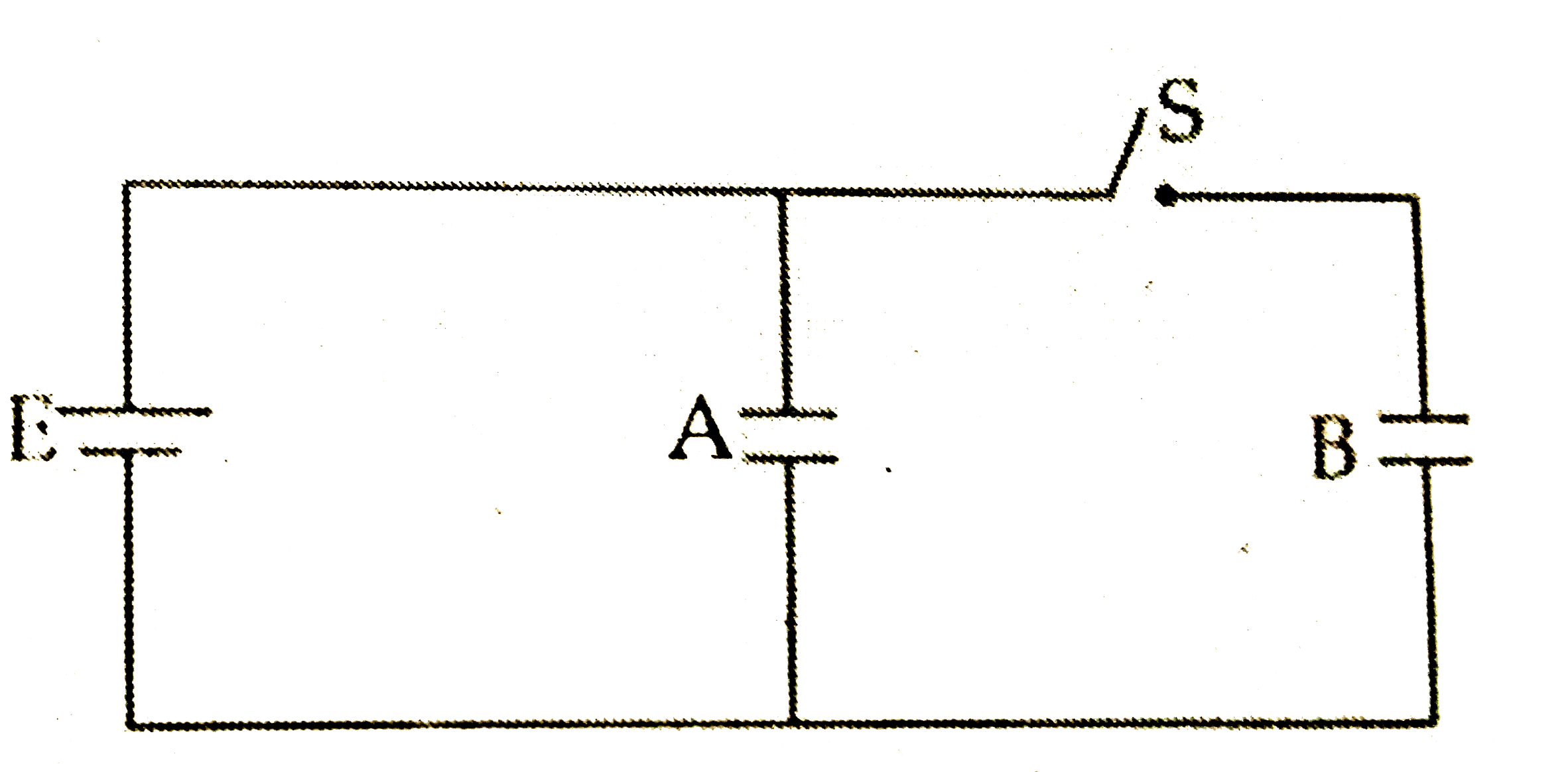View SolutionA parallel plate capacitor of capacitance 90 pF is connected to a battery of emf 20 V. If a dielectric material of dielectric constant K=53 is inserted between the plates, the magnitude of the induced charge will be :
View SolutionThe parallel combination of two air filled parallel plate capacitor of capacitance C and nC is connected to a battery of voltage, V. When the capacitors are fulley charged, the battery is removed and after that a dielectric material of dielectric constant K is placed between the two plates of the first capacitors. the new potential difference of the combined system is
View SolutionTwo identical parallel plate air capacitors are connected in series to a battery of emf V. If one of the capacitor is completely filled with dielectric material of constant K, then potential difference of the other capacitor will become
View Solution