A parallel plate capacitar, of capacitance, , is connected to a 100 V supply. After some time, the battery is disconnected , and the space, between the plates of the capacitor is filled with a dielectric, of dielectric constant 5. Calculate the energy stored in the capacitar (i) before (ii)after dielectric has been put in between its plates.
To solve the problem, we need to calculate the energy stored in a parallel plate capacitor both before and after a dielectric is introduced. Let's go through the calculations step by step.
Step 1: Calculate the energy stored before the dielectric is introduced.
The formula for the energy (U) stored in a capacitor is given by:
U=12CV2
Where:
- C is the capacitance
- V is the voltage
Given:
- C=20μF=20×10−6F
- V=100V
Substituting the values into the formula:
U=12×(20×10−6)×(100)2
Calculating (100)2:
(100)2=10000
Now substituting back:
U=12×(20×10−6)×10000
Calculating further:
U=12×20×10−6×104
U=12×20×10−2
U=10×10−2=0.1J
Step 2: Calculate the energy stored after the dielectric is introduced.
When a dielectric is introduced, the capacitance increases. The new capacitance C′ with a dielectric constant k is given by:
C′=k×C
Given:
- k=5
Calculating C′:
C′=5×(20×10−6)=100×10−6F=100μF
Now, we need to calculate the energy stored in the capacitor after the dielectric is introduced. Since the battery is disconnected, the charge Q remains constant, and we can use the formula:
U′=Q22C′
First, we need to find the charge Q on the capacitor before the dielectric was introduced:
Q=C×V=(20×10−6)×100=2×10−3C
Now substituting Q and C′ into the energy formula:
U′=(2×10−3)22×(100×10−6)
Calculating (2×10−3)2:
(2×10−3)2=4×10−6
Now substituting back:
U′=4×10−62×100×10−6=4×10−6200×10−6=4200=0.02J
Final Results:
- Energy stored before the dielectric: 0.1J
- Energy stored after the dielectric: 0.02J
- C is the capacitance
- V is the voltage
- C=20μF=20×10−6F
- V=100V
U=12×20×10−2
U=10×10−2=0.1J
- k=5
- Energy stored before the dielectric: 0.1J
- Energy stored after the dielectric: 0.02J
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - C.B.S.E.CLASS-XII PHYSICS (THEORY) [SET-I] (SECTION-A)5videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTIONS-B4videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION-C50videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
A parallel plate capacitor of capacitance 10μF is connected across a battery of emf 5 mV. Now, the space between the plates of the capacitors is filled with a deielectric material of dielectric constant K=5. Then, the charge that will flow through the battery till equilibrium is reached is
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V and then disconnected with the battery. If separation between the plates is decreased by 50% and the space between the plates is filled with a dielectric slab of dielectric constant K=10. then
View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionHalf of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
View SolutionThe terminals of a battery of emf V are connected to the two plates of a parallel plate capacitor. If the space between the plates of the capacitor is filled with an insulator of dielectric constant K, then :
View SolutionAnswer the following:
(a) When a parallel plate capacitor is connected across a dc battery, explain briefly how the capacitor gets charged.
(b) A parallel plate capacitor of capacitance 'C' is charged to 'V' volt by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant 1<k<2 is introduced to fill the space between the plates. How will the following be affected ?
(i) The electric field between the plates of the capacitor.
(ii) The energy stored in the capacitor. Justify your answer in each case.
(c) The electric potential as a function of distance 'x' is shown in the figure. Draw a graph of the electric field E as a function of x.
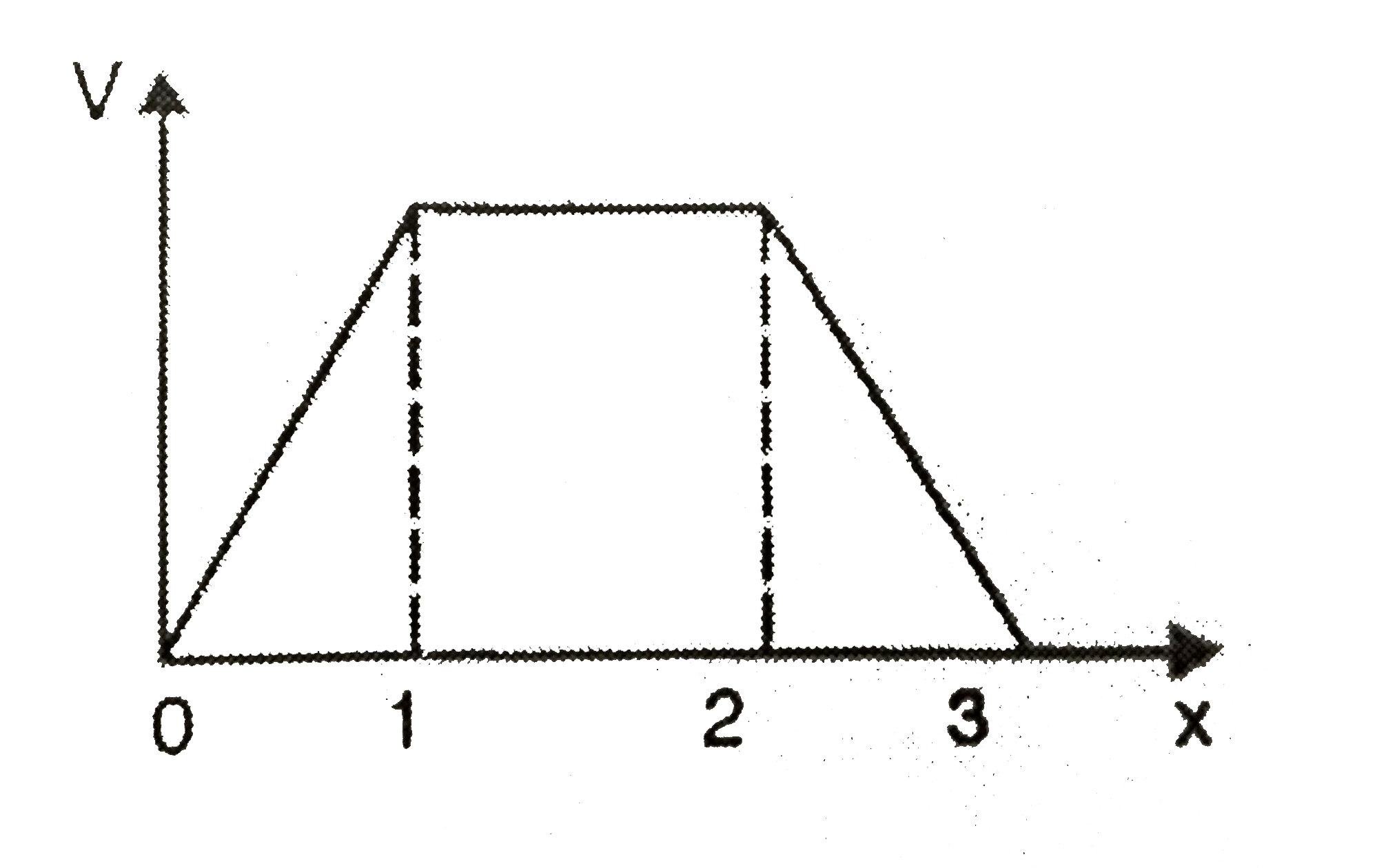 View Solution
View SolutionThe figure shows two identical parallel plate capacitors connected to a battery with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant(or relative permittivity) 3. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.
 View Solution
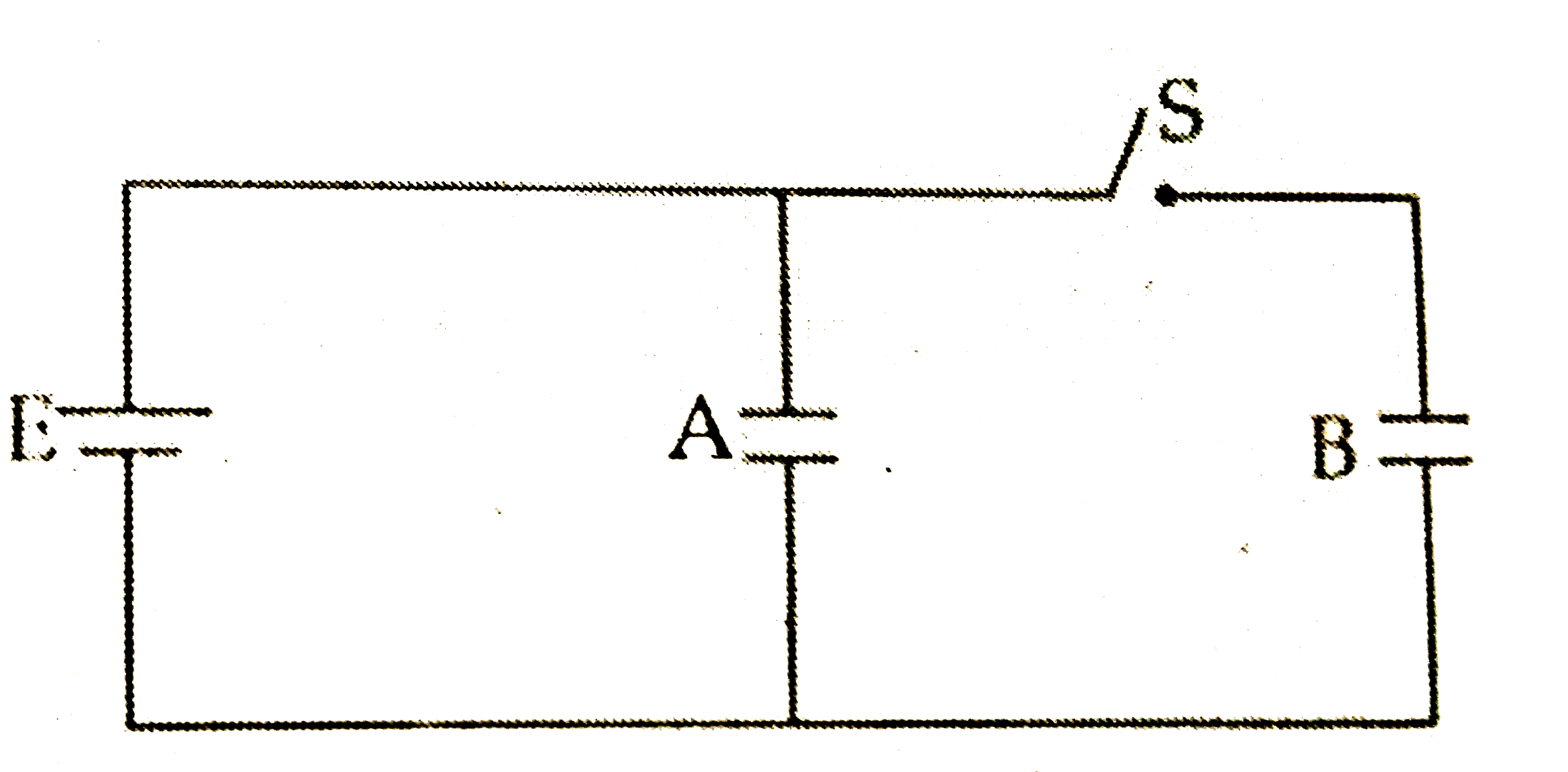
View SolutionTwo identical parallel plate capacitors A and B are
connected to a battery of V volts with the switch S
closed . The switch is now opend and the free
space between the plantes of the capacitors is filled
with a dielectric of dielectric constant K. Find the
rario of the total electrostatic energy stored in both
capacitors before and after the introduction of the dielectric.
 View Solution
View SolutionA parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
View SolutionA parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
 View Solution
View Solution

