A paricle of mass 200g executes a simple harmonic motion. The restorting force is provided by a spring of spring constant 80N/m. Find the time period.
0.31 s
0.21 s
0.11 s
0.25 s
The correct Answer is:A
The time period is
T=2π√mk
=2π⎛⎜
⎜⎝√200x10−3kg80Nm−1⎞⎟
⎟⎠
2πx0.05s=0.31s
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Worked Out Examples
22 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Short Answer
13 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
A block of mass 5 kg executes simple harmonic motion under the restoring force of a spring. The amplitude and the time period of the motion are 0.1 m and 3.14 s respectively. Fnd the maximum force exerted by the spring on the block.
View SolutionA particle at the end of a spring executes simple harmonic motion with a period t1 while the corresponding period for another spring is t2 if the oscillation with the two springs in series is T then
View Solution
Knowledge Check
A particle executes simple harmonic motion under the restoring force provided by a spring. The time period is T. If the spring is divided in two equal parts and one part isused to continue the simple harmonic motion, the time period will
Aremain TBbecoem 2TCbecome T/2Dbecome T√2A block of mass 2kg executes simple harmonic motion under the reading from at a spring .The angular and the time period of motion are 0.2cm and 2πsec respectively Find the maximum force execute by the spring in the block.
A0.05NB0.002NC0.003ND0.004NA mass m oscillates with simple harmonic motion with frequency f=ω2πand amlitude A on a spring with constant K. therefore
Athe total energy of the system is 12KA2BThe frequency is 12π√KMCThe maximum velocity occurs, when x=0Dall the above are correct
A particle of mass 0.50 kg executes a simple harmonic motion under a force F = – (50 N/m)x. If it crosses the centre of oscillation with a speed of 10 m/s, find the amplitude of the motion.
View SolutionA body of mass 0.01 kg executes simple harmonic motion about x = 0 under the influence of a force as shown in figure. The time period of SHM is
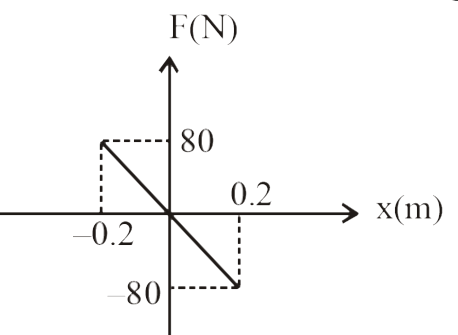
View SolutionA mass M is suspended from a spring of negligible mass. The spring is pulled a little then released, so that the mass executes simple harmonic motion of time period T. If the mass is increased by m, the time period becomes 5T3. Find the ratio of m/M.
View SolutionA mass m oscillates with simple harmonic motion with frequency f=ω2π and amplitude A on a spring of stiffness constant K. Which of the following is not correct ?
View SolutionA particle at the end of a spring executes simple harmonic motion with a period t1 while the corresponding period for another spring is t2 if the oscillation with the two springs in series is T then
View Solution
