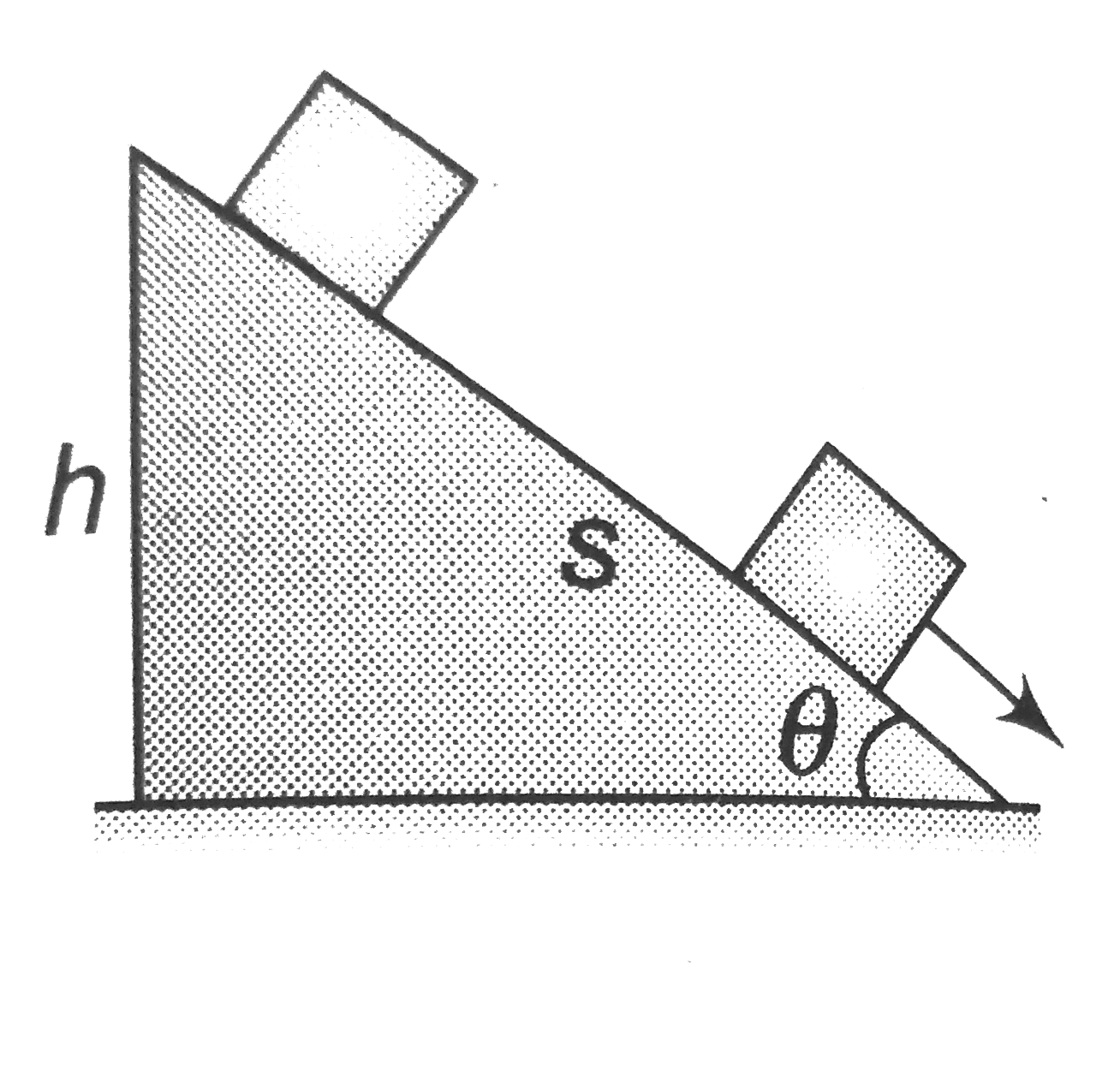
A partical is realeased from the top of two inclined rought surface of height $h$ each. The angle of inclination of the two planes are $30^{\circ}$ and $60^{\circ}$ respectively. All other factors (e.g. coefficient of friction , mass of the block etc) are same in both the cases. Let $K_{1} and K_{2}$ be the kinetic energy of the partical at the bottom of the plane in two cases. Then

A

$K_{1} = K_{2}$

B

$K_{1} > K_{2}$

C

$K_{1} < K_{2}$

D

data insufficient

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Work done in frictioin is
$W = (μ m g cos θ) s$
$= (μ m g cos θ) (\frac{h}{sin θ}) M$
Now ${cos θ}_{1} = {cos 30}^{\circ} = \sqrt{3}$
and ${cos θ}_{2} = {cos 60}^{\circ} = \frac{1}{\sqrt{3}}$
$∴ W_{1} < W_{2}$
i.e., kineyic energy in first case will be less.
$(K = m g h - W)$
or $K_{1} < K_{2}$
.

|

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A block of mass $m$ is released from the top of a mooth inclined plane of height $h$ its speed at the bottom of the plane is proportion to
A $m^{0}$
B $m$
C $m^{2}$
D $m^{- 1}$
Question 2 - Select One
A block is placed on an inclined plane. The angle of inclination of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is
A $sin θ$
B $cos θ$
C $cot θ$
D $tan θ$
Question 3 - Select One
A disc of mass 3 kg rolls down an inclined plane of height 5 m. The translational kinetic energy of the disc on reaching the bottom of the inclined plane is
A50 J
B100 J
C150 J
D175 J

A2Z-WORK, ENERGY, POWER AND COLLISION-Problems Based On Mixed Concepts

Home
Ask Doubt
Profile