A particle at the edge of a ratating disc speeds up at a uniform angular acceleration ∝. If the radius of the disc is R, find the angular distance covered by the particle till its acquires a total acceleration a0.
The angular displacement of the particle till it attains velocity ω is
θ=ω2−ω202∝
where ω0=0 (because the particle starts from rest)
Then, θ=ω2−ω202∝
Let us calculate ω
The total acceleration of the particle is
a=√a2t+a2r
where at=R∝andar=Rω2
If the maximum acceleration of the particle is a0, we have
a0=√R2∝2+R2ω4 ltbrlt This gives ω=(a20−R2θ22R∝)14
Substituting ω from Eq. (ii) in Eq. (i), we have
θ=√a20−R2∝22R∝.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective40videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct76videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.312videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
Refering to v−s diagram, find:
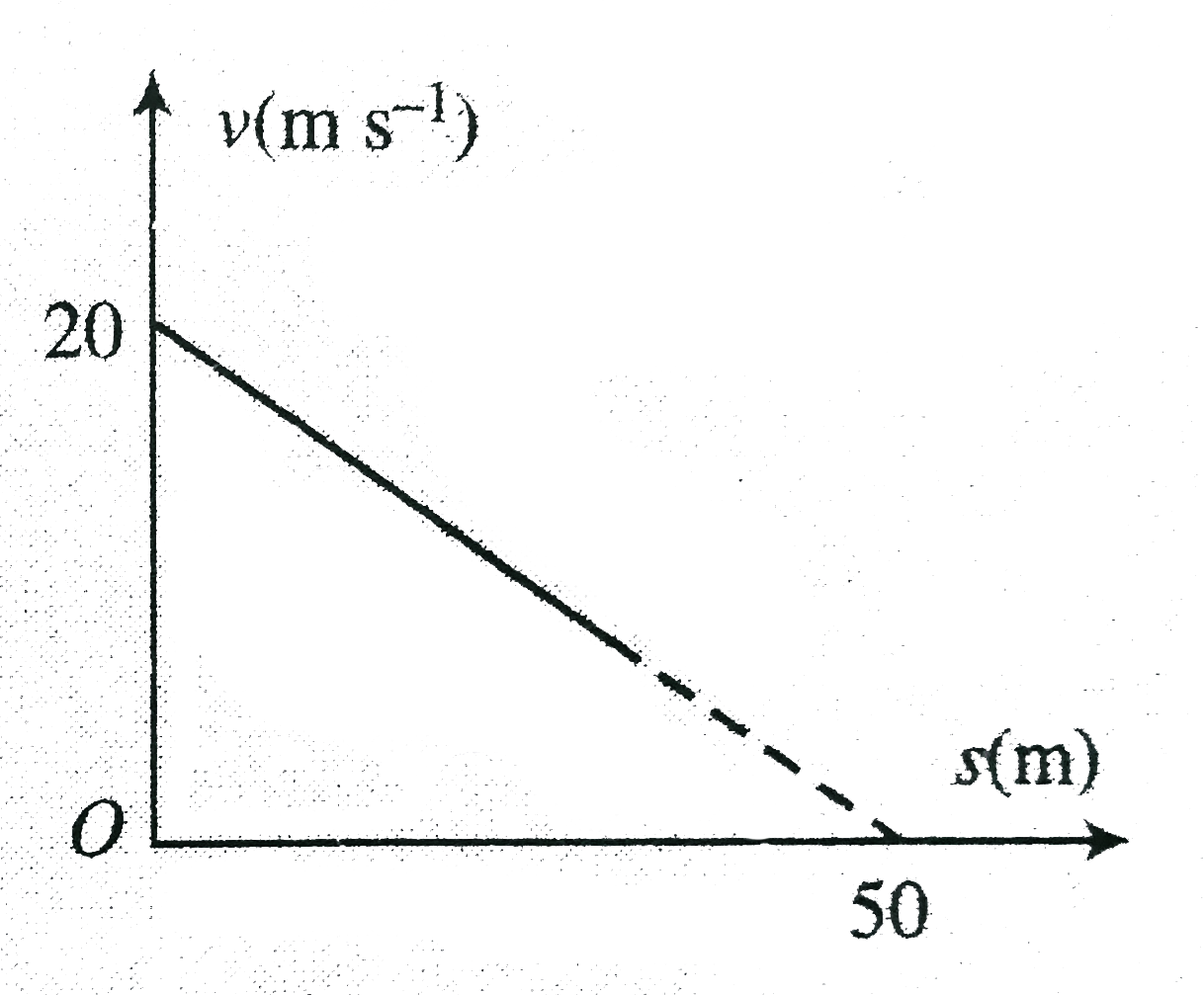 .
.
a. Acceleration of the particle when its velocity becomes half of the initial velocity.
b. Total distance covered by the particle.View SolutionA particle moves along a circular path a radius 15 cm with a constant angular acceleration of 4 "rad/s"^(2). If the initial angular speed of the particle was 5 rad/s. Find its angular displacement in 5 seconds.
View Solution
Knowledge Check
- Question 1 - Select One
A particle is at a distance r from the axis of rotation. A given torque τ produces some angular acceleration in it. If the mass of the particle is doubled and its distance from the axis is halved, the value of torque to produce the same angular acceleration is -
Aτ/2BτC2τD4τ - Question 2 - Select One
A particle is moving around a circular path with uniform angular speed (x) . The radius of the circular path is (r). The acceleration of the particle is:
Ax2rBxrCrx2Drx - Question 3 - Select One
If a tangential force mg is applied to a disc of mass m and radius r, the angular acceleration produced in it is?
AgrBg/rC2grD2gr
A particle is revolving in a circle of radius 1 m with an angular speed of 12 rad/s. At t = 0, it was subjected to a constant angular acceleration α and its angular speed increased to (480π) rotation per minute (rpm) in 2 sec. Particle then continues to move with attained speed. Calculate
(i) angular acceleration of the particle,
(ii) tangential velocity of the particle as a function of time.
(iii) acceleration of the particle at t = 0.5 second and at t = 3 second
(iv) angular displacement at t = 3 second.View SolutionA coin is placed at the edge of a horizontal disc rotating about a vertical axis through its axis with a uniform angular speed 2 rad s−1. The radius of the disc is 50 cm. Find the minimum coefficient of friction between disc and coin so that the coin does not slip. (Take g=10m/s2)
View SolutionA particle starts moving at t = 0 in a circle of radius R=2m with constant angular acceleration of a−3rad/sec2. Initial angular speed of the particle is 1 rad/sec. At time t0 the angle between the acceleration vector and the velocity vector of the particle is 37∘.
What is the value of t0 ?View SolutionIf a particle moves with uniform speed its tangntial acceleration will be
View SolutionIn a non - uniform circular motaion the ratio of tangential to radial acceleration is (where, r= radius of circle, v= speed of the particle, α= angular acceleration)
View Solution

