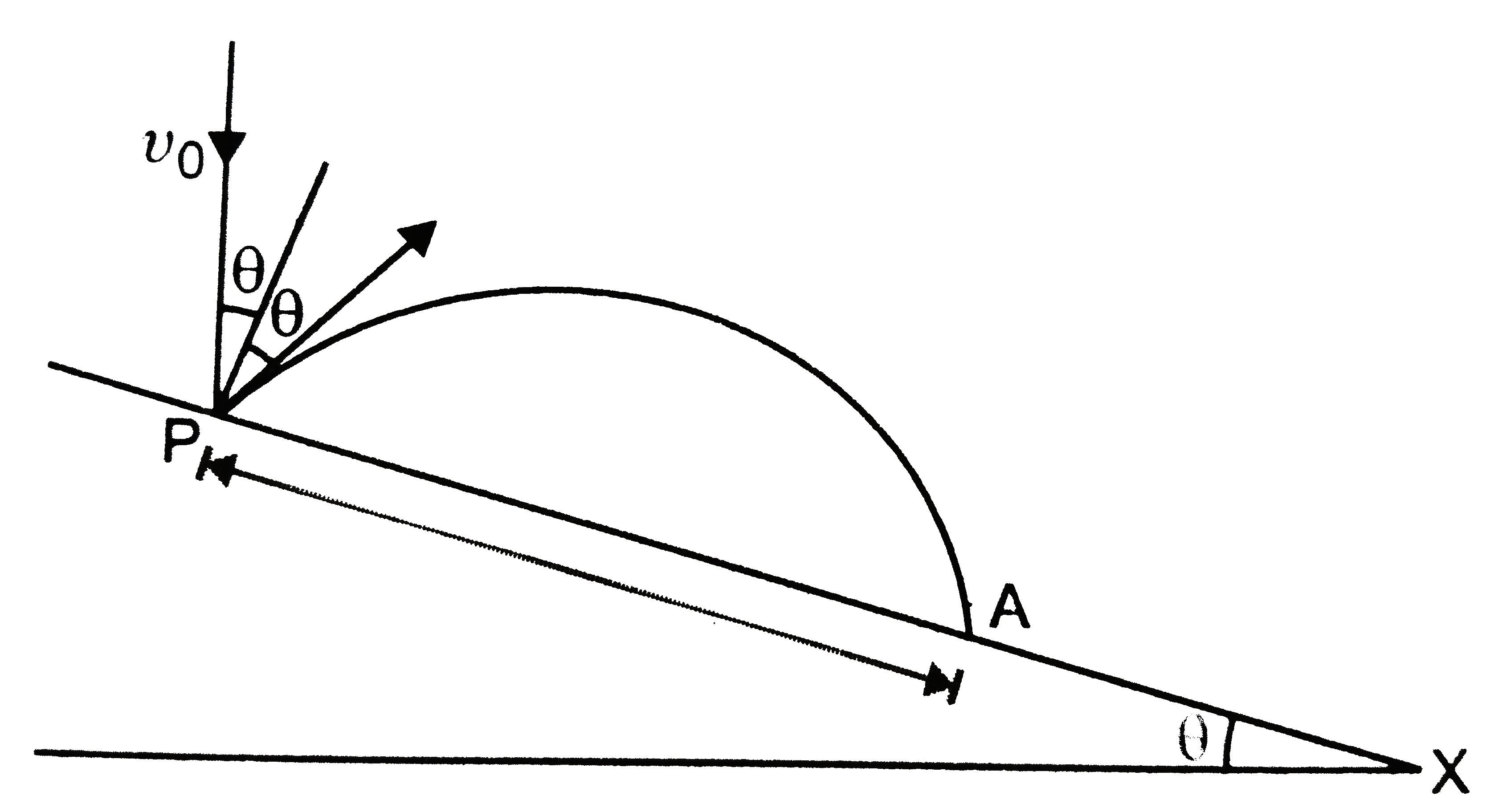
A particle falling vertically from a height hits a plane surface inclined to horizontal at an ange θ with speed v0 and rebounds elastically (Fig. 2 (RP). 28). Find the distance aling the plane where it will hit second time.
 .
.

Considering x and y-axes as shown in the diagram.
For the motion of the projectile from O to A.
y=0,uy=v0cosθ
ay=−gcosθ,t=T
Applying equation of kinematics,
y=uyt+12ayt2
⇒ 0=v0cosθT+12(−gcosθ)T2
⇒ T,[v0cosθ−gcosθT2]=0
T=2v0cosθgcosθ
As T = 0, corresponds to point O
Hence, T=2v0g
Now considering motion along OX.
x=L,ux=v0sinθ,ax=gsinθ,t=T=2v0g
Applying equati of kinematics,
x=uxt+12axt2
⇒ L=v0sinθt+12gsinθt2=(v0sinθ)(T)+12gsinθT2
=(v0sinθ)(2v0g)+12gsinθ×(2v0g)2
=2v20gsinθ+12gsinθ×4v20g2=2v20g[sinθ+sinθ]
⇒ L=4v20gsinθ
Topper's Solved these Questions
Similar Questions
A ball starts falling with zero initial velocity on to a smooth inclined plane forming an angle α with the horizontal. Having fallen a distance h, the ball rebounds elastically off the inclined plane. At what distance from the impact point will the ball rebound for the second time ?
View SolutionA ball starts falling with zero initial velocity on to a smooth inclined plane forming an angle α with the horizontal. Having fallen a distance h, the ball rebounds elastically off the inclined plane . At what distance from the impact point will the ball rebound for the second time ?
View Solution
Knowledge Check
- Question 1 - Select One
A ball (initially at rest) falls vertically for 2 s and hits a smooth plane inclined at 30∘ to the horizontal. The coefficient of restitution is 58. The distance along the plane between the first and second impact of the ball is
A40.63 mB20.63 mC30.63 mD50.63 - Question 2 - Select One
A particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)
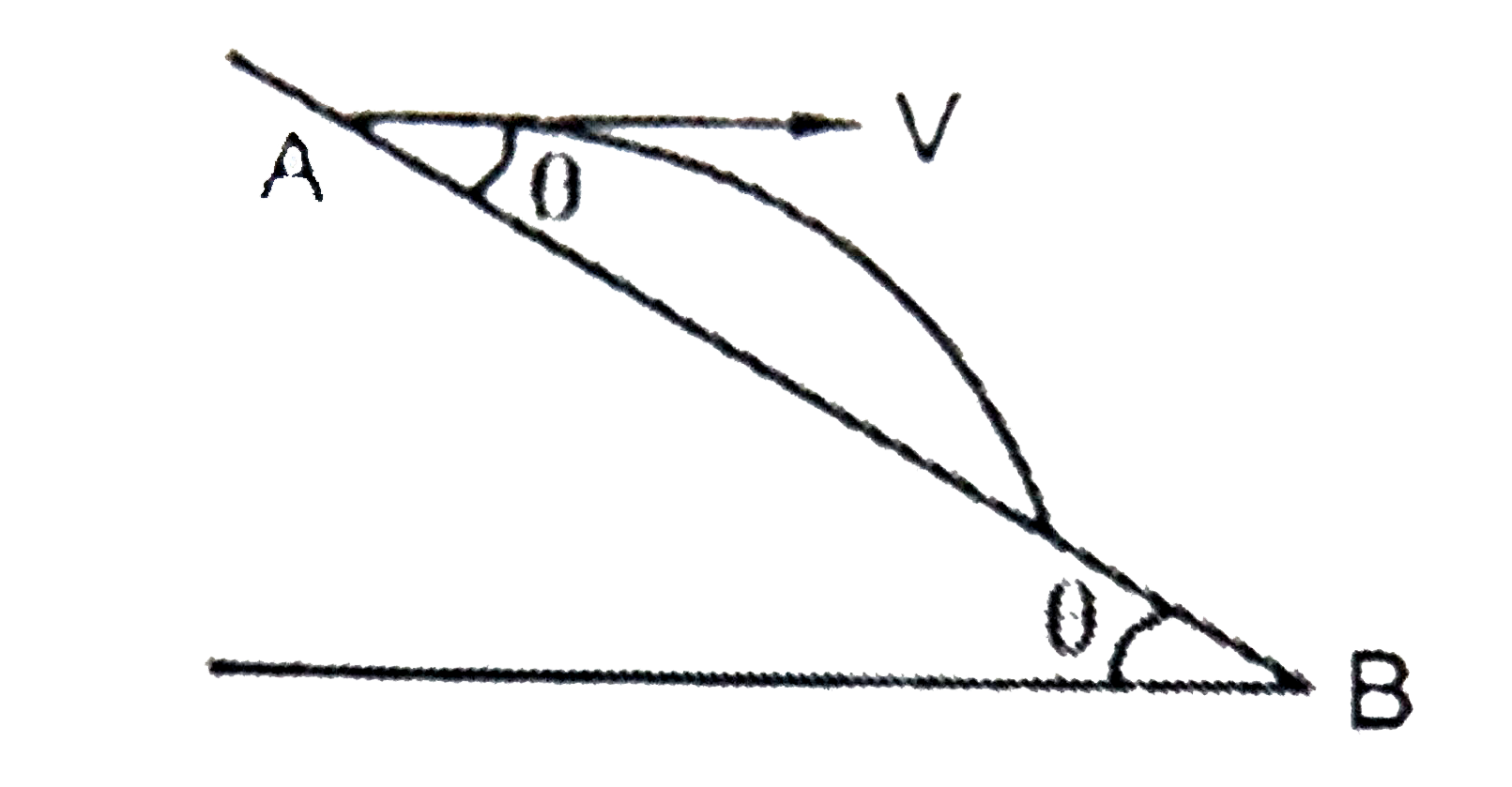
Find the time taken by the particle to hit the plane.A34sB3sC4sD43s - Question 3 - Select One
A ball starts falling freely from a height h from a point on the inclined plane forming an angle α with the horizontal as shown. After collision with the incline it rebounds elastically off the plane. Then it again strikes the incline at
 At=√8hg after it strikes the inclined at ABt=√2hgafter it strikes the inclined at A.Ca distance 4h sin α from A along the inclineDa distance 8h sin α from A along the incline
At=√8hg after it strikes the inclined at ABt=√2hgafter it strikes the inclined at A.Ca distance 4h sin α from A along the inclineDa distance 8h sin α from A along the incline
A ball starts falling with zero initial velocity on a smooth inclined plane forming an angle α with the horizontal. Having fallen the distance h, the ball rebounds elastically off the inclined plane. At what distance from the impact point will the ball rebound for the second time?
View SolutionAn inclined plane makes an angle θ0=30∘ with the horizontal. A particle is projected from this plane with a speed of 5ms−1 at an angle of elevation β=30∘ with the horizontal as shown in (Fig. 5.53).
(a) Find the range of the particle on the plane when it strikes the plane.
(b) Find the range of the particle for β=120∘.
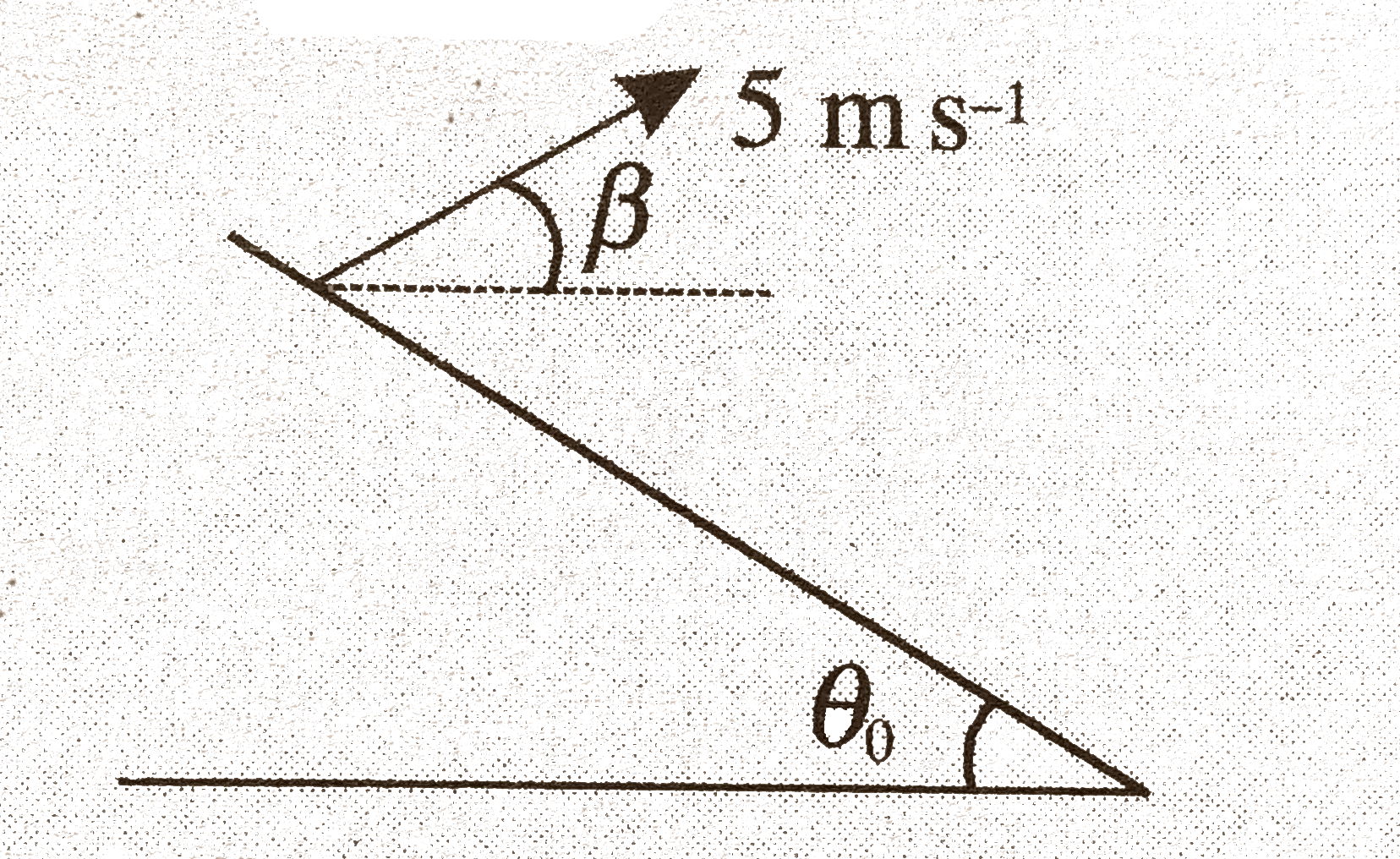 .View Solution
.View SolutionHailstones falling vertically with a speed of 10ms−1, hit the wind screen (wind screen makes an angle 30∘ with the horizontal) of a moving car and rebound elastically. Find the velocity of the car if the driver finds the hailstones rebound vertically after striking.
 .View Solution
.View SolutionA particle is thrown horizontally from a tower of height 20m. If the speed of projection is 20ms then the distance of point from the tower,where the particle hit the ground is:-
View SolutionA particle falls from a height h upon a fixed horizontal plane and rebounds. If e is the coefficient of restitution, the total distance travelled before rebounding has stopped is :
View Solution

