A particle in projected with velocity √3gL at point A (lowest point of the circle) in the vertical plane. Find the maximum height about horizontal level of point A if the string slacks at the point B as shown in figure.

As tension at B, T=0
∴mgcosθ=mv2BL∴vB=√gLcosθ (i)
Now by equation of energy between A and B.
0+12m3gL=12mv2B+mgL(1+cosθ) (ii)
From Eqs. (i) and (ii), cosθ=13
Therefore, height attended by particle after point B where the string slacks is
h′=v2Bsin2θ2g=gLcosθ(1−cos2θ)2g=4L27
Therefore, maximum height about point A is given by.
Hmax=L+Lcosθ+h′=L+L3+4L27=40L27
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.515videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective23videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.326videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
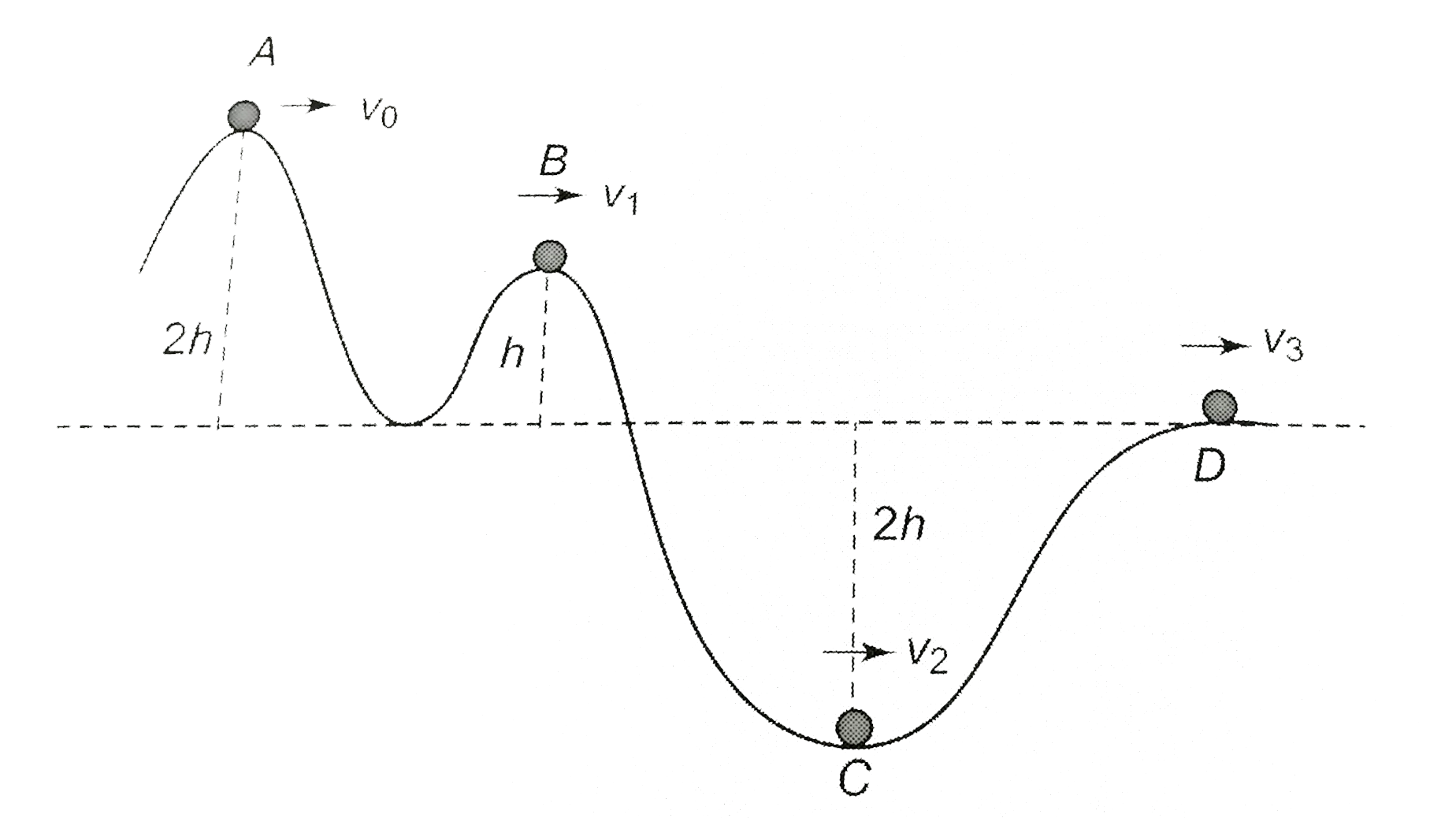
A particle is given velocity v0 at point A as shown in the figure. Find the speed of particle at point B,C and DView SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View Solution
Knowledge Check
- Question 1 - Select One
A particle tied to a string describes a vertical circular motion of radius r continually. If it has a velocity √3gr at the highest point, then the ratio of the respective tensions in the string holding it at the highest and lowest points is
A1:6B1:4C1:3D1:2 - Question 2 - Select One or More
A particle is projected vertically upward with velocity u from a point A, when it returns to the point of projection .
AIts average speed is u/2.BIts average velocity is zero.CIts displacement is zero.DIts average speed is u. - Question 3 - Select One
A particle of mass m is projected with an initial velocity U at an angle θ to the horizontal. The torque of gravity on projectile at maximum height about the point of projection is
AmU2Sin2θ2BmU2Sin2θCmU2Sinθ2D12mU2(Sin2θ)2
A particle of mass m is projected with velocity v at an angle θ with the horizontal. Find its angular momentum about the point of projection when it is at the highest point of its trajectory.
View SolutionA particle is projected under gravity with velocity √2ag from a point at a height h above the level plane at an angle θ to it. The maximum range R on the grond is :
View SolutionA partricle of mass m is projected with a velocity v at an angle of 60∘ with horizontal When the particle is at the maximum height. The magnitude ofits angular momentum about the point ofprojection is
View SolutionA particle is projected from a point A with velocity u√2 at an angle of 45∘ with horizontal as shown in the figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is
 View Solution
View SolutionA particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
View Solution

