A particle is dropped from rest from the top of a building of height 100m. At the same instant another particle is projected upward from the bottom of the building What should be the speed of projection of the particle projected from the bottom of building so that the particle cross each other after 1s? Acceleration due to gravity is 10 m/s2.
100m/s
95m/s
90m/s
105m/s
The correct Answer is:a
To solve the problem of two particles moving towards each other, we will follow these steps:
Step 1: Understand the Problem
We have two particles:
- Particle A is dropped from the top of a building of height 100 m.
- Particle B is projected upwards from the bottom of the building.
We need to find the speed of projection of Particle B such that both particles cross each other after 1 second.
Step 2: Identify the Given Data
- Height of the building (h) = 100 m
- Time until they cross each other (t) = 1 s
- Acceleration due to gravity (g) = 10 m/s²
Step 3: Calculate the Position of Particle A after 1 second
Since Particle A is dropped from rest, we can use the second equation of motion:
s=ut+12gt2
Where:
- s = displacement
- u = initial velocity (0 m/s, since it is dropped)
- g = acceleration due to gravity (10 m/s²)
- t = time (1 s)
Substituting the values:
sA=0⋅1+12⋅10⋅(1)2
sA=0+12⋅10⋅1=5 m
So, after 1 second, Particle A has fallen 5 m from the top of the building.
Step 4: Calculate the Position of Particle B after 1 second
Let the speed of projection of Particle B be u. The distance covered by Particle B in 1 second can also be calculated using the second equation of motion:
sB=ut−12gt2
Substituting the values:
sB=u⋅1−12⋅10⋅(1)2
sB=u−5 m
Step 5: Set Up the Equation for Crossing
For the two particles to cross each other, the sum of the distances they travel must equal the height of the building:
sA+sB=100 m
Substituting the expressions for sA and sB:
5+(u−5)=100
Simplifying the equation:
u=100
Step 6: Conclusion
The speed of projection of Particle B should be 100 m/s for the two particles to cross each other after 1 second.
---
We have two particles:
- Particle A is dropped from the top of a building of height 100 m.
- Particle B is projected upwards from the bottom of the building.
- Height of the building (h) = 100 m
- Time until they cross each other (t) = 1 s
- Acceleration due to gravity (g) = 10 m/s²
Since Particle A is dropped from rest, we can use the second equation of motion:
s=ut+12gt2
Where:
- s = displacement
- u = initial velocity (0 m/s, since it is dropped)
- g = acceleration due to gravity (10 m/s²)
- t = time (1 s)
sA=0⋅1+12⋅10⋅(1)2
sA=0+12⋅10⋅1=5 m
Let the speed of projection of Particle B be u. The distance covered by Particle B in 1 second can also be calculated using the second equation of motion:
sB=ut−12gt2
Substituting the values:
sB=u⋅1−12⋅10⋅(1)2
sB=u−5 m
For the two particles to cross each other, the sum of the distances they travel must equal the height of the building:
sA+sB=100 m
Substituting the expressions for sA and sB:
5+(u−5)=100
Simplifying the equation:
u=100
The speed of projection of Particle B should be 100 m/s for the two particles to cross each other after 1 second.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE ( B.(MULTIPLE CHOICE QUESTIONS))
74 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE ( C.(MULTIPLE CHOICE QUESTIONS))
13 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - REVISION EXERCISE (NUMERICAL PROBLEMS )
7 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)
12 Videos
Similar Questions
A ball A is dropped from the top of a tower 500m high and at the same instant another ball b is projected upwards with the velocity of 100m/s. after how much time and where the two balls will meet?
View SolutionThere is one tower of height h. one particle A is projected upward from top of the tower with a speed u1 at time t=0 . At time t=t0 another particle B is projected upward from the bottom of the tower with a speed u2. When will the particles cross each other?
View Solution
Knowledge Check
A ball is dropped from the top of a building of height 80 m. At same instant another ball is thrown upwards with speed 50 m/s from the bottom of the building. The time at which balls will meet is
A1.6 sB5 sC8 sD10 sA ball is dropped from the top of a building 100 m high. At the same instant another ball is thrown upwards with a velocity of 40ms−1 form the bottom of the building. The two balls will meet after.
A5 sB2.5 sC2 sD3 sA body projected upwards from the top of a builing is an example of ______
Auniform motionBnon-uniform motionCperiodic motionDoscillatory motion
A particle is projected up with initial speed u=10ms−1 from the top of a building at time t=0. At time t=5s the particle strikes the ground. Find the height of the building in meter.
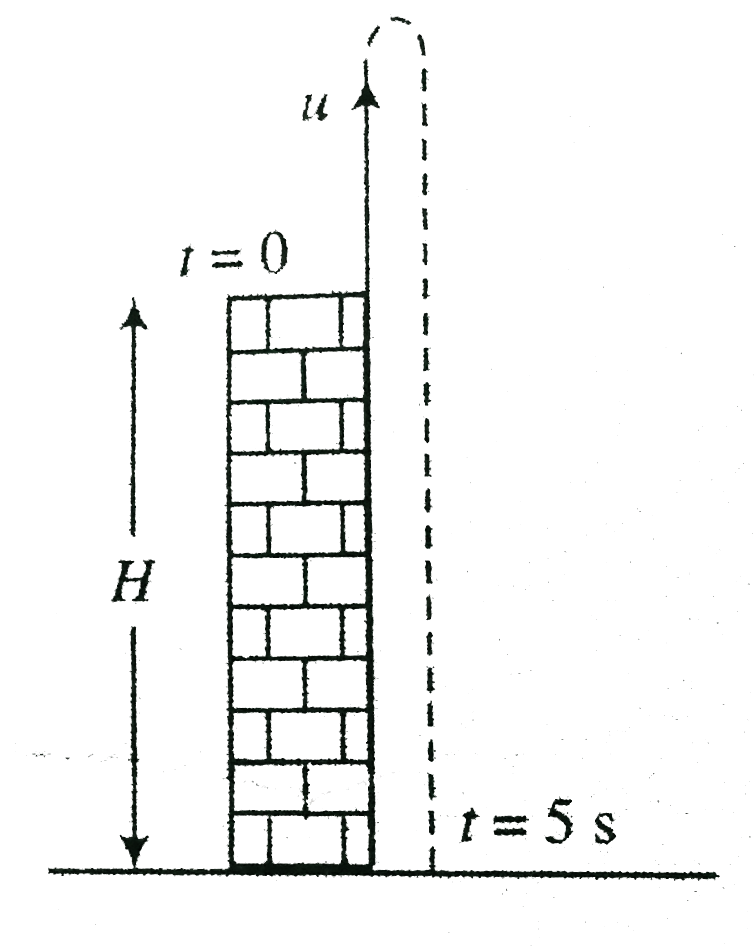 .
.
View SolutionA particle is dropped from a height h and at the same instant another particle is projected vertically up from the ground. They meet when the upper one has descended a height h/3. Find the ratio of their velocities at this instant.
View SolutionA particle is dropped from the top of a high building 360 m. The distance travelled by the particle in ninth second is (g=10m/s2)
View SolutionA stone is dropped from the top of building and at the same time a second stone is thrown vertically upward from the bottom of the building with a speed of 20 ms−1. They pass each other 3 seconds later. Find the height of the building
View SolutionA stone is dropped from the top of a 400m high tower. At the same time another stone is projected vertically upwards from the ground with a speed of 50m/s. The two stones will cross each other after a time
View Solution
