A particle is initially at point A(2,4,6)m moves finally to the pointB(3,2,−3)m. Write the initial position vector,final position,and displacement vector of the particle.
To solve the problem, we need to find the initial position vector, final position vector, and the displacement vector of a particle moving from point A to point B. Let's break it down step by step.
Step 1: Identify the Initial Position Vector
The initial position of the particle is given by point A, which has coordinates A(2,4,6)m.
The position vector →A can be expressed in terms of its coordinates as:
→A=2^i+4^j+6^k
Step 2: Identify the Final Position Vector
The final position of the particle is given by point B, which has coordinates B(3,2,−3)m.
The position vector →B can be expressed as:
→B=3^i+2^j−3^k
Step 3: Calculate the Displacement Vector
The displacement vector →AB is defined as the difference between the final position vector and the initial position vector:
→AB=→B−→A
Substituting the values we found:
→AB=(3^i+2^j−3^k)−(2^i+4^j+6^k)
Now, we perform the subtraction component-wise:
→AB=(3−2)^i+(2−4)^j+(−3−6)^k
→AB=1^i−2^j−9^k
Final Result
Thus, the initial position vector, final position vector, and displacement vector are:
- Initial Position Vector →A=2^i+4^j+6^k
- Final Position Vector →B=3^i+2^j−3^k
- Displacement Vector →AB=1^i−2^j−9^k
---
The initial position of the particle is given by point A, which has coordinates A(2,4,6)m.
→A=2^i+4^j+6^k
The final position of the particle is given by point B, which has coordinates B(3,2,−3)m.
→B=3^i+2^j−3^k
The displacement vector →AB is defined as the difference between the final position vector and the initial position vector:
→AB=→B−→A
→AB=(3^i+2^j−3^k)−(2^i+4^j+6^k)
→AB=(3−2)^i+(2−4)^j+(−3−6)^k
→AB=1^i−2^j−9^k
Thus, the initial position vector, final position vector, and displacement vector are:
- Initial Position Vector →A=2^i+4^j+6^k
- Final Position Vector →B=3^i+2^j−3^k
- Displacement Vector →AB=1^i−2^j−9^k
Topper's Solved these Questions
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise 3.1
Explore 19 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise 3.2
Explore 13 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:TRAVELLING WAVESExercise:Integer
Explore 9 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Archives (integer)
Explore 4 Videos
Similar Questions
An object moves from position (3,4) to (6,5) in the xy-plane. Find the magnitude and direction of displacement vector of the particle.
View SolutionA particle lies in space at point ( 2,3,4) find the magnitude of its position vector.
View SolutionIf a particle moves from the point A(1,2,3) to the point B(4,6,9), its displacement vector be
View SolutionAn insect crawls from A to B where B is the centre of the rectangular slant face. Find the (a) initial and final position vector of the insect and (b) displacement vector of the insect.
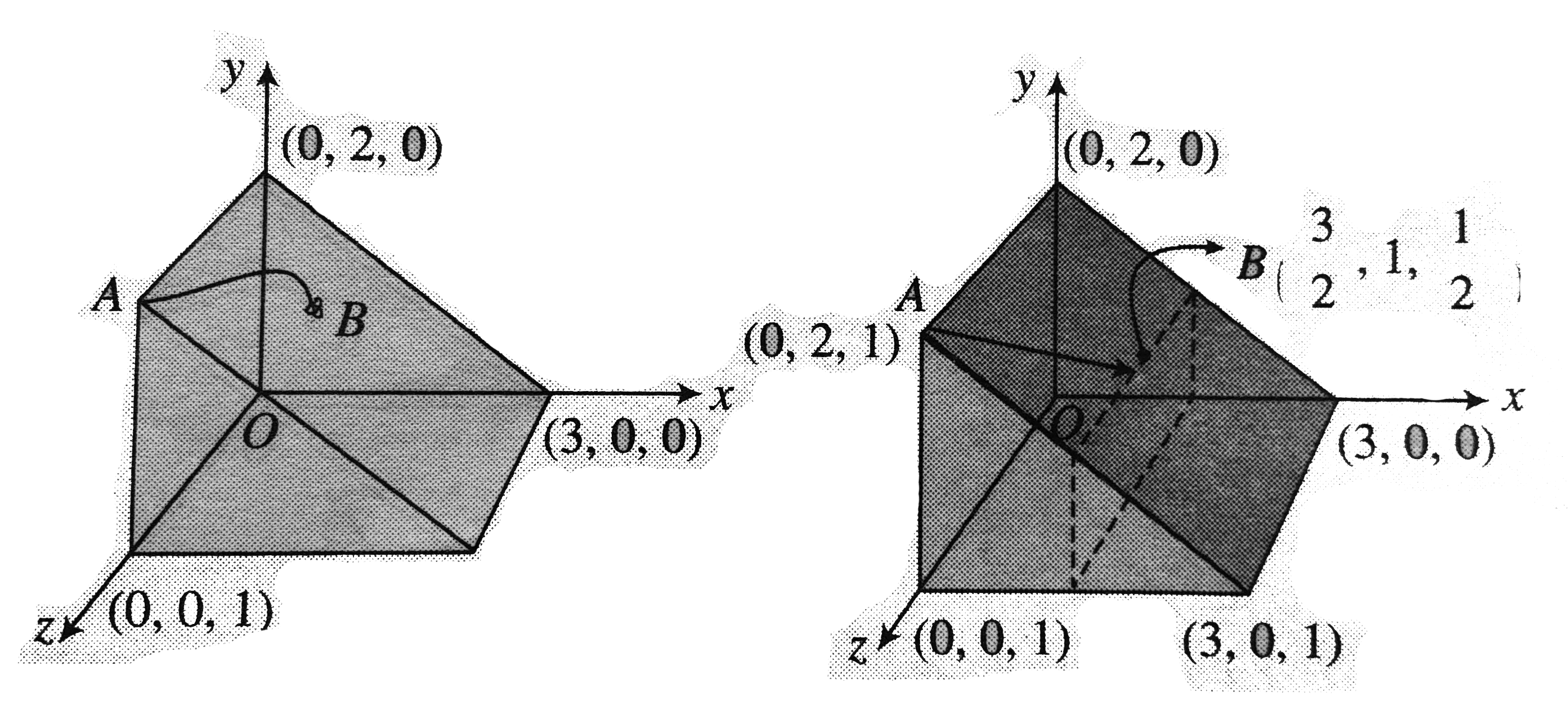 .
.
View SolutionState true or false: Position vector of a point →P is a vector whose initial point is origin.
View SolutionIf the position vector of a point (−4,−3) be →a, find |a| .
View SolutionA particle moves on a straight line with velocity 2 m/s covers a distance of 5 m, returns back to initial position along same path with velocity 4 m/s. The distance and displacement covered by particle are respectively.
View SolutionA particle is moving along x-direction with a constant acceleration a. The particle starts from x=x0 position with initial velocity u. We can define the position of the particle with time by the relation
x=x0+ut+12at2
plot the position of the particle in relation with time is following situations
(i) If initial position of the particle is on negativ x-axis, initial velocity is positive and acceleration is negative.
(ii) If initial position is positive, initial velocity is negative and acceleration is positive.
View SolutionPosition of a particle in a rectangular -co-ordinate (3,2,5). Then its position vector will be
View SolutionPosition of a particle in a rectangular -co-ordinate (3,2,5). Then its position vector will be
View Solution
