A particle is moving eastwards with velocity of 5m/s. In 10sec the velocity changes to 5m/s northwards. The average acceleration in this time is.
1√2m/s2 (North-West)
1√2m/s2 (North-East)
√2m/s2 (North-West)
√2m/s2 (North-East)
The correct Answer is:C
To solve the problem of finding the average acceleration of a particle moving from an eastward velocity to a northward velocity, we can follow these steps:
1. Identify Initial and Final Velocities:
- The initial velocity →Vi is 5m/s eastward. In vector form, this can be represented as:
→Vi=5^im/s
- The final velocity →Vf is 5m/s northward. In vector form, this can be represented as:
→Vf=5^jm/s
2. Calculate Change in Velocity:
- The change in velocity Δ→V is given by:
Δ→V=→Vf−→Vi
- Substituting the values:
Δ→V=5^j−5^i=−5^i+5^j
3. Determine the Time Interval:
- The time interval t is given as 10s.
4. Calculate Average Acceleration:
- The average acceleration →aavg is defined as:
→aavg=Δ→Vt
- Substituting the change in velocity and time:
→aavg=−5^i+5^j10
- This simplifies to:
→aavg=−0.5^i+0.5^jm/s2
5. Calculate the Magnitude of Average Acceleration:
- The magnitude of the average acceleration can be calculated using the Pythagorean theorem:
|→aavg|=√(−0.5)2+(0.5)2=√0.25+0.25=√0.5=1√2m/s2
6. Determine the Direction:
- The average acceleration vector →aavg=−0.5^i+0.5^j indicates that the acceleration is directed towards the northwest.
Final Answer:
The average acceleration of the particle is:
→aavg=1√2m/s2 in the northwest direction.
- The initial velocity →Vi is 5m/s eastward. In vector form, this can be represented as:
→Vi=5^im/s
- The final velocity →Vf is 5m/s northward. In vector form, this can be represented as:
→Vf=5^jm/s
- The change in velocity Δ→V is given by:
Δ→V=→Vf−→Vi
- Substituting the values:
Δ→V=5^j−5^i=−5^i+5^j
- The time interval t is given as 10s.
- The average acceleration →aavg is defined as:
→aavg=Δ→Vt
- Substituting the change in velocity and time:
→aavg=−5^i+5^j10
- This simplifies to:
→aavg=−0.5^i+0.5^jm/s2
- The magnitude of the average acceleration can be calculated using the Pythagorean theorem:
|→aavg|=√(−0.5)2+(0.5)2=√0.25+0.25=√0.5=1√2m/s2
- The average acceleration vector →aavg=−0.5^i+0.5^j indicates that the acceleration is directed towards the northwest.
The average acceleration of the particle is:
→aavg=1√2m/s2 in the northwest direction.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Mathch the columns)
6 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
A particle is moving eastwards with a velocity of 5ms−1. In 10seconds the velocity changes to 5ms−1 northwards. The average acceleration in this time is
View SolutionA particle is moving east wards with a velocity of 15ms−1. In a time of 10 s, the velocity changes to 15ms−1 northwards. Average acceleration during this time is (in ms−2)
View Solution
Knowledge Check
A particle moves in the direction of east for 2s with velocity of 15m/s .Then it moves towards north for 8s with a velocity of 5m/s . The average velocity of the particle is (in m/s)
A1 m/sB5 m/sC7 m/sD10 m/s
A particle is moing with a velocity of 10m/s towards east. After 10s its velocity changes to 10m/s towards north. Its average acceleration is:-
View SolutionA body is moving with velocity 30m/s towards east. After 10s its velocity becomes 40m/s towards north. The average acceleration of the body is.
View SolutionA body is moving with velocity 30m/s towards east. After 10s its velocity becomes 40m/s towards north. The average acceleration of the body is.
View SolutionA car is moving in a circular path of radius 100 m with velocity of 200 m/sec such that in each sec its velocity increases by 100 m/s, the net acceleration of car will be - (in m/sec)
View SolutionThe velocity of an object changes from 50 m/s to 60 m/s in 20 seconds. What is the average acceleration of the object over that interval?
View SolutionA particle is moving eastwards with a speed of 6 m/s. After 6 s, the particle is found to be moving with same speed in a direction 60∘ north of east. The magnitude of average acceleration in this interval of time is
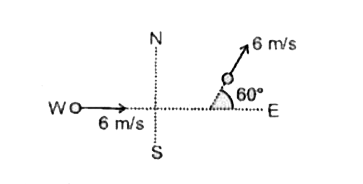
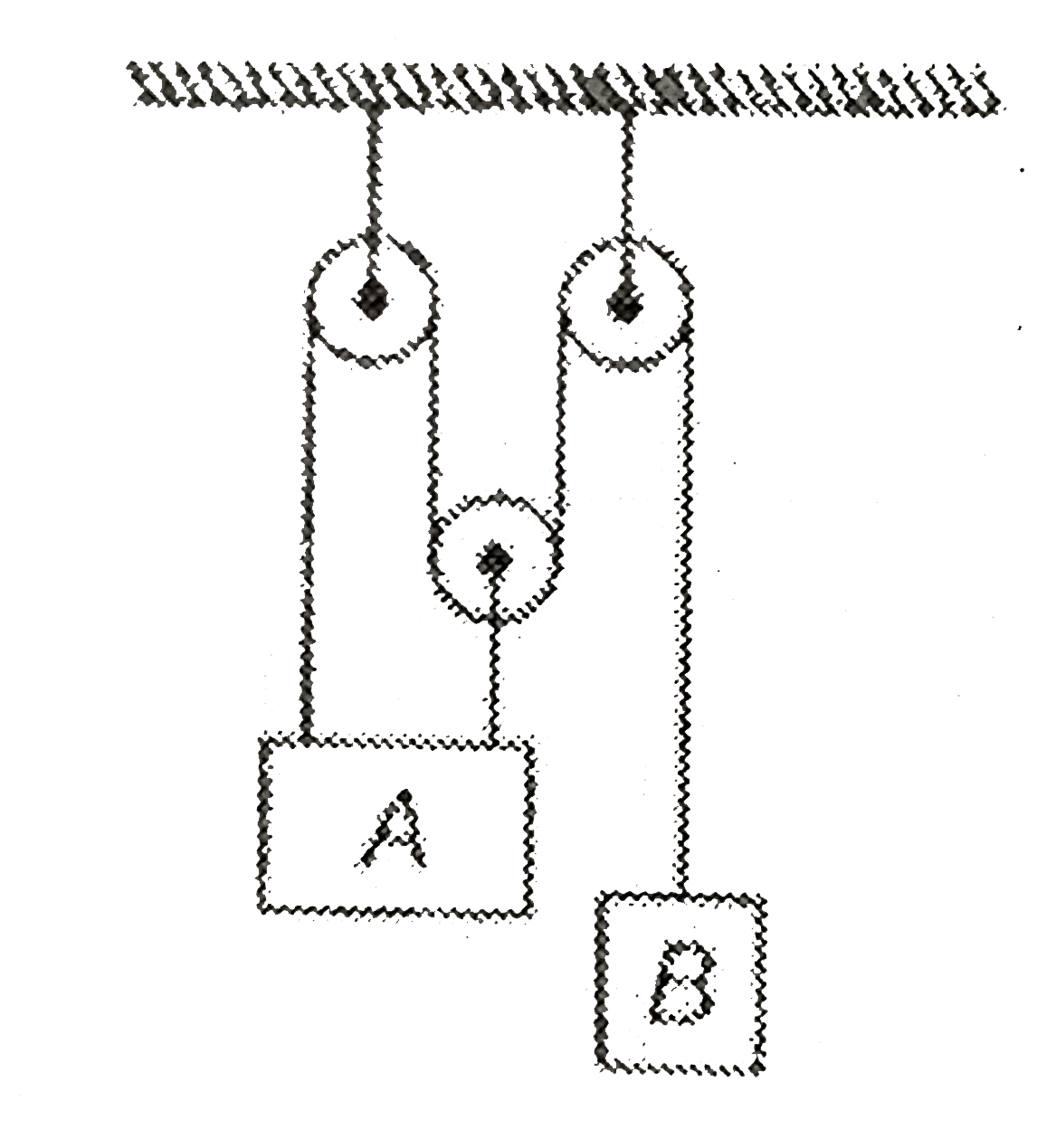
View SolutionAt a given instant. A is moving with velocity of 5m/s upward. What is velocity of B at that time:
View Solution
