A particle is moving in a straight line . Select the correct option (s).
If position and velocity are both negative, then particle moves away from the origin .
If acceleration of the particle is negative , then magnitude of the velocity of particle may increase .
If acceleration of the particle is positive , than magnitude of velocity of particle may decrease .
If velocity of the particle remains zero in a time interval, then acceleration is also zero at any instant during the same time interval .
The correct Answer is:A, B, C, D
To solve the question regarding the motion of a particle in a straight line, we will analyze each option provided and determine whether they are correct or not based on the principles of kinematics.
1. Understanding the Motion:
The question states that a particle is moving in a straight line. We need to analyze the implications of its position, velocity, and acceleration.
2. Analyzing Option 1:
- Statement: "If position and velocity are both negative, then the particle moves away from the origin."
- Explanation: If both position and velocity are negative, the particle is located in the negative direction relative to the origin and is moving further away from it. Thus, this statement is correct.
3. Analyzing Option 2:
- Statement: "If acceleration of the particle is negative, then the magnitude of the velocity of the particle may increase."
- Explanation: Negative acceleration means that the velocity is decreasing if it is positive. However, if the particle is moving in the negative direction (negative velocity), negative acceleration can cause the magnitude of the velocity to increase (e.g., moving from -2v to -v). Therefore, this statement is correct.
4. Analyzing Option 3:
- Statement: "If acceleration of the particle is positive, then the magnitude of the particle may decrease."
- Explanation: Positive acceleration means the velocity is increasing if it is positive. However, if the particle is moving in the negative direction (negative velocity), positive acceleration can cause the magnitude of the velocity to decrease (e.g., moving from -v to 0). Thus, this statement is correct.
5. Analyzing Option 4:
- Statement: "If velocity of the particle remains 0 in a time interval, then acceleration is also 0 at any instant during the same time interval."
- Explanation: If the velocity is zero and does not change during a time interval, the change in velocity (dv) is zero, which implies that acceleration (a = dv/dt) is also zero. Therefore, this statement is correct.
Conclusion:
All four options are correct based on the analysis of the motion of the particle in a straight line.
The question states that a particle is moving in a straight line. We need to analyze the implications of its position, velocity, and acceleration.
- Statement: "If position and velocity are both negative, then the particle moves away from the origin."
- Explanation: If both position and velocity are negative, the particle is located in the negative direction relative to the origin and is moving further away from it. Thus, this statement is correct.
- Statement: "If acceleration of the particle is negative, then the magnitude of the velocity of the particle may increase."
- Explanation: Negative acceleration means that the velocity is decreasing if it is positive. However, if the particle is moving in the negative direction (negative velocity), negative acceleration can cause the magnitude of the velocity to increase (e.g., moving from -2v to -v). Therefore, this statement is correct.
- Statement: "If acceleration of the particle is positive, then the magnitude of the particle may decrease."
- Explanation: Positive acceleration means the velocity is increasing if it is positive. However, if the particle is moving in the negative direction (negative velocity), positive acceleration can cause the magnitude of the velocity to decrease (e.g., moving from -v to 0). Thus, this statement is correct.
- Statement: "If velocity of the particle remains 0 in a time interval, then acceleration is also 0 at any instant during the same time interval."
- Explanation: If the velocity is zero and does not change during a time interval, the change in velocity (dv) is zero, which implies that acceleration (a = dv/dt) is also zero. Therefore, this statement is correct.
All four options are correct based on the analysis of the motion of the particle in a straight line.
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - COMPETITION FILE OBJECTIVE TYPE QUESTIONS (D. MULTIPLE CHOICE QUESTIONS)
9 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - COMPETITION FILE OBJECTIVE TYPE QUESTIONS (Assertion Reason Type Questions)
10 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - COMPETITION FILE OBJECTIVE TYPE QUESTIONS (JEE (Advanced) for IIT Entrance)
2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
A particle is moving in a straight line and its velocity varies with its displacement as v=√4+4s m/s. Assume s=0 at t=0. find the displacement of the particle in metres at t=1s.
View SolutionA particle is moving in a straight line its speed depends on x as shown. The acceleration of particle is...
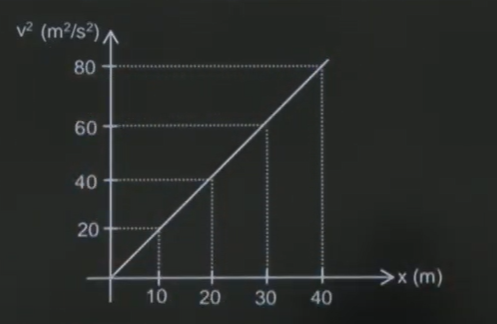
View Solution
Knowledge Check
A particle is moving along a straight line.
AIf the acceleration of the particle is more than that of another object, the particle is moving faster.BIf the acceleration is positive, the speed must be increasing.CIf the acceleration and the velocity have the same sign, the speed must be increasing.DIf the acceleration is zero, the velocity is constant but the speed may be changing.For a particle moving in a straight line
AIf velocity is negative and acceleration is positive then speed increases.Bif velocity is positive and acceleration is negative then speed decreases.Cif velocity is zero at an instant then acceleration must also be zero at that instant.Dit is possible that speed of a particle is never zero in an interval of time, but average speed is zero.Select correct option(s) :
A B
B C
C D
D
Select correct option (s) :
View SolutionSelect correct option (s).
View SolutionSelect correct option(s):
View SolutionThe figure shows velocity-time graph of a particle moving along a straight line. Identify the correct statement.
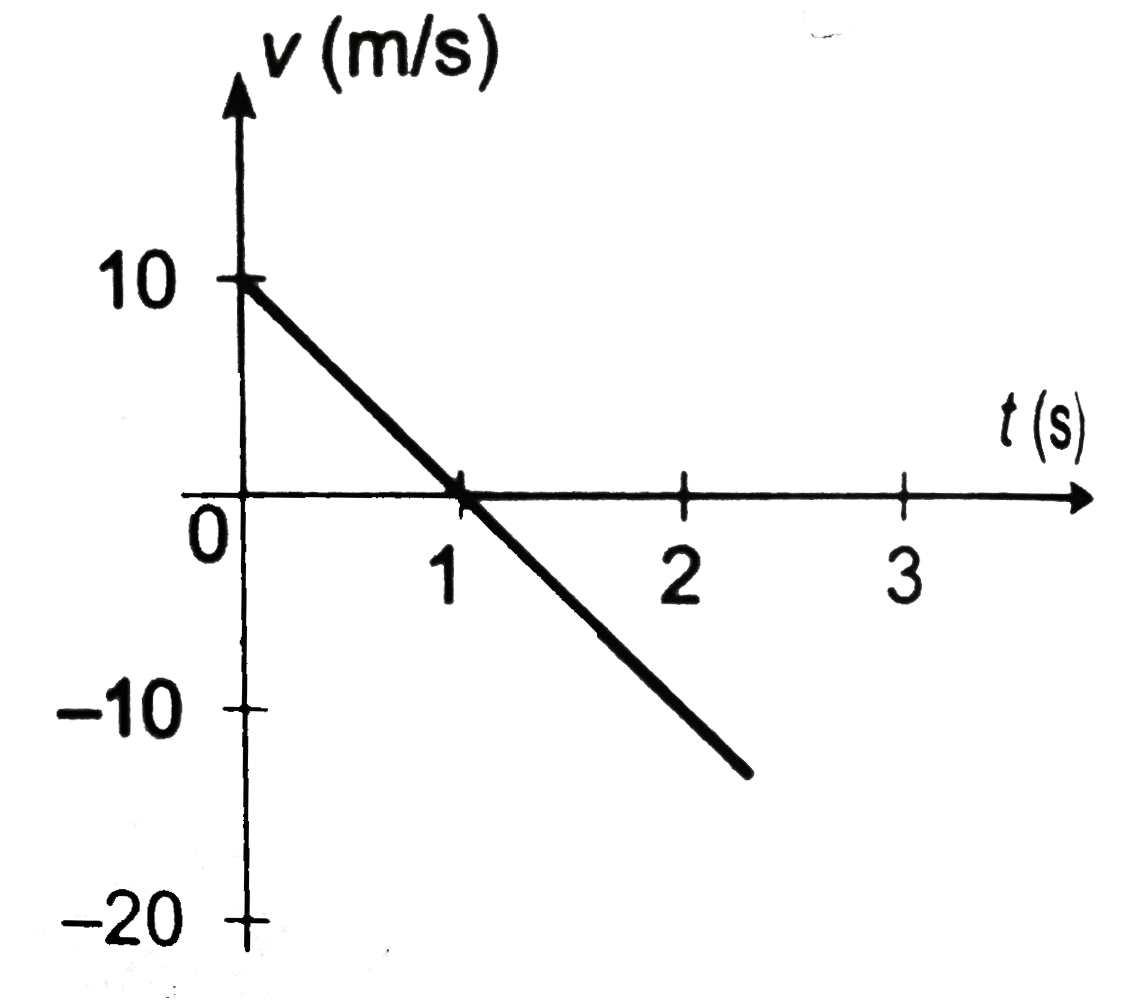
View SolutionA particle is moving on a straight line with constant retardation of 1m/s2. Its initial velocity is 10m/s.
View Solution
