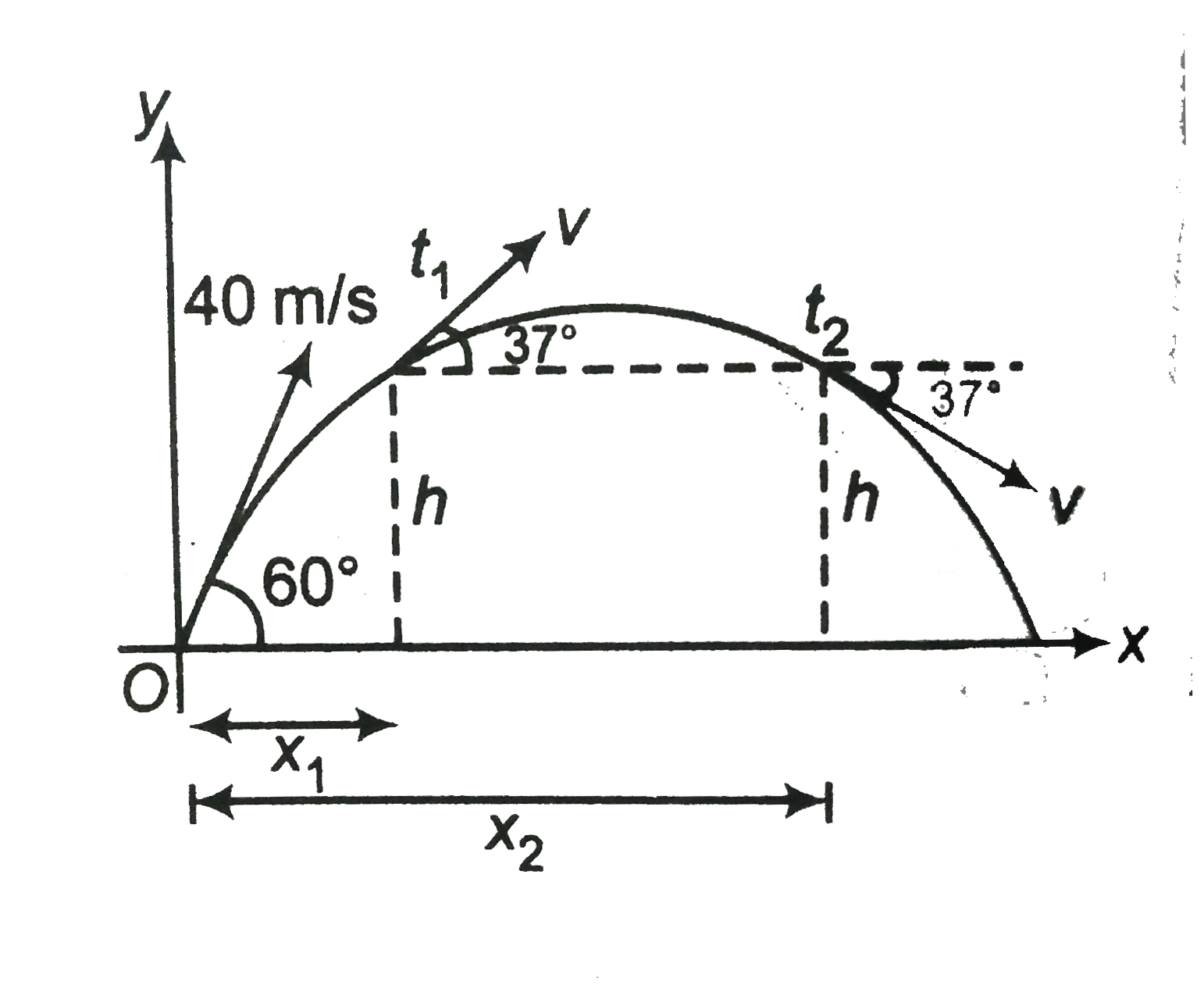
A particle is projected from ground with velocity 40m/s at 60∘ from horizontal.
(a) Find the speed when velocity of the particle makes an angle of 37∘ from horizontal.
(b) Find the time for the above situation.
(C ) Find the vertical height and horizontal distance of the particle from the starting point in the above position. Take g=10m/s2 .
The correct Answer is:A
In the figure shown,
ux=40cos60∘=20m/s
uy=40sin60∘=20√3m/s
ax=0anday=−10m/s2
(a) Horizontal component of velocity remains unchanged.
vx=ux
or vcos37∘=20
⇒v(0.8)=20
∴v=25m/s.
(b) Using, vy=uy+ayt⇒t=vy−uyay
Fort1,t1=vsin37∘−20√3−10=(25)(0.6)−20√3−10=1.96s
Fort2,t2−vsin37∘−20√3−10=−(25)(0.6)−20√3−10=4.96s
(c) Vertical height h=sy
Let us calculate at t1
∴h=uyt1+12ayt21=(20√3)(1.96)+12(−10)(1.96)2
=48.7 m.
Horizontal distance
x1=uxt1
= (20)(1.96) = 39.2m
Similarly, x2=uxt2=(20)(4.96)
=99.2 m.
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 2
1 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 3
4 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
A particle is projected from ground with velocity 50m/s at 37∘ from horizontal. Find velocity and displacement after 2 s. sin37∘=35.
View SolutionA particle is projected from ground with velocity 40(√2)m/sat45∘. Find
(a) velocity and
(b) displacement of the particle after 2 s. (g=10m/s2)
View Solution
Knowledge Check
A particle is projected with velocity 50 m/s at an angle 60∘ with the horizontal from the ground. The time after which its velocity will make an angle 45∘ with the horizontal is
A2.5 sB1.83 sC2.37 sD3.72 mA particle is projected from horizontal ground with speed 5ms−1 at 53∘ with horizontal. Find time after which velocity of particle will be 45∘ with horizontal:
A110 secB310 secC510 secD710 secA particle is projected from horizontal XZ plane with velocity (uxˆi+uyˆi+uzˆk) from origin (+ yaxis is upward). Find time when velocity of particle will be at 37∘ with horizontal.
Auy√u2x+u2zgB3uy−4√u2x+u2z3gC3uy+4√u2x+u2z3gDuy+√u2x+u2z3g
A particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionIf a particle is projected with a velocity 49m/s making an angle 60∘ with the horizontal, its time of flight is
View SolutionIf a particle is projected with a velocity 49m/s making an angle 60∘ with the horizontal, its time of flight is
View SolutionA particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View SolutionA particle is projected from horizontal making an angle of 53∘ with initial velocity 100ms−1. The time taken by the particle to make angle 45∘ from horizontal is
View Solution
