A particle is projected from point O on the ground with velocity at angle . It strikes at a point C on a fixed smooth plane AB having inclination of with horizontal as shown in figure. If the particle does not rebound, calculate.
(a) coordinates of point C in reference to coordinate system as shown in the figure.
(b) maximum height from the ground to which the particles rises.

The correct Answer is:A, B, D
(a) Let, (x,y) be the coordinates of point C.

………(i)
As point C lies on the trajectory of a parabola,
we have
.........(ii)
Given that ,
Solving Eqs. (i) and (ii), we get x = 5m and y = 1.25m.
Hence, the coordinates of point C are (5m, 1.25m).
(b) Let be the vertical component of velocity of
the particle just before collision at C.

Using
Thus, at C, the particle has only horizontal
component of velocity
Given, that the particle does not rebound after collision. So, the normal component of velocity
(normal to the plane AB) becomes zero. Now,
the particle slides up the plane due to tangential
component
Let h be the further height raised by the particle.
Then,
Height of the particle from the ground
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 More Than One Correct
8 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
A ball is projected from the point O with velocity 20 m/s at an angle of 60∘ with horizontal as shown in figure. At highest point of its trajectory it strikes a smooth plane of inclination 30∘ at point A. The collision is perfectly inelastic. The maximum height from the ground attained by the ball is (g=10m/s2)

View Solution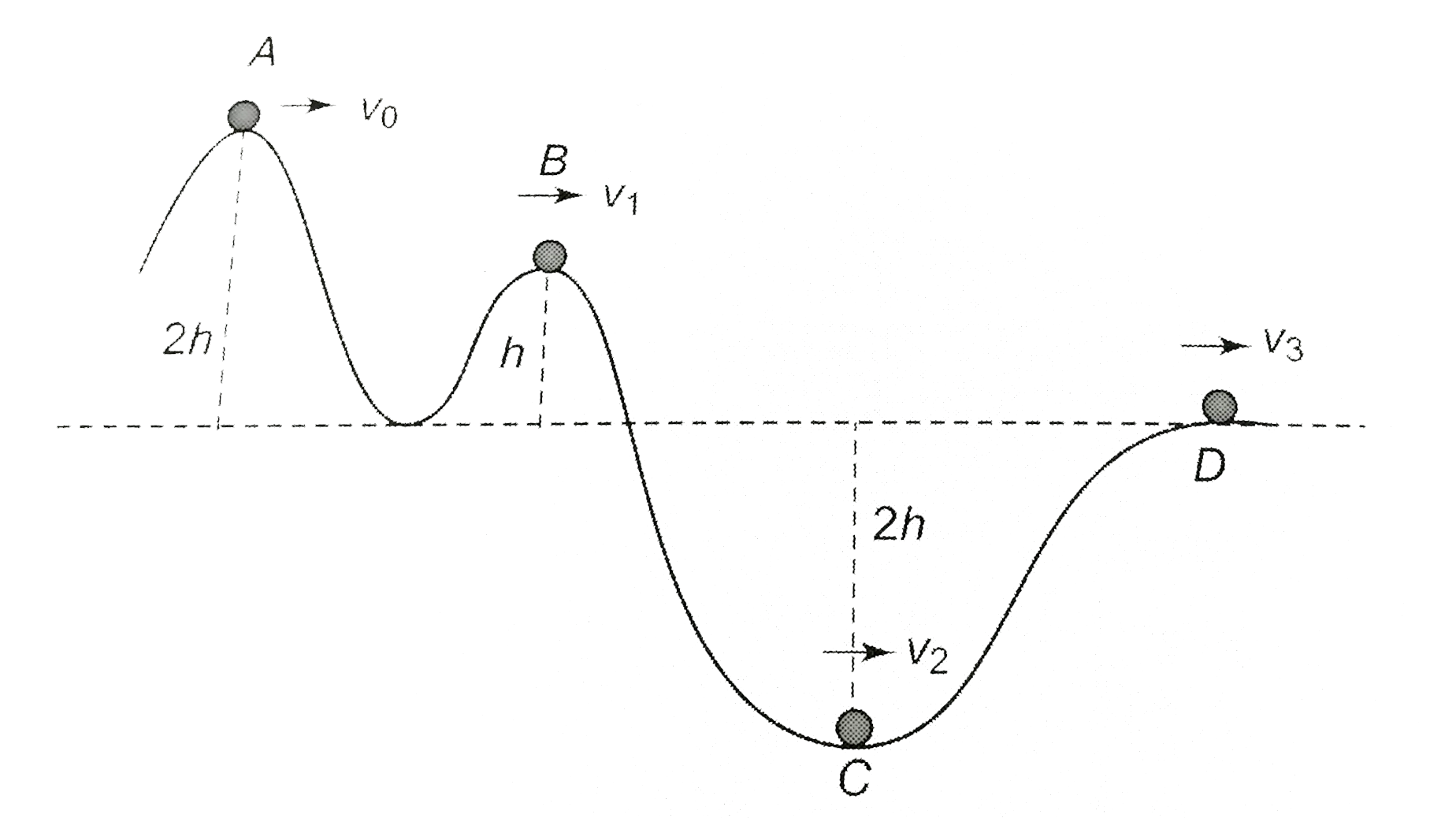
A particle is given velocity v0 at point A as shown in the figure. Find the speed of particle at point B,C and D
View Solution
Knowledge Check
A particle is project d from point A with velocity u at an angle α with horizontal. In its parabolic path, at point P the particle is moving at right angles to its initial direction of projection. Its velocity at P is:
AutanαBucotαCucosαDucosecαA particle is projected from a point A with velocity √2u an angle of 45∘ with horizontal as shown in figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is
 A√3u2Bu2C2u√3Du
A√3u2Bu2C2u√3DuA particle is projected from a point A with velocity u√2 at an angle of 45∘ with horizontal as shown in the figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is
 A√3u2Bu2C2u√3DNone
A√3u2Bu2C2u√3DNone
A particle is projected along an inclined plane as shown in figure. What is the speed of the particle when it collides at point A ? (g=10m/s)

View SolutionA particle is thrown at an angle with horizontal from the ground. After 4s it reaches to a point P and after 5 more seconds it strikes the ground. Find the height of P the maximum height attained by the particle.
View SolutionA projectile is projected on an inclined plane as shown in figure. 'D' is a point of maximum height from inclined plane then :

View SolutionA ball thrown down the incline strikes at a point on the incline 25m below the horizontal as shown in the figure. If the ball rises to a maximum height of 20m above the point of projection, the angle of projection α (with horizontal x axis) is
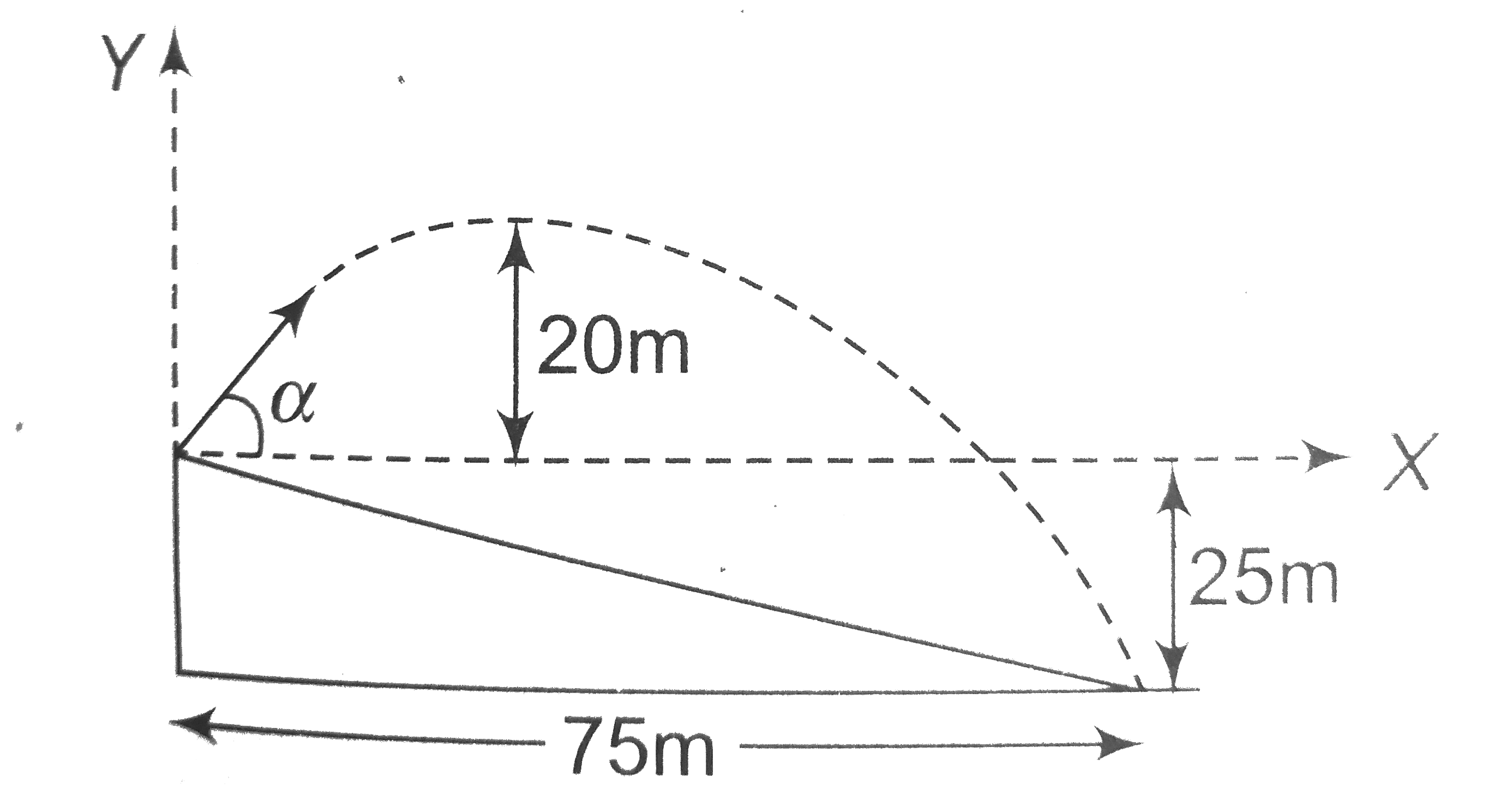
View Solution
A particle is projected from point A on plane AB, so that AB=2u2tanθg√3 in the figure as shown. If u is the velocity of projection, find angle θ.
View Solution
