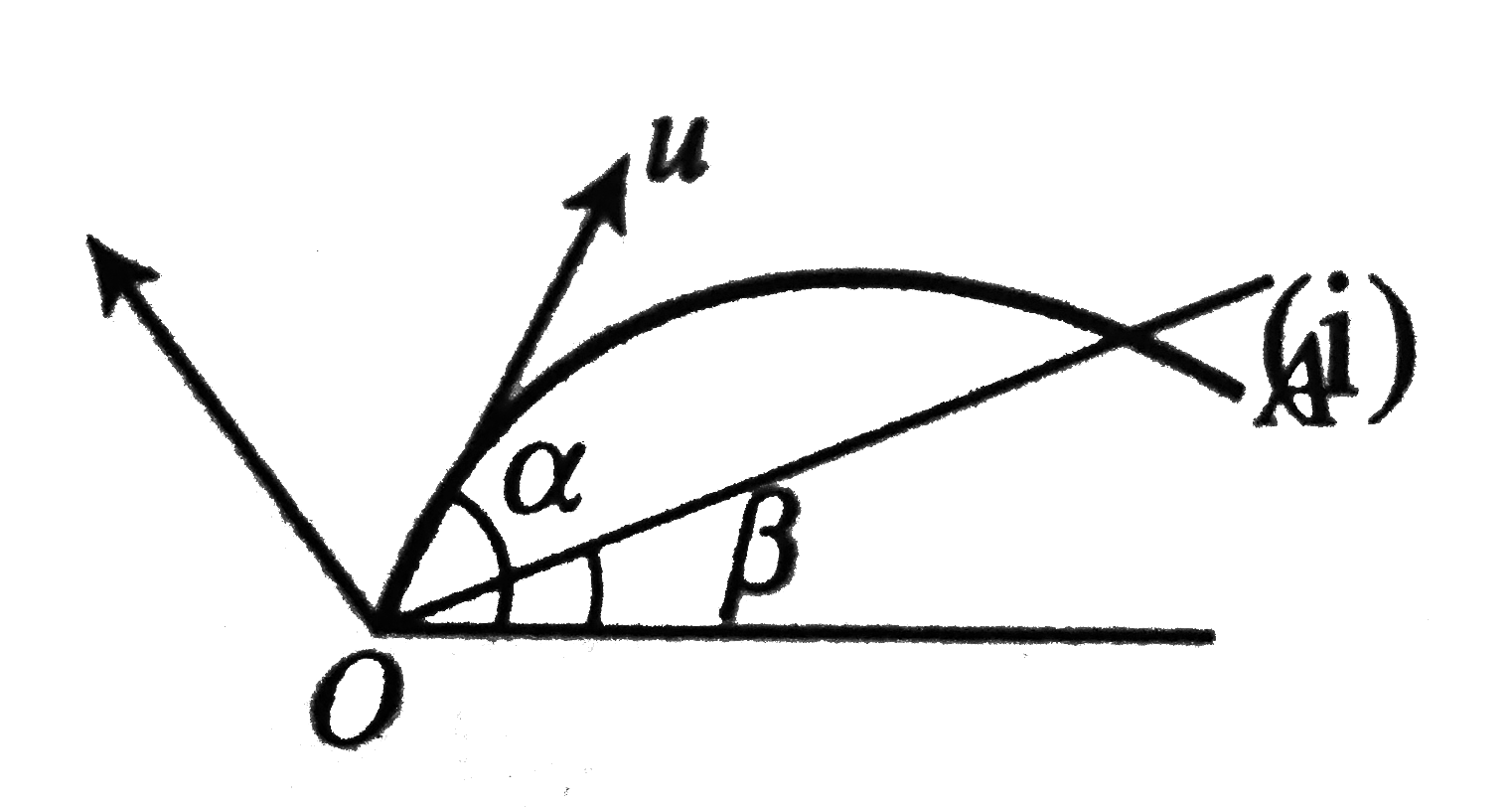
A particle is projected up an inclined plane of inclination β at an elevation ∝ to nthe horizontal. Find the ratio between tan∝andtanβ, if the particle strikes the plane horizontally.
The correct Answer is:2
(a) T=2usin(∝−β)gcosβ
Now we shall consider the motion of particle along OA.
(b) When the particle strikes the plane horizontally
In this case, t=2usin(∝−β)gcosβ
and 0=usin∝−gt
usin∝=g[2usin(∝−β)gcosβ]
2tanβ=tan∝⇒tan∝:tanβ=2.
 .
.
Topper's Solved these Questions
Similar Questions
A particle is projected up an inclined plane of inclination β at na elevation ∝ to the horizon. Show that
(a) tan∝=cotβ+2tanβ, if the particle strikes the plane at right angles
(b) tan∝=2tanβ, if the particle strikes the plane horizontally.View SolutionConsider an object P on an inclined plane of inclination β.
A shot is fired O at an angle α with horizontal. Find the relation between α and β, if the shot hits the object horizontally.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle is projected with a certain velocity at an angle ∝ above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally, then ∝ is equal to.
A30∘+tan−1(√32)B45∘C60∘D30∘+tan−1(2√3)
A particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View SolutionA projectile is thrown at an angle θ with an inclined plane of inclination β as shown in fig. 1E108. Find the relation between β and θ ifv :
(a)projectile strikezs the inclined plane perpendicularly,
(b) projectile strikes the inclined plane horizontal.View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α(from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?
 View Solution
View SolutionA particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
View SolutionA ball is projected from the foot of an inclined plane of inclination 30∘ at an angle 60∘ with the horizontal,with velocity 20√3ms−1 .The time after which the ball will strike the plane is
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
View Solution

