A particle is projected with a speed u at an angle θ to the horizontal. Find the radius of curvature.
At the point where the particle is at a highest half of the maximum height H attained by it.
2u2(1+cos2θ)3/2g2√2cosθ
u2(1+cos2θ)3/2g2√2cosθ
u2(1−sin2θ)3/2g2√2cosθ
u2(1−tan2θ)3/2g2√2cosθ
The correct Answer is:B
(b) We know that ac=v2r⇒r=v2ac, where r is known as radius of curvature. At the highest point, v=ucosθ,
ac=g⇒r=u2cos2θg
Similarly, find the velocity and ac at the given point and then find r.ac will be component of g perpendicular to velocity at that point (Fig. S5.93).
vcos(θ/2)=ucosθ
⇒v=ucosθsec(θ/2)
ac=gcos(θ/2)
Now find r=v2ac
h=H/2,vcosϕ=ucosθ ...(i)
v2sin2ϕ=u2sin2θ−2g(H)2...(ii)
Squaring Eq. (i) and adding in Eq. (ii), we get
v2=u2−gH where H=u2sinθ2g
ac=gcosϕ=gucosθv
Now r=v2ac.
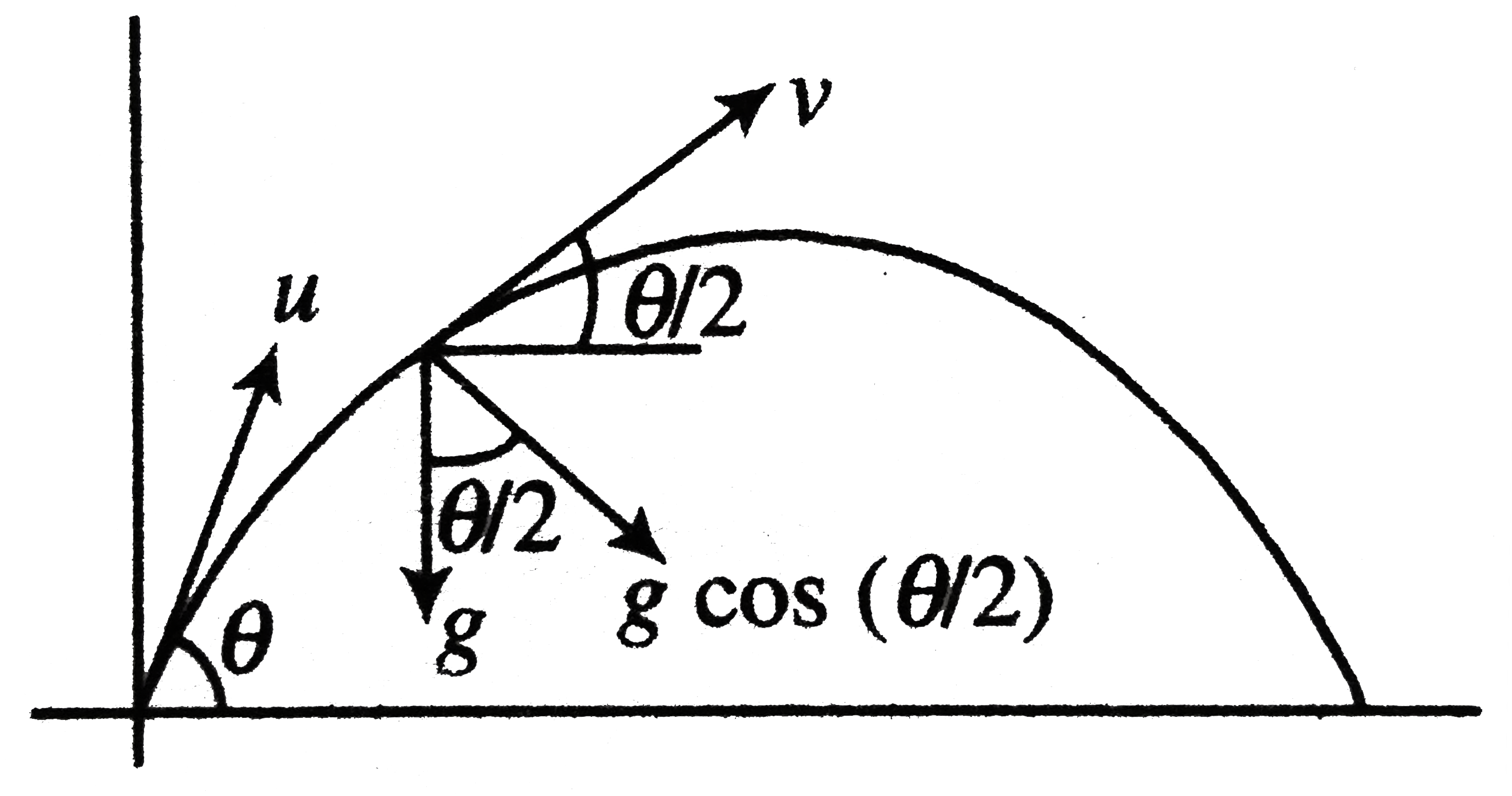 ,
, .
.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer9videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning5videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
A particle is projected with a speed v at an angle θ with the horizontal. Find the mean power delivered by gravity during the ascent of the particle.
View SolutionA particle is thrown with an initial speed v0 at an angle α to the horizontal. Find the radius of curvature r at the highest point of its path, and its ratios to the maximum height H and to the distance L of the particle's flight.
View Solution
Knowledge Check
- Question 1 - Select One
A particle is projected with speed u at angle θ to the horizontal. Find the radius of curvature at highest point of its trajectory
Au2cos2θ2gB√3u2cos2θ2gCu2cos2θgD√3u2cos2θg - Question 2 - Select One
A stone is projected with speed u and angle of projection is θ. Find radius of curvature at t=0.
Au2cos2θgBu2gsinθCu2gcosθDu2sin2θg - Question 3 - Select One
A particle is projected with a speed u at an angle θ with the horizontal. What will be the speed of the particle when direction of motion of particle is at an angle α with the horizontal?
AucosθsecαBusecθcosαCucosθtanαDucosθcotα
A particle is projected with a speed u at an angle 60∘ with the horizontal.What is the radius of curvature of the parabola traced out by the projectile at a point where the particle velocity makes an angle 30∘ with the horizontal?
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA particle is projected with a speed u at an angle θ with the horizontal . If R1 is radius of curvature of trajectory at the initial point and R2 is the radius of curvature at the highest point . Value of R2/(R1 is found to be cosnθ. What is the value of n ?
View SolutionA body is projected with speed u at an angle θ to the horizontal to have maximum range. Its velocity at the highest point will be ___.
View SolutionA particle of mass m is projecte dwilth speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View Solution

