A particle is projected with a speed u at angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circle? This radius is called the adius of curvature of the curve at the point.
u2cos2θ2g
√3u2cos2θ2g
u2cos2θg
(√3u2cos2θ)g
The correct Answer is:C
( c) We know that ac=v2r⇒r=v2ac, where r is known as radius of curvature. At the highest point, v=ucosθ,
ac=g⇒r=u2cos2θg
Similarly, find the velocity and ac at the given point and then find r.ac will be component of g perpendicular to velocity at that point (Fig. S5.93).
vcos(θ/2)=ucosθ
⇒v=ucosθsec(θ/2)
ac=gcos(θ/2)
Now find r=v2ac
h=H/2,vcosϕ=ucosθ ...(i)
v2sin2ϕ=u2sin2θ−2g(H)2...(ii)
Squaring Eq. (i) and adding in Eq. (ii), we get
v2=u2−gH where H=u2sinθ2g
ac=gcosϕ=gucosθv
Now r=v2ac.
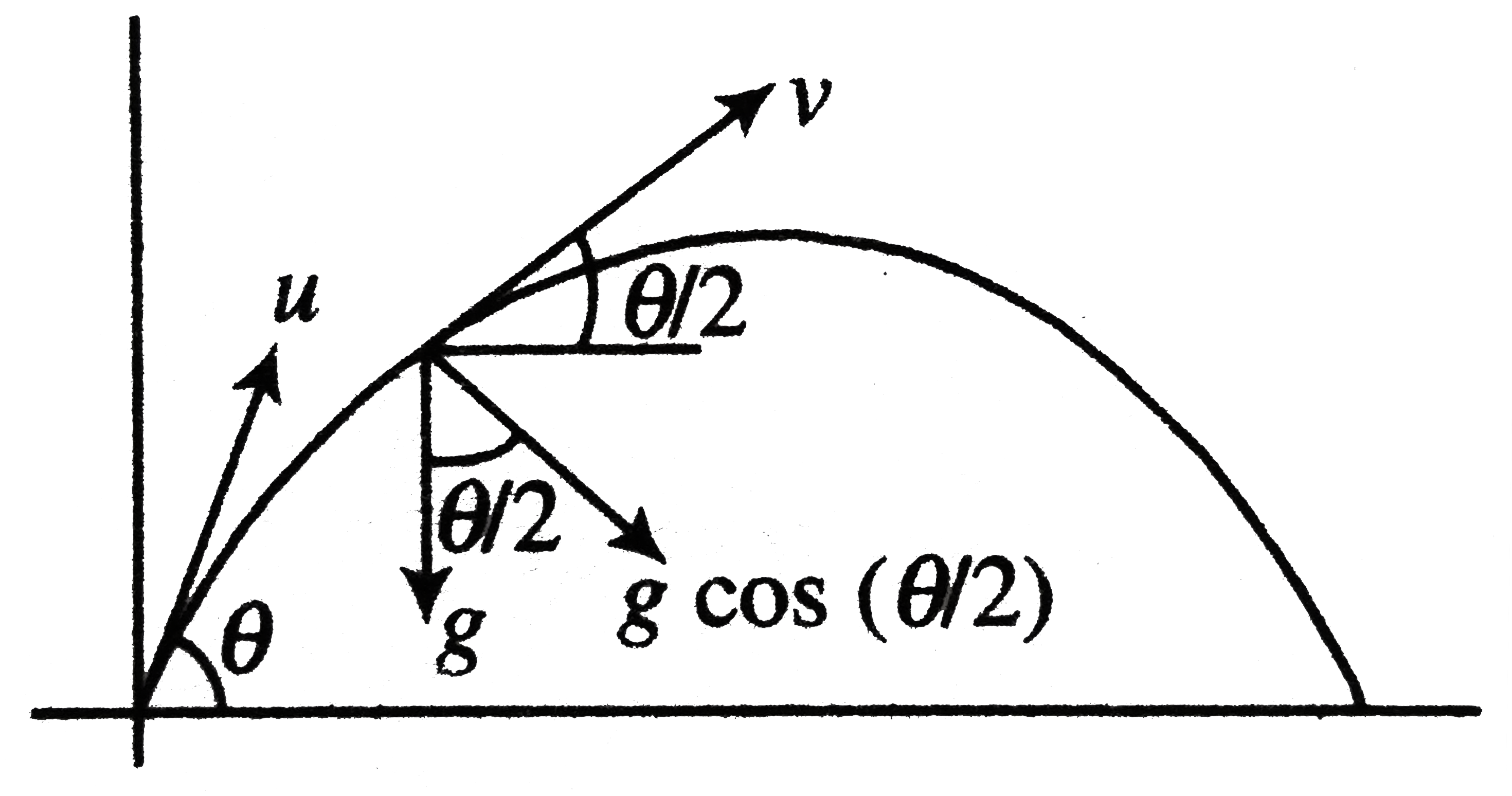 ,
,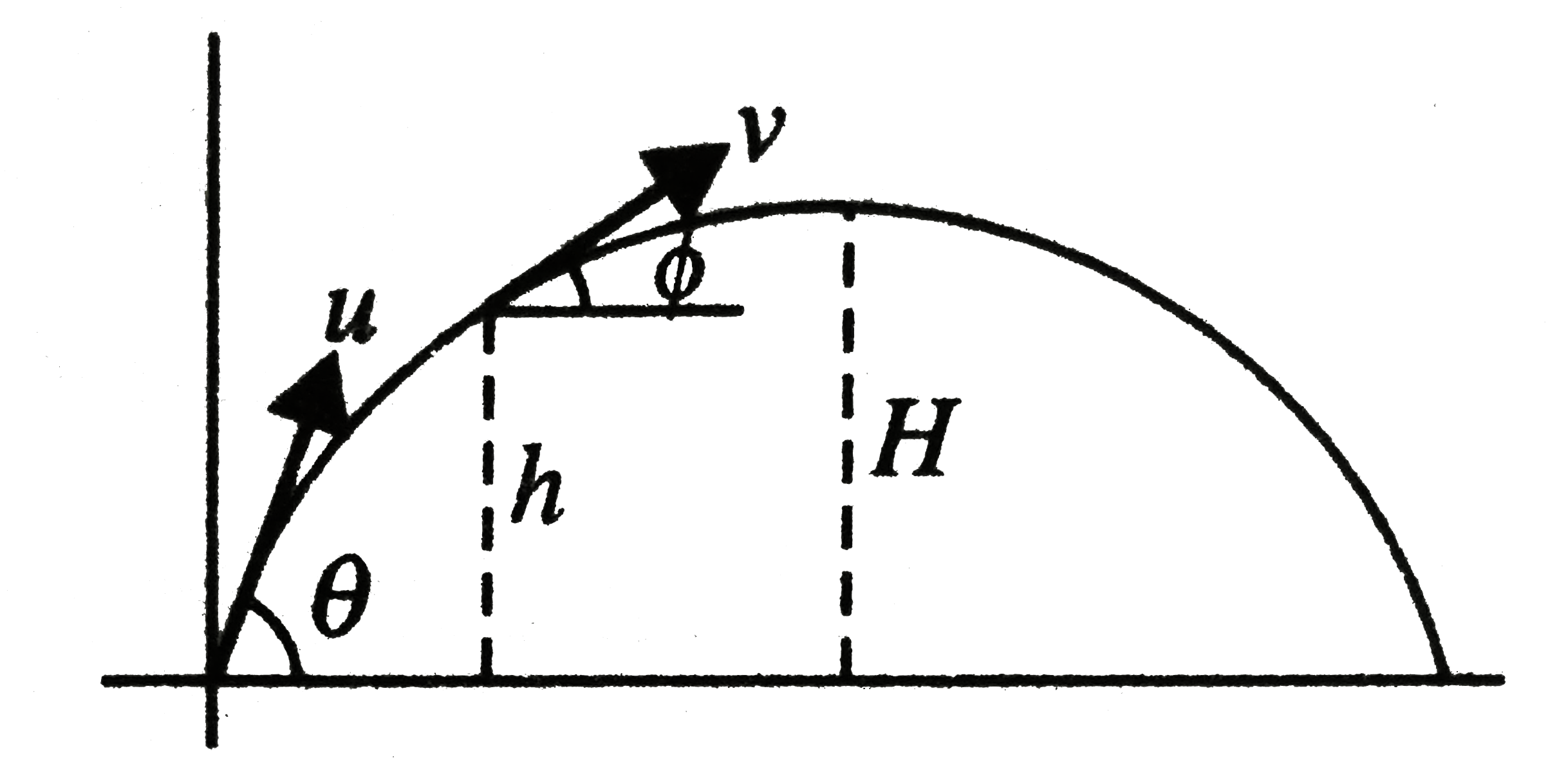 .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning
5 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A particle is projected with a speed u at angle θ with the horizontal. Consider a small part of its path ner the highest position and take it approximately to be a circular arc. What is the rdius of this circle? This radius is called the adius of curvature of the curve at the point.
View SolutionA body is projected with speed u at an angle θ to the horizontal to have maximum range. Its velocity at the highest point will be ___.
View Solution
Knowledge Check
A particle is projected with speed u at angle θ to the horizontal. Find the radius of curvature at highest point of its trajectory
Au2cos2θ2gB√3u2cos2θ2gCu2cos2θgD√3u2cos2θgA particle is fired with velocity u making angle θ with the horizontal.What is the change in velocity when it is at the highest point?
A12μ2sin2θB12μ2cos2θC12μ2D12μ2sin22θA particle is fired with velocity u making angle θ with the horizontal.What is the change in velocity when it is at the highest point?
AucosθBuCusinθD(ucosθ−u)
A body is projected with a speed (u) at an angle to the horizontal to have maximum range. What is its velocity at the highest point ?
View SolutionA particle of mass m is projected with a speed u at an angle θ with the horizontal. Find angular momentum of particle after time t about point of projection.
View SolutionA projectile is projected with a speed u at an angle θ with the horizontal. What is the speed when its direction of motion makes an angle θ/2 with the horizontal
View SolutionA particle is projected with a speed u at an angle θ with the horizontal. What will be the speed of the particle when direction of motion of particle is at an angle α with the horizontal?
View SolutionA particle of mass m is projected at an angle α to the horizontal with an initial velocity u. The work done by gravity during the time it reaches its highest point is
View Solution
