A particle is projected with a velocity of 10√2 m/s at an angle of 45° with the horizontal Find the interval between the moments when speed is √125 m/s
(g=10m/s2),un=10,uy=0
v2=v2x+v2y
125=100+v2y
vy=5Δ=2vyg=2×510=1s
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Vectors & Scalars)
25 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Addition & Subtractions of Vectors)
10 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - ADDITIONAL EXERCISE
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
Similar Questions
A projectile is thrown with a velocity of 10√2ms−1 at an angle of 45° with the horizontal. The time interval between the moments when the speeds are √125ms−1 is (g=10ms−2)
View SolutionA projectile is thrown with a velocity of 10ms−1 at an angle of 60∘ with horizontal. The interval between the moments when speed is √5gm/s is (Take, g=10ms−2)
View SolutionA projectile is thrown with a velocity of 18 m/s at an angle of 60∘ with horizontal. The interval between the moment when speed is 15 m/s is (g=10ms2)
View SolutionA particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
View SolutionA particle is projected from ground with velocity 40√2m/s at 45∘. At time t=2s
View SolutionA particle is projected upwards with a velocity of 100m/s at an angle of 60∘ with the vertical. Find the time when the particle will move perpendicular to its initial direction, taking g=10m/s2.
View SolutionTwo particles A and B are projected simultaneously from two towers of heights 10 m and 20m respectively. Particle A is projected with an initial speed of 10√2m/s at an angle of 45∘ with horizontal, while particle B is projected horizontally with speed 10m/s. If they collide in air, what is the distance d between the towers?
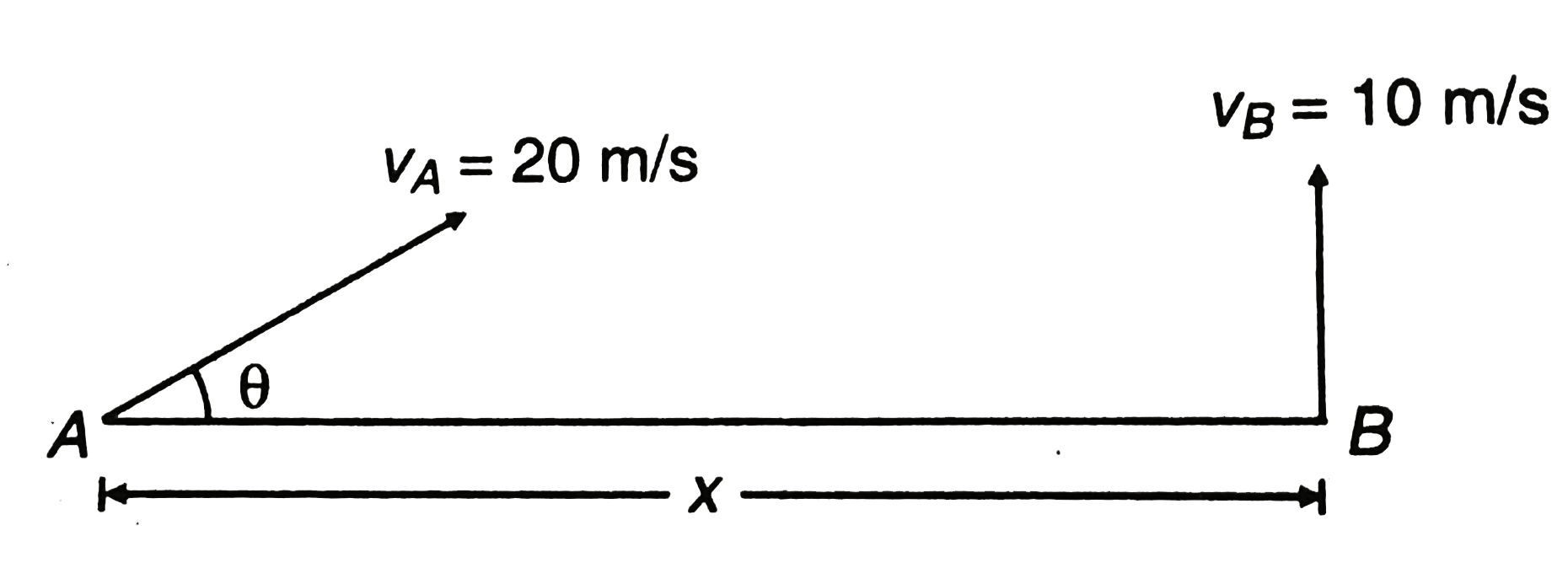
View SolutionA particle is projected with a speed 10√2ms−1 and at an angle 45∘ with the horizontal. The rate of change of speed with respect to time at t=1s is (g=10ms−2)
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA particle A is projected with an initial velocity of 60m/s at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a)the angle of projection α of particle B, (b) time when the collision takes place and (c) the distance of P from A, where collision occurs. (g=10m/s2)
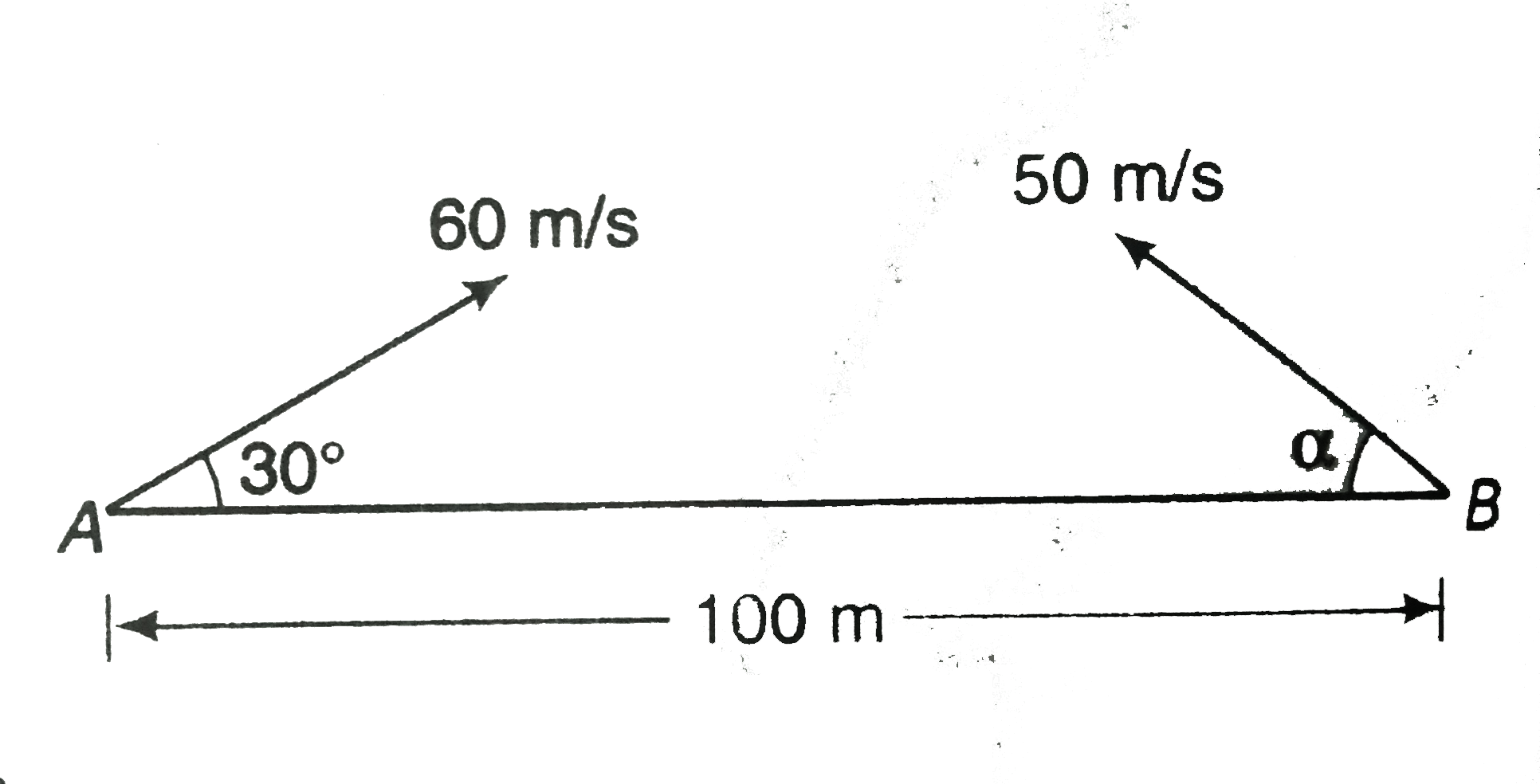
View Solution
