A particle is projected with velocity u at angle $θ$ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.

Video Solution

Text Solution

Verified by Experts

Method 1 : Using properties of projectile motion
As we have to calculate the time between two positions $A and B$ where the final direction of movement is perpendicular to the initial direction of movement. So for our own comfortability, we can choose the initial direction of motion as x - axis. Also let us assume the velocity at position $B$ to be $v$ .
Now analyzing motion in x - and y - direction, we have
$u_{x} = u, u_{y} = 0$
$a_{x} = - g sin θ, a_{y} = - g cos θ$
Here we can the following formula $v = u + a t$ in x - direction.
As we have the values of initial velocity, final velocity, and acceleration we can find $t$ . Therefore,
$v_{x} = u_{x} + a_{x} t$
At position $B, v_{x} = 0$ , as the fianl velocity is equal to the y - component of velocity. Therefore,
$0 = u - g sin θ . t$
Thus, $t = \frac{u}{g sin θ}$ which is the required time to travel.
Method 2 : Using vectors
As $u and v$ both are perpendicular to each other. We can use the orthogonality property of dot product, i.,e., if two vetor are perpendicular to each other their dot product is zero, in order to find out the time of travel to the desired position. So,
so, $\to u . \to v = 0 \Rightarrow \to u . (\to u + \to a t) = 0 \Rightarrow \to u . \to u + \to u . \to a t = 0$
$\Rightarrow u^{2} + u g cos (90^{\circ} + θ) t = 0$
[because angle between $u$ and $g i s 90^{\circ} + θ$ as from (Fig)]

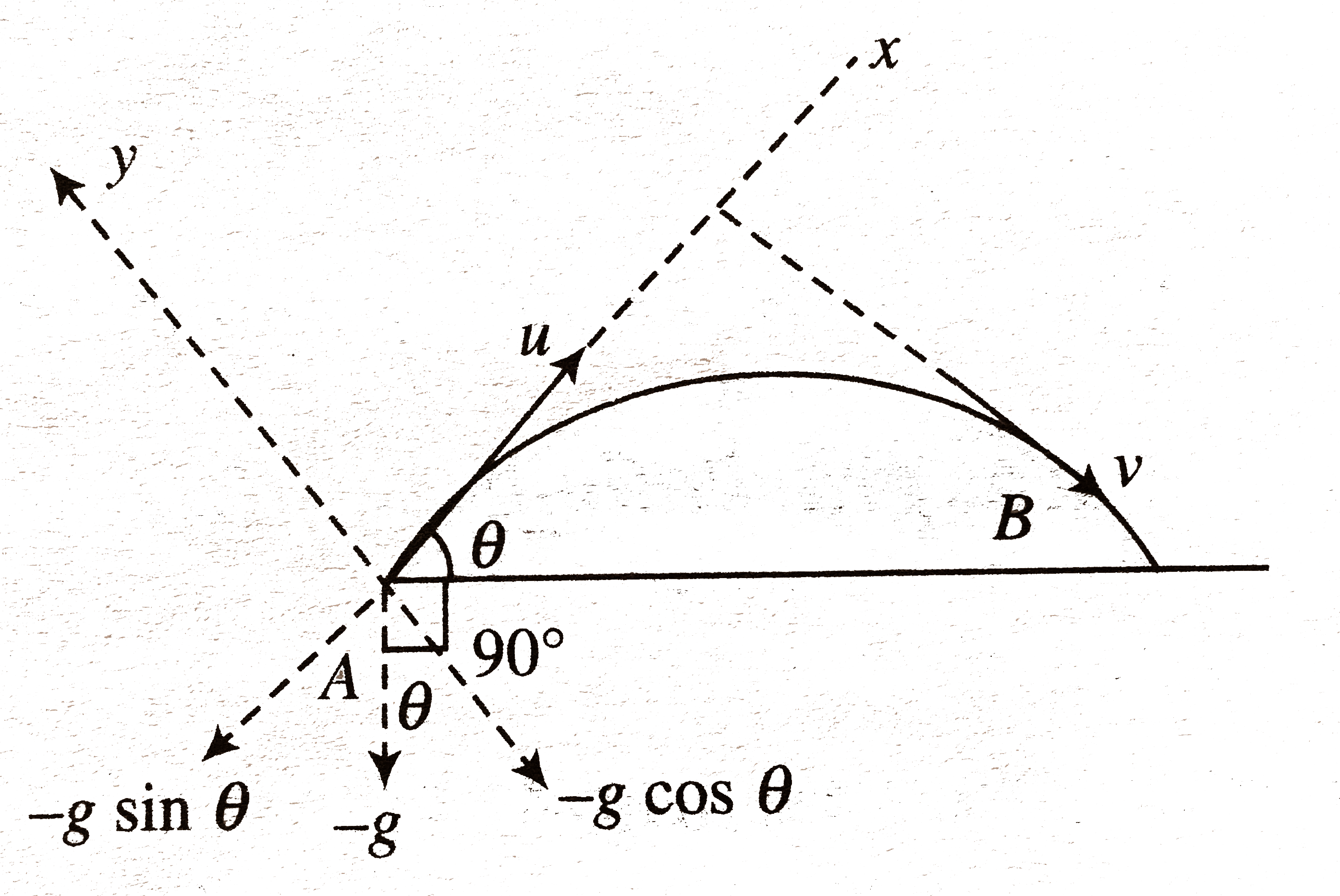
$u^{2} + u . g (- sin θ) t = 0 . t = 0$
So, $t = \frac{u}{g sin θ}$ is the desired time.
To find out the velocity we can use the same relation as used in this question. But as at final position (considered) only the y - component of velocity is present, so we need to use the same relation in y - direction.
$v_{y} = u_{y} + a_{g} t$
$\Rightarrow v = 0 - g . cos θ t$
= $- g cos θ \frac{u}{g sin θ} = - u cot θ$ is the velocity at position $B$ .
.
Method 3 : If the initial velocity $u$ and velocity at time $t$ are perpendicular, then the final velocity will be at an angle $θ$ with the vertical.
The horizontal component of velocity is unchanged throughout the motion . Therefore,
$u cos θ = v sin θ$
or $v = u cot θ$
THe vertical component of velocity after time $t = - v cos θ$ .
From the equation, $v_{y} = u sin θ - g t - v cos θ = u sin θ - g t$
$t = \frac{u sin θ + v cos θ}{g} = \frac{u sin θ + u cot θ cos θ}{g}$
= $\frac{u}{g} [\frac{{sin}^{2} θ + {cos}^{2} θ}{sin θ}] = \frac{u}{g} cos e c θ$
Method 4 : The slope of trajectory at the point of projection, $m_{1} = tan θ$
Slope of trajectory after time $t$ ,
$m_{2} = \frac{d y}{d x} = \frac{d y / d t}{d x / d t} = \frac{v_{y}}{v_{x}} = \frac{u sin θ - g t}{u cos θ}$
Slopes are perpendicular, $(\frac{u sin θ - g t}{u cos θ}) (tan θ) = - 1$
or $t = \frac{u}{g sin θ}$ .

A particle is projected with a velocity u making an angle $θ$ with the horizontal. At any instant its velocity becomes v which is perpendicular to the initial velocity u. Then v is
A $u cos θ$
B $u tan θ$
C $u sec θ$
D $u cot θ$
A particle is projected with velocity $v$ at an angle of $θ$ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
A $\frac{g cos θ}{θ v}$
B $\frac{g}{v sin θ}$
C $\frac{g}{v θ}$
D $\frac{g θ}{v sin θ}$
A particle is projected with velocity v at an angle $θ$ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
A $\frac{g cos θ}{θ v}$
B $\frac{g}{v sin θ}$
C $\frac{g}{v θ}$
D $\frac{g θ}{v sin θ}$