A particle is travelling in a straight line, it has a initial velocity of 10ms−1. When it is subjected to an acceleration of −2ms−2 for 8 sec. find displacement and distance traversed in 8 sec.
To solve the problem, we need to calculate both the displacement and the distance traversed by the particle over a time period of 8 seconds, given its initial velocity and acceleration.
1. Identify the given values:
- Initial velocity (U) = 10 m/s
- Acceleration (a) = -2 m/s² (negative indicates deceleration)
- Time (t) = 8 seconds
2. Calculate the displacement using the equation of motion:
The equation for displacement (S) when initial velocity, acceleration, and time are known is:
S=Ut+12at2
Substituting the values into the equation:
S=(10m/s)×(8s)+12×(−2m/s2)×(8s)2
S=80m+12×(−2)×64
S=80m−64m
S=16m
3. Determine the time taken to come to rest:
To find out how long it takes for the particle to stop, we can use the equation:
V=U+at
Setting final velocity (V) to 0:
0=10+(−2)t
2t=10⟹t=5s
4. Calculate the distance covered until it stops:
We can use the equation:
S=V2−U22a
Substituting V = 0, U = 10 m/s, and a = -2 m/s²:
S=0−(10)22×(−2)
S=−100−4=25m
5. Calculate the distance covered after stopping:
After 5 seconds, the particle stops, and there are 3 seconds left. During this time, it will move back due to the negative acceleration. We can calculate this using:
S=Ut+12at2
Here, U = 0 (it starts from rest), a = 2 m/s² (positive since it's moving in the opposite direction), and t = 3 s:
S=0+12×2×(3)2
S=0+1×9=9m
6. Calculate the total distance traversed:
The total distance is the sum of the distance traveled before stopping and the distance traveled after stopping:
Total Distance=25m+9m=34m
Final Results:
- Displacement: 16 m
- Total Distance Traversed: 34 m
- Initial velocity (U) = 10 m/s
- Acceleration (a) = -2 m/s² (negative indicates deceleration)
- Time (t) = 8 seconds
The equation for displacement (S) when initial velocity, acceleration, and time are known is:
S=Ut+12at2
Substituting the values into the equation:
S=(10m/s)×(8s)+12×(−2m/s2)×(8s)2
S=80m+12×(−2)×64
S=80m−64m
S=16m
To find out how long it takes for the particle to stop, we can use the equation:
V=U+at
Setting final velocity (V) to 0:
0=10+(−2)t
2t=10⟹t=5s
We can use the equation:
S=V2−U22a
Substituting V = 0, U = 10 m/s, and a = -2 m/s²:
S=0−(10)22×(−2)
S=−100−4=25m
After 5 seconds, the particle stops, and there are 3 seconds left. During this time, it will move back due to the negative acceleration. We can calculate this using:
S=Ut+12at2
Here, U = 0 (it starts from rest), a = 2 m/s² (positive since it's moving in the opposite direction), and t = 3 s:
S=0+12×2×(3)2
S=0+1×9=9m
The total distance is the sum of the distance traveled before stopping and the distance traveled after stopping:
Total Distance=25m+9m=34m
- Displacement: 16 m
- Total Distance Traversed: 34 m
Topper's Solved these Questions
- DESCRIPTION OF MOTIONBOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-1
86 Videos
- DESCRIPTION OF MOTIONBOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-2
25 Videos
- DESCRIPTION OF MOTIONBOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-3
34 Videos
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type
13 Videos
Similar Questions
A particle moves in a straight line with constant velocity of 5 ms−1 for 2 sec. it then moves with a constant acceleration of −2ms−2 for 8 sec. draw velocity-time graph for 10 sec of motion and find
(a). Final velocity
(b). Displacement
(c). Total distance.
View SolutionA particle is moving along a straight line.The initial velocity is 10ms and it is , moving with constant retardation of 2ms2 .. The distance travelled by the particle until it comes to rest is
View Solution
Knowledge Check
A particle starts moving in +ve x direction with initial velocity of 10ms−1 with a uniform acceleration of magnitude 2ms−2 but directed in -ve x direction. What is the distance traversed by the particle in 12 seconds:
A−24mB24mC70mD74mA particle has initial velocity of 17ms−1 towards east and constant acceleration of 2ms−2 due west. The distance covered by it in 9th second of motion is :
A0 mB0.5 mC72 mD2 mA particle is moving along straight line with initial velocity +7m/sec and uniform acceleration −2m/sec2 . The distance travlled by the particle in 4th second of its motion is:
A0B0.25mC0.5mD7m
[" A particle is moving "],[" along a straight line.The "],[" initial velocity is "10m/s],[" and it is moving with "],[" constant reterdation of "],[2m/s^(2)" .The distance "],[" travelled by the particle "],[" until it comes to rest is "]
View SolutionA particle moves with a constant acceleration a=2ms−2 along a straight line. If it moves with an initial velocity of 5ms−1, then obtain an expression for its instantaneous velocity.
View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is s=12m.
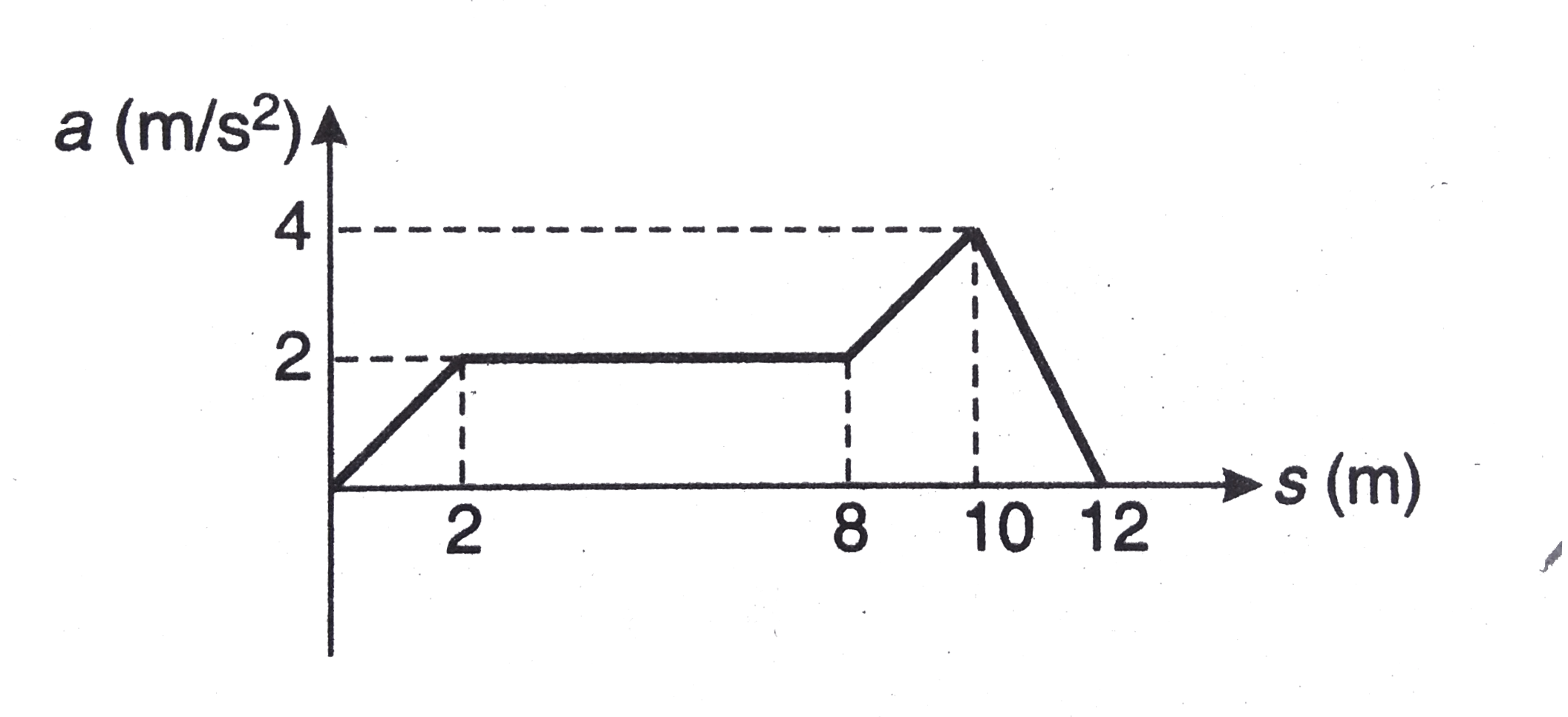
View SolutionA particle has an initial velocity (6ˆi+8ˆj)ms−1 and an acceleration of (0.8ˆi+0.6ˆj)ms−2. Its speed after 10s is
View SolutionA particle has an initial velocity of 5.5ms−1 due east and a constant acceleration of 1ms−2 due west. The distance covered by the particle in sixth second of its motion is.
View Solution
