A particle moves aling x-axis with an initial speed v0=5ms−1. If its acceleration varies with with time asshown in a−t graph in .
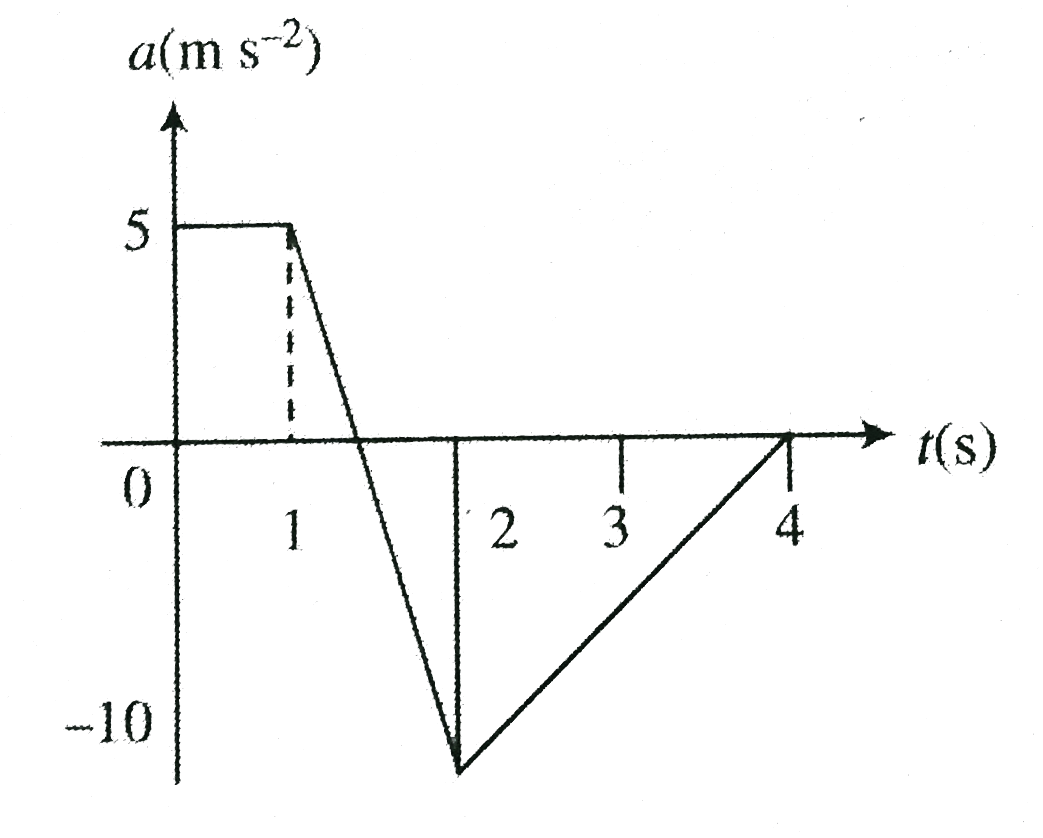 .
.
a. Find the .
The velocity of the particle at t=4s can given as
→v4=→v0+Δ→v …(i)
where Δ→v≡A
(=area under a−t graaph during four seconds )
Referring to a−t graph , we have
A=A1+A2−A3−A4 ....(ii)
where A1=5×1=5,A2=12×x×5,
A3=12×(−1−x)×10, and A4=12×2×10=10
We can find x as following:
Using properties of similar triangles, we have x5=1−x10
This yields x=12.
 .
.
Substituting x=12∈A2=12×x×5
and A3=12(1−x)×10,
we have A2=−56 and A3=103.
Then substitution A1,A2,A3, and A4 in (ii), we have A=−7.5.
Negative area tells us that change in velcity is along −x direction
Δ→v=−7.5ms−1
Hence, substituting (i),
→v0=5ms−1 and Δ→v=−7.5ms−1,
we have
→v4=→v0+Δ→v=5−7.5=−2.5ms−1.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Solved Examples9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.117videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer9videos
KINEMATICS-2
Similar Questions
A particle moves vertically with an upwards initial speed v0=10.5ms−1. If its acceleration varies with time as shown in a-t graph in figure, find the velocity of the particles at t = 4s.
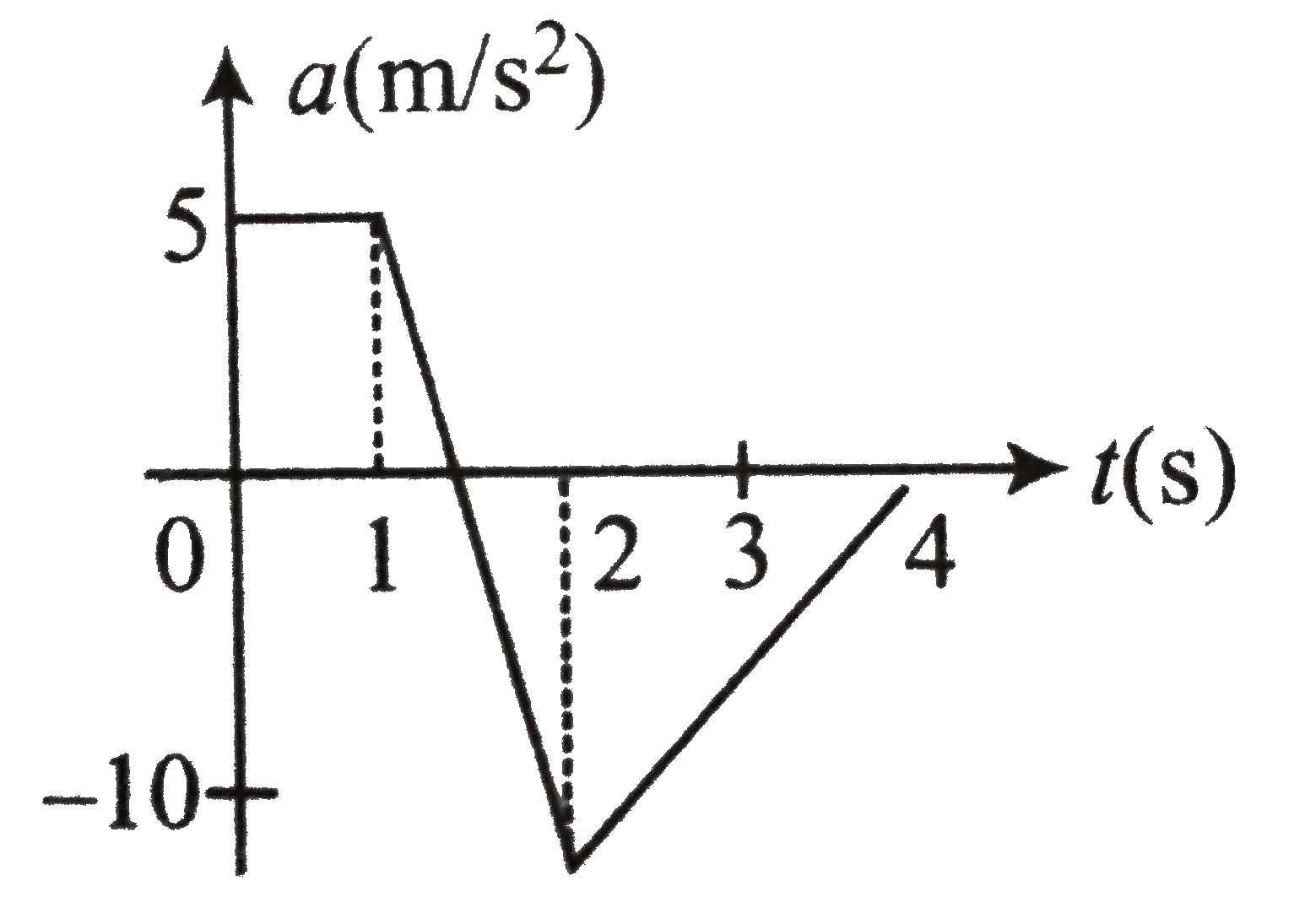 View Solution
View SolutionA particle moves vertically with an upward initial speed v0=5m/s. If its acceleration varies with time as shwon in a−t graph in the fig. 4.30, find the velocity of the particle at t=7s.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle moves along x-axis in such a way that its r-coordinate varies with time't according to the equation x= (8−4t+6t2) metre. The velocity of the particle will vary with time according to the graph
A B
B C
C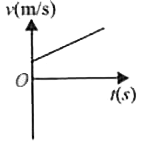 D
D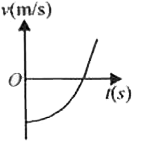
- Question 2 - Select One
A particle moves along x - axis in such a way that its x - co - ordinate varies with time according to the equation x=4−2t+t2. The speed of the particle will vary with time as
A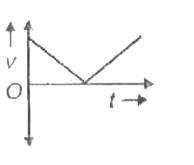 B
B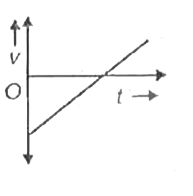 C
C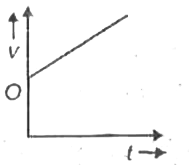 D
D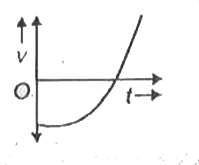
- Question 3 - Select One
A particle moves along x-axis and its acceleration at any time t is a = 2 sin (πt), where t is in seconds and a is in m/s2 . The initial velocity of particle (at time t = 0) is u = 0.
Q. Then the distance travelled (in meters) by the particle from time t = 0 to t = 1 s will be :A2πB1πC4π4Dnone of these
A particle is projected up with initial speed u=10ms−1 from the top of a building at time t=0. At time t=5s the particle strikes the ground. Find the height of the building in meter.
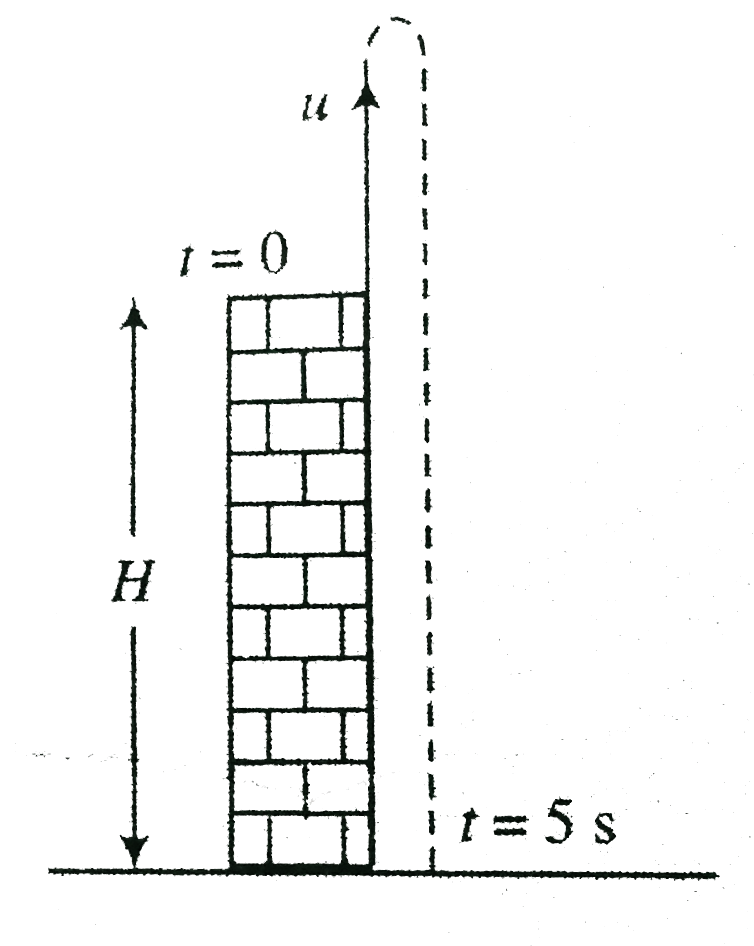 .View Solution
.View Solution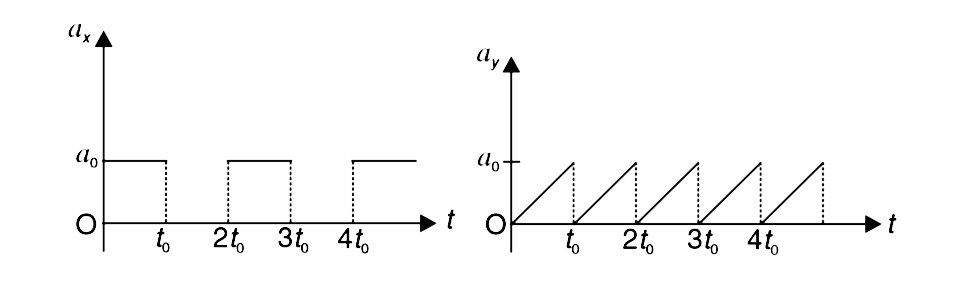
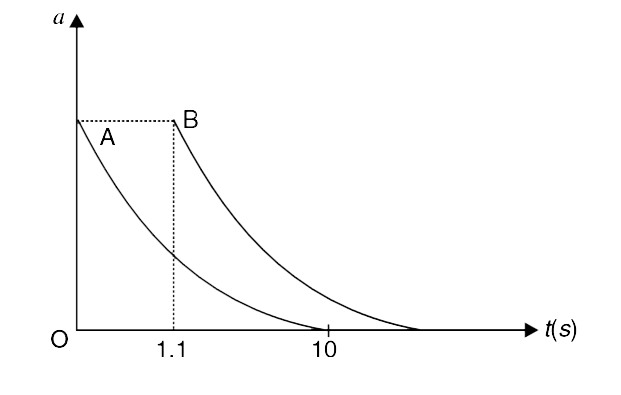
A particle is moving in x–y plane. The x and y components of its acceleration change with time according to the graphs given in figure. At time t=0, its velocity is v0 directed along positive y direction. if a0=v0t0, find the angle that the velocity of the particle makes with x axis at time t=4t0.View SolutionParticle A starts from rest and moves along a straight line. Acceleration of the particle varies with time as shown in the graph. In 10 s the velocity of the particle becomes 60m/s and the acceleration drops to zero. Another particle B starts from the same location at time t=1.1s and has acceleration – time relationship identical to A with a delay of 1.1s. Find distance between the particles at time t=15s.
 View Solution
View SolutionA particle moves along x-axis in such a way that its x-coordinate varies with time t according to the equation x=(8−4t+6t2) metre.
The velocity of the particle will vary with time according to the graph :-View SolutionA particle moves along x-axis and its acceleration at any time t is a = 2 sin (πt), where t is in seconds and a is in m/s2 . The initial velocity of particle (at time t = 0) is u = 0.
Q. Then the magnitude of displacement (in meters) by the particle from time t = 0 to t = t will be :View Solution

